Je résous des problèmes

Le cahier de maths de Céline a 96 pages. Elle utilise son cahier pour noter son cours et pour faire ses exercices. Elle écrit une demi-page de cours et une page d'exercices par heure de cours de maths. Elle a 3 h 30 de cours de maths par semaine.

1. Combien de pages utilise-t elle en une semaine ? En x heures ?

2. Une année de cours compte 36 semaines. Céline aura-t-elle assez de place dans son cahier ?

Dans la forme d'un nautile se cache une régularité mathématique. On peut reproduire la forme d'un nautile à l'aide d'une figure dont toutes les parties sont des carrés auxquels on ajoute des quarts de cercle.

1. Reproduisez cette spirale.


2. Quelle est la longueur du côté du carré violet si celle du carré vert est de x cm ?

1. Combien d'hexagones faut-il ajouter pour obtenir l'étape suivante ?

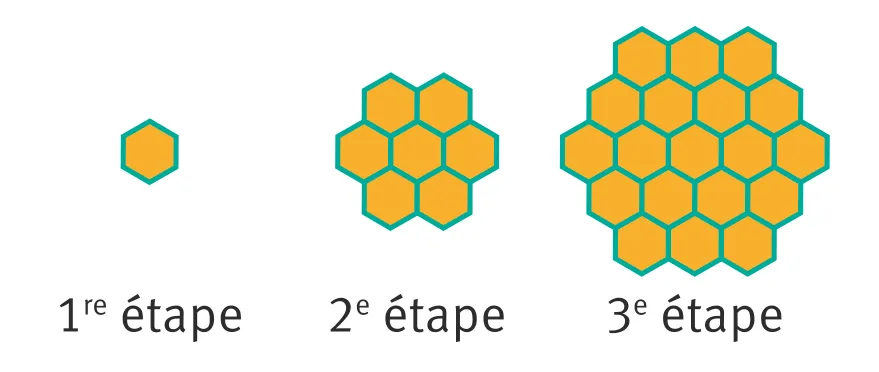
2. Combien d'hexagones y a-t-il dans le dessin de la 4^{\text{e}} étape ?

Mme Dory a deux enfants. Cette année l'un est deux fois plus vieux que l'autre. Tous les mois, chacun reçoit le double de son âge en euros comme argent de poche.

1. Donnez une expression littérale qui corresponde à l'argent que Mme Dory donne chaque mois à ses enfants.

2. Donnez une expression littérale qui correspond à l'argent que Mme Dory donnera chaque mois aux deux enfants l'année prochaine.

La figure montre un solide formé de 6 faces triangulaires. On écrit un nombre à chaque sommet. Deux nombres, 1 et 5, sont déjà placés.

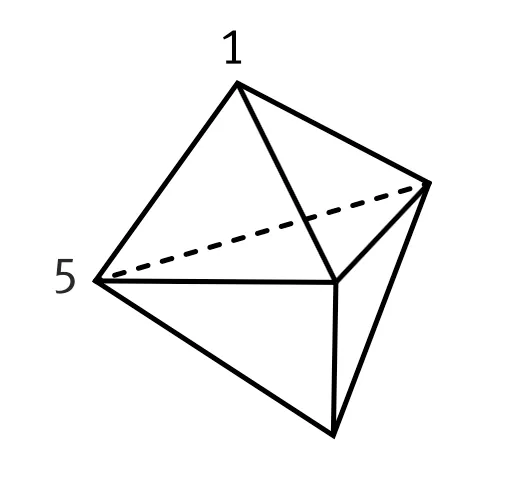
1. Placez 3 autres nombres tels que les sommes des 3 nombres aux sommets de chacune des faces soient égales.

Christian veut construire un enclos en forme de rectangle pour ses canards. Dans son garage, il a trouvé 8 m de clôture et il y a un long mur dans son jardin. Il a une bonne idée : « Si j'utilise le mur comme limite de mon enclos, j'économise la clôture pour ce côté ! » Christian a calculé qu'il lui reste 5 m pour la longueur de l'enclos s'il choisit une largeur de 1,5 m.

1. Validez le calcul de Christian.

2. Il se demande si l'aire de l'enclos sera plus grande s'il choisit une autre largeur. Complétez le tableau.


3. Christian introduit la variable x pour la largeur de l'enclos. Exprimez la longueur du côté parallèle au mur en fonction de x. Exprimez l'aire de l'enclos en fonction de x.

4. Christian pense que le plus efficace serait de construire l'enclos en forme de carré. Expliquez le plus précisément possible pourquoi il se trompe.

On forme un rectangle de longueur 3 allumettes et de largeur 1 allumette que l'on agrandit pas à pas en ajoutant à chaque étape une allumette à chacun de ses côtés.

1. Représentez l'étape 4.


2. Quel est le nombre d'allumettes dont on a besoin pour construire un rectangle de 30 allumettes de largeur ?

3. Donnez une expression littérale qui exprime le nombre d'allumettes dont on a besoin pour construire un rectangle de largeur n allumettes.

Position initiale : Former un triangle avec 3 allumettes.  1re étape : Ajouter 2 allumettes à gauche et 2 allumettes à droite pour obtenir 3 triangles.  2e étape : Ajouter 2 allumettes à gauche et 2 allumettes à droite pour obtenir 5 triangles, etc.

1. Combien d'allumettes faut-il pour conclure 9 étapes ?

2. Combien d'étapes peut-on terminer avec 100 allumettes ?

3. Combien d'allumettes faut-il pour former 33 triangles ?

1. Calculez la surface d'un parallélépipède rectangle dont les longueurs des arêtes sont 7 cm ; 2,2 cm et 4 cm. Conseil : dessinez d'abord un patron.

2. Exprimez la surface d'un parallélépipède rectangle en fonction de la longueur de ses arêtes.

1. Le carré vert de la position initiale est de côté x. Exprimez l'aire de la surface verte dans la 2e étape à l'aide d'une expression littérale.

2. Faites un dessin correspondant à la prochaine étape et exprimez l'aire de la nouvelle surface verte à l'aide d'une expression littérale.

3. Calculez l'aire de la surface verte pour un tapis de côté 3 m dans la 3e étape.

Il est possible de voir sur toutes les autoroutes de France les panneaux ci-contre.Ces panneaux indiquent quʼil faut laisser au moins deux traits de signalisation de la bande dʼarrêt dʼurgence entre son véhicule et celui qui nous précède.

1. Expliquez pourquoi il est nécessaire de respecter ce conseil, et donnez une formule générale donnant la distance de sécurité que toute voiture doit respecter sur sol sec, quelle que soit sa vitesse.