Chapitre 9
Problèmes résolus
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32Un jeu de hasard
✔ Je modélise une situation à l'aide d'un schéma, d'un tableau ou d'un arbre
✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème
Julian lance une pièce puis pioche une boule dans une urne qui contient 2 boules vertes, 1 rouge et 3 bleues. Quelle est la probabilité quʼil nʼait pas obtenu pile ni tiré la boule verte ?
✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème
Julian lance une pièce puis pioche une boule dans une urne qui contient 2 boules vertes, 1 rouge et 3 bleues. Quelle est la probabilité quʼil nʼait pas obtenu pile ni tiré la boule verte ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1
Pour calculer une probabilité en situation d'équiprobabilité, on peut dessiner un arbre qui présente tous les évènements susceptibles de se produire. Ensuite, on regarde le nombre dʼissues pour lesquelles lʼévènement recherché se produit et on le divise par le nombre total dʼissues.
Corrigé 1
On peut tracer lʼarbre suivant.

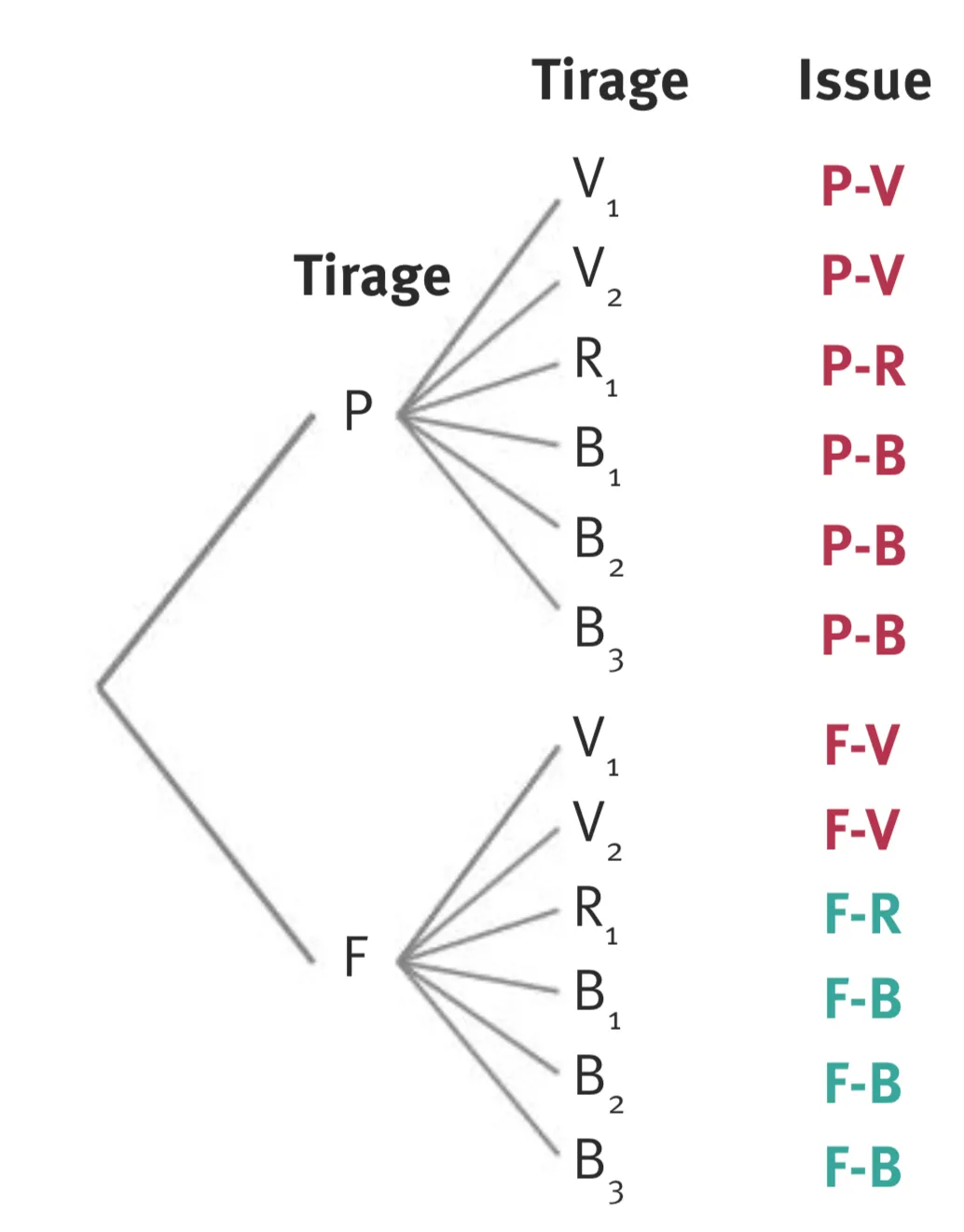


- La situation est symétrique : on pourrait échanger les deux côtés de la pièce ou les deux boules. On est donc dans une situation dʼéquiprobabilité.
- Il y a donc 4 issues où Julian nʼa eu ni pile ni la boule verte sur un total de 12 issues.
La probabilité de ne tirer ni pile ni la boule verte est donc de \bold{\dfrac{4}{12}} soit \bold{\dfrac{1}{3}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2
Pour calculer une probabilité, on peut également commencer par calculer la probabilité de son évènement contraire, pour ensuite la calculer elle-même.
\text{P(A)} = 1 - \dfrac{2}{3}
\bold{\textbf{P(A)} = \dfrac{1}{3}}
Corrigé 2
- Le contraire de lʼévènement A « Ne tirer ni un pile ni une boule verte » est lʼévènement : « Tirer une boule verte ou avoir un pile (ou avoir pile et une boule verte) ». Le nombre dʼissues de cet évènement est 8 sur un total de 12 issues. Donc \text{P(}\overline{\text{A}}) = \dfrac{8}{12} = \dfrac{2}{3}.
- Or on sait que \text{P(A)} + \text{P(}\overline{\text{A}}\text{)} = 1 donc
\text{P(A)} = 1 - \dfrac{2}{3}
\bold{\textbf{P(A)} = \dfrac{1}{3}}
Il ne faut pas compter plusieurs fois l'évènement « Tirer pile et tirer une boule verte ».
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problème similaireVoir p. 206 : Coffre-fort.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

