Chapitre 9
Problèmes résolus
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33Jeu de dupes ?
✔ Je sais passer du langage naturel au langage mathématiques et inversement
✔ Je comprends et j'utilise une simulation informatique
Paul propose à Mathieu un nouveau jeu : ils vont choisir ensemble un nombre et celui-ci déterminera le nombre de tours quʼils feront. À chaque tour, Mathieu lancera deux pièces équilibrées et Paul lancera deux dés puis sommera les résultats des deux dés. Paul gagne sʼil a obtenu plus de fois 7 que Mathieu de doubles faces. Sinon, la victoire revient à Mathieu.
Mathieu devrait-il jouer ?
✔ Je comprends et j'utilise une simulation informatique
Paul propose à Mathieu un nouveau jeu : ils vont choisir ensemble un nombre et celui-ci déterminera le nombre de tours quʼils feront. À chaque tour, Mathieu lancera deux pièces équilibrées et Paul lancera deux dés puis sommera les résultats des deux dés. Paul gagne sʼil a obtenu plus de fois 7 que Mathieu de doubles faces. Sinon, la victoire revient à Mathieu.
Mathieu devrait-il jouer ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1
Pour savoir si un pari ou un jeu est intéressant, il faut calculer la probabilité de gain de chacun des joueurs. Pour cela, il est possible de construire un tableau qui récapitule toutes les issues possibles, à partir duquel on va calculer les probabilités.
Nous sommes en situation dʼéquiprobabilité : par symétrie, les faces des pièces ont autant de chances dʼapparaitre lʼune que lʼautre.
Sur les 4 issues du tableau, il nʼy en a quʼune qui correspond à « Tirer face deux fois ». Donc \text{P(FF)} = \dfrac{1}{4}.
Pour Paul, on construit un tableau avec les nombres de 1 à 6 sur la première ligne et la première colonne ; chaque case est la somme du nombre de sa ligne et de sa colonne, comme dans le tableau de lʼexercice 30 p. 203. La probabilité d'avoir 7 est donc :
Corrigé 1
- Les issus pour Mathieu sont :
| Côté obtenu | Pile | Face |
| Pile | Pile-Pile | Pile-Face |
| Face | Face-Pile | Face-Face |
Sur les 4 issues du tableau, il nʼy en a quʼune qui correspond à « Tirer face deux fois ». Donc \text{P(FF)} = \dfrac{1}{4}.
Pour Paul, on construit un tableau avec les nombres de 1 à 6 sur la première ligne et la première colonne ; chaque case est la somme du nombre de sa ligne et de sa colonne, comme dans le tableau de lʼexercice 30 p. 203. La probabilité d'avoir 7 est donc :
- \text{P}(\text{faire }7) = \dfrac{\text{nombre de 7 dans le tableau}}{\text{nombre de cases dans le tableau}}
- \text{P}(\text{faire }7) = \dfrac{6}{36}
- \text{P(faire }7) = \dfrac{1}{6}
Puisque \dfrac{1}{4} \ge \dfrac{1}{6}, la probabilité que Mathieu ait deux faces est plus importante que la probabilité que Paul ait un 7.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2
Pour calculer la probabilité de gain de chacun des joueurs, on peut utiliser un tableur pour faire une simulation du jeu sur un très grand nombre dʼessais. Cela permettra de voir lequel des joueurs a le plus de chances de gagner.
Corrigé 2
On simule 800 tirages dʼun nombre aléatoire avec la formule =ALEA.ENTRE.BORNES(borne minimale ; borne maximale).
Pour déterminer le nombre de fois que lʼon a une valeur parmi nos simulations, il faut entrer la formule =NB.SI(plage de nos simulations ; nombre recherché parmi celles-ci).

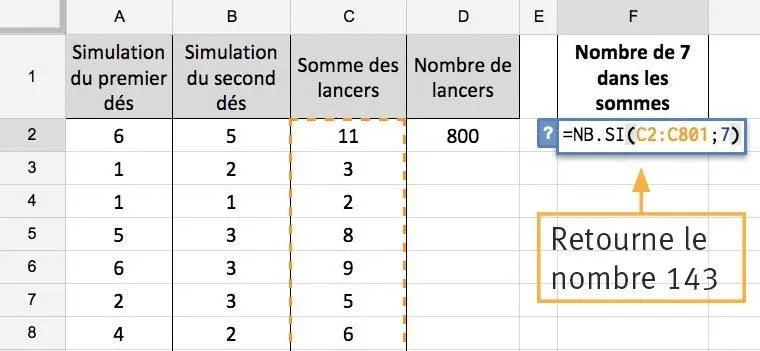 La probabilité qu'il y ait donc \dfrac{143}{800} \approx \dfrac{1}{6}.
La probabilité qu'il y ait donc \dfrac{143}{800} \approx \dfrac{1}{6}.
Or \frac{1}{6}\lt\frac{1}{4}.
Mathieu devrait donc accepter de jouer.
Pour déterminer le nombre de fois que lʼon a une valeur parmi nos simulations, il faut entrer la formule =NB.SI(plage de nos simulations ; nombre recherché parmi celles-ci).
- Après une première simulation, on obtient 202 fois face-face. La probabilité que Mathieu ait face-face est donc dʼenviron \dfrac{202}{800} \approx \dfrac{1}{4}.
- Pour Paul, nous obtenons alors :


Or \frac{1}{6}\lt\frac{1}{4}.
Mathieu devrait donc accepter de jouer.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problème similaireVoir p. 34 : Jeu de hasard.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

