Mathématiques Cycle 4
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 9
J'apprends
Probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ADécouvrir les probabilités
Je découvre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Expérience aléatoire et évènement
Définition
Une expérience aléatoire est une expérience, reproductible, dont on connait tous les résultats possibles sans pouvoir déterminer de manière certaine lequel va se produire.
On appelle « issue » ou « éventualité » de lʼexpérience chacun des résultats possibles de lʼexpérience aléatoire.
On appelle « issue » ou « éventualité » de lʼexpérience chacun des résultats possibles de lʼexpérience aléatoire.
Exercices n° p. 198-201
J'applique
Consigne :
Jouer à pile ou face, est-ce une expérience aléatoire ?
Correction :
Jouer à pile ou face nʼa que deux issues : tomber sur pile ou tomber sur face. On en connait tous les résultats possibles, donc le jeu de pile ou face est bien une expérience aléatoire.
Définition
Un évènement est constitué dʼun ensemble dʼissues. Il peut être ou ne pas être réalisé lors dʼune expérience aléatoire. Un évènement est réalisé lorsquʼon obtient lʼune des issues qui le composent.
Exercices n° p. 198-201
J'applique
Consigne :
On lance un dé à six faces. Proposez un évènement à une issue, à deux issues, à trois issues. Proposez un évènement qui nʼa aucune issue.
Correction :
- « Obtenir un 6 » est un évènement à une issue, car il nʼy a quʼune face du dé marqué dʼun 6 dessus.
- « Obtenir 1 ou 3 » est un évènement à deux issues.
- « Obtenir un nombre pair » est un évènement à trois issues, car 2, 4 et 6 sont des nombres pairs.
- « Obtenir un 8 » est un évènement à zéro issue, car il nʼy a pas de 8 sur un dé à six faces.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Évènements particuliers
Définition
Évènement impossible : un évènement qui ne peut se réaliser, qui nʼest constitué dʼaucune issue.
Évènement certain : un évènement qui se réalise toujours, qui est constitué de toutes les issues.
Évènements incompatibles : deux évènements qui ne peuvent se réaliser lors de la même expérience, qui nʼont aucune issue en commun.
Évènement contraire : lʼévènement contraire de \text{A} est lʼévènement qui se réalise lorsque A ne se réalise pas. Il est constitué des issues qui ne sont pas dans A et on le note \text{A} , ce qui se prononce « le contraire de \text{A} ».
Évènement certain : un évènement qui se réalise toujours, qui est constitué de toutes les issues.
Évènements incompatibles : deux évènements qui ne peuvent se réaliser lors de la même expérience, qui nʼont aucune issue en commun.
Évènement contraire : lʼévènement contraire de \text{A} est lʼévènement qui se réalise lorsque A ne se réalise pas. Il est constitué des issues qui ne sont pas dans A et on le note \text{A} , ce qui se prononce « le contraire de \text{A} ».
Exercices n° p. 198-201
J'applique
Consigne :
On place une boule rouge et deux boules bleues dans un sac, puis on en tire une au hasard. Donnez un exemple pour chacun des évènements particuliers évoqués dans le cours.
Correction :
- Évènement impossible : « Tirer une boule verte », car il nʼy en a pas dans le sac.
- Évènement certain : « Tirer une boule bleue ou rouge », car il nʼy a que ces deux couleurs dans le sac.
- Évènements incompatibles : « Tirer une boule rouge » et « Tirer une boule bleue » sont des évènements incompatibles, car on ne tire quʼune seule boule à la fois.
- Évènement contraire : « Tirer une boule rouge » est lʼévènement contraire de « Tirer une boule bleue », et inversement. Comme il nʼy a que ces deux couleurs, si on ne tire pas une couleur, cʼest que lʼon tire lʼautre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BCalcul de probabilités
Je découvre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Probabilité dʼune issue
Définition
La probabilité dʼune issue représente les chances quʼelle apparaisse lors dʼune expérience aléatoire. Cʼest un nombre compris entre 0 et 1. Dans le cas où toutes les issues ont la même probabilité dʼapparaitre, on parle de situation dʼéquiprobabilité. En situation dʼéquiprobabilité, la probabilité de chacune des issues est égale à \dfrac{1}{\text{nombre total d'issues}}.
Exercices n° p. 201-203
Aide
La somme des probabilités de toutes les issues dʼune expérience est égale à 1.
J'applique
Consigne :
On lance un dé à six faces non truqué.
Est-ce une situation dʼéquiprobabilité ? Si oui, quelle est la probabilité de tirer un 5 ?
Correction :
Le dé nʼest pas truqué. On a donc la même probabilité de tirer chacune des six faces. Il y a six issues possibles, donc la probabilité de tirer un 5 est \dfrac{1}{6}.
Remarque :
- On peut écrire une probabilité de trois façons :
- sous forme de nombre décimal : la probabilité de tirer pile est \text{0,5} ;
- sous forme de fraction : la probabilité de tirer pile est de \dfrac{1}{2} ;
- sous forme de pourcentage : on a 50~\% de chance de tirer pile.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Probabilité dʼun évènement
Définition
La probabilité dʼun évènement \text{A} est la somme des probabilités des issues qui le réalisent. On note cette probabilité P(A).
Exercices n° p. 201-203
J'applique
Consigne :
On lance un dé truqué, dont on donne les probabilités de tirer chaque face.
| Face | 1 | 2 | 3 | 4 | 5 | 6 |
| Probabilité | 10% | 10% | 10% | 20% | 20% | 30% |
Quelle est la probabilité de tirer un nombre pair ?
Correction :
Cʼest la probabilité de tirer 2 (soit 10 %), 4 (soit 20 %) ou 6 (soit 30 %). La probabilité de tirer un nombre pair est donc 10 % + 20 % + 30 % = 60 %.
Propriété
En situation dʼéquiprobabilité, on a :
\text{P(A)} = \dfrac{\text{nombre d'issues pour lesquelles est réalisé}}{\text{nombre total d'issues}}
\text{P(A)} = \dfrac{\text{nombre d'issues pour lesquelles est réalisé}}{\text{nombre total d'issues}}
Exercices n° p. 201-203
Aide
Avant d'utiliser cette formle, il faut toujours vérifier qu'on est en situation d'équiprobabilité.
J'applique
Consigne :
Lorsque lʼon lance un dé à huit faces non truqué, quelle est la probabilité de lʼévènement A, « Tirer un nombre strictement inférieur à 3 » ?
Lorsque lʼon lance un dé à huit faces non truqué, quelle est la probabilité de lʼévènement A, « Tirer un nombre strictement inférieur à 3 » ?
Correction :
Le dé est non truqué, donc nous sommes dans une situation dʼéquiprobabilité. Le dé a huit faces, donc il y a huit issues possibles. Il y a deux issues qui réalisent lʼévènement : tirer 1 ou 2.
Donc \text{P(A)} = \dfrac{2}{8} = \dfrac{1}{4} = 0\text{,}25 = 25%
Le dé est non truqué, donc nous sommes dans une situation dʼéquiprobabilité. Le dé a huit faces, donc il y a huit issues possibles. Il y a deux issues qui réalisent lʼévènement : tirer 1 ou 2.
Donc \text{P(A)} = \dfrac{2}{8} = \dfrac{1}{4} = 0\text{,}25 = 25%
Propriété
Si un évènement A est certain, alors \text{P(A)} = 1.
Si un évènement A est impossible, alors \text{P(A)} = 0.
Si un évènement A est impossible, alors \text{P(A)} = 0.
Exercices n° p. 201-203
Exemple :
On tire un dé à six faces.
La probabilité de tirer un entier est 1.
La probabilité de tirer 8 est 0.
On tire un dé à six faces.
La probabilité de tirer un entier est 1.
La probabilité de tirer 8 est 0.
Propriétés
Si deux évènements A et B sont incompatibles, la probabilité que lʼun ou lʼautre se réalise est la somme de leurs probabilités : \text{P(A ou B)} = \text{P(A)} + \text{P(B)}.
Exercices n° p. 202-203
Exemple :
On tire un dé à 6 faces. On note
A : « Tirer 1 ou 2 » et B : « Tirer 4, 5 ou 6 ».
Nous sommes dans une situation dʼéquiprobabilté.
On a \text{P}(\text{A}) = \dfrac{2}{6} = \dfrac{1}{3} et \text{P}(\text{B}) = \dfrac{3}{6} = \dfrac{1}{2}.
A et B sont incompatibles, lʼévènement « A ou B » correspond à « tirer 1, 2, 4, 5 ou 6 ». On a bien \text{P}(\text{A}) = \dfrac{5}{6} = \dfrac{2}{6} + \dfrac{3}{6} = \text{P}(\text{A}) + \text{P}(\text{B})
On tire un dé à 6 faces. On note
A : « Tirer 1 ou 2 » et B : « Tirer 4, 5 ou 6 ».
Nous sommes dans une situation dʼéquiprobabilté.
On a \text{P}(\text{A}) = \dfrac{2}{6} = \dfrac{1}{3} et \text{P}(\text{B}) = \dfrac{3}{6} = \dfrac{1}{2}.
A et B sont incompatibles, lʼévènement « A ou B » correspond à « tirer 1, 2, 4, 5 ou 6 ». On a bien \text{P}(\text{A}) = \dfrac{5}{6} = \dfrac{2}{6} + \dfrac{3}{6} = \text{P}(\text{A}) + \text{P}(\text{B})
Propriété
La somme des probabilités dʼun évènement A et de son contraire vaut 1, soit \text{P(A)} + \text{P}(\overline{\text{A}}) = 1.
Exercices n° p. 201-203
Exemple :
Le contraire de A est \overline{\text{A}} : « Tirer 3, 4, 5 ou 6 ».
On a bien \text{P}(\overline{\text{A}}) = \dfrac{4}{6} = 1 - \dfrac{2}{6} = 1 - \text{P(A)}.
Le contraire de A est \overline{\text{A}} : « Tirer 3, 4, 5 ou 6 ».
On a bien \text{P}(\overline{\text{A}}) = \dfrac{4}{6} = 1 - \dfrac{2}{6} = 1 - \text{P(A)}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CFréquences et probabilités
J'approfondis
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
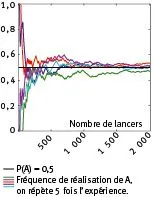
Méthode
On répète de nombreuses fois une expérience aléatoire et lʼon considère la série statistique des résultats.
La fréquence dʼapparition dʼune issue ou dʼun évènement va alors se rapprocher de sa probabilité.
La fréquence dʼapparition dʼune issue ou dʼun évènement va alors se rapprocher de sa probabilité.
On tire un dé équilibré à quatre faces.
Les probabilités de réalisation des faces sont :
| Face | 1 | 2 | 3 | 4 |
| Probabilité | 25 % | 25 % | 25 % | 25 % |
La probabilité de lʼévènement A : « Obtenir 2 ou moins » est donc de 50 %.
Une expérience consiste à lancer le dé 2 000 fois. On répète 5 fois lʼexpérience et on mesure la fréquence de réalisation de lʼévènement A. Les résultats sont consignés dans le tableau et le graphique suivant.
| Face | 1 | 2 | 3 | 4 | Total |
| Effectifs | 2 529 | 2 498 | 2 443 | 2 530 | 10 000 |
| Fréquence | 25,29 % | 24,98 % | 24,43 % | 25,3 % | 100 % |
Fréquence de réalisation de \text{A} : 50,27~\%.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
