Questions Flash / Je m'entraine

Questions FLASH

1

Lequel de ces nombres ne peut pas représenter une probabilité ?

1

×

1,4

0

0,4

2

Lors dʼun lancer de dé, les évènements « Tirer un nombre pair » et « Tirer un 5 » sont...

×

incompatibles.

contraires.

certains.

impossibles.

3

Lors dʼun tirage de cartes dans un jeu, quels sont les évènements réalisés avec une seule issue ?

« Obtenir une figure ».

« Obtenir un pique ».

« Obtenir un as ».

×

« Obtenir un roi de trèfle ».

4

Dans une urne, il y a 15 boules : 3 bleues, 6 jaunes et 6 vertes. Quel est lʼévènement le plus probable ?

×

« Tirer une boule de couleur ».

« Tirer une boule bleue ».

« Tirer une boule jaune ».

« Tirer une boule verte ».

5

Dans la configuration précédente, quel est lʼévènement dont la probabilité vaut 0,2 ?

« Tirer une boule verte ».

×

« Tirer une boule bleue ».

« Tirer une boule jaune ».

« Tirer une boule de couleur ».

6

111 des 185 élèves dʼun collège sont des garçons, donc...

$\dfrac{3}{5}$ des élèves sont des filles.

×

si on choisit un élève au hasard dans le collègen on a 3 chances sur 5 de tomber sur un garçon.

×

les filles représentent 40% de l'effectif du collège.

7

Dans un tirage de cartes, quels sont les évènements incompatibles ?

×

« Tirer un 7 » et « Tirer une figure ».

« Tirer un cœur » et « Tirer un roi ».

« Tirer un carreau » et « Tirer une figure ».

« Tirer un 7 » et « Tirer un nombre ».

Exercice 1 : Donnez au moins deux exemples dʼexpériences aléatoires autres que celles mentionnées dans le cours.

1

Quelles sont les issues possibles pour chacune dʼentre elles ?

2

Êtes-vous sûr quʼil est impossible de prédire lʼissue réalisée ?

Exercice 2 : Donnez toutes les issues possibles des expériences aléatoires suivantes.

1

Une urne contient dix boules numérotées de 1 à 10. On tire une boule de lʼurne.

2

Lors de lʼexpérience précédente, on a tiré la boule n°7. On la met de côté et on procède à un deuxième tirage.

3

On écrit les lettres du mot CACHALOT une à une sur un dé à huit faces et on le lance.

4

On lance une pièce de monnaie équilibrée à trois reprises.

5

On lance un dé équilibré à six faces à deux reprises.

Exercice 3 : A est un évènement aléatoire.

1

Parmi les égalités suivantes, lesquelles représentent des probabilités ?

$\text{P(A)} = 1\text{,}00001$

×

$\text{P(A)} = 1$

×

$\text{P(A)} = 0\text{,}99999999$

$\text{P(A)} = -\dfrac{25}{7}$

×

$\text{P(A)} = \dfrac{4}{5}$

$\text{P(A)} = \dfrac{5}{4}$

Exercice 4 : On lance un dé à six faces.

1

Indiquez si lʼévènement est impossible, certain ou possible.

Exercice 5 : On lance un dé à six faces.

1

Remplissez le tableau avec les nombres dʼissues qui réalisent lʼévènement.

Exercice 6 : On procède à deux lancers successifs dʼun dé à six faces.

1

Remplissez le tableau avec les nombres dʼissues qui réalisent lʼévènement.

Exercice 7 : On écrit chacune des lettres du mot ANACONDA sur les faces dʼun dé à huit faces.

On lance le dé et on regarde la lettre inscrite sur la face supérieure.

1

Quelles sont les issues possibles ? Représentez-les sous forme dʼun arbre.

2

Donnez un exemple dʼévènement composé dʼune unique issue et un exemple dʼévènement composé de plusieurs issues. Justifiez.

3

Lʼévènement « La lettre inscrite sur la face supérieure du dé est B » est-il réalisable ?

4

Combien dʼissues réalisent lʼévènement « La lettre inscrite sur la face supérieure du dé est A » ?

Exercice 8 : Une urne contient trois boules bleues numérotées 1, 2, 3 et quatre boules oranges numérotées 4, 5, 6, 7.

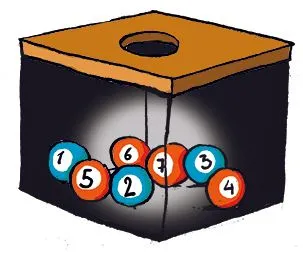
On pioche une boule dans lʼurne.

1

Pour quelles issues lʼévènement « La boule tirée est bleue » est-il réalisé ?

2

Pour quelles issues lʼévènement « Le numéro de la boule tirée est pair » est-il réalisé ?

3

Si la boule tirée est la boule n°5, donnez deux évènements réalisés.

Exercice 9 : Les expériences aléatoires suivantes correspondent-elles à une situation dʼéquiprobabilité ?

1

On sélectionne 8 cartes dans un jeu de 32 cartes. On pioche une carte au hasard parmi ces cartes.

Oui

Non

2

On lance un dé à six faces dont les probabilités dʼapparaitre sont celles indiquées ci-contre :

Non

Oui

3

On pioche une boule au hasard dans une urne qui contient $\dfrac{2}{5}$ de boules vertes et $\dfrac{3}{5}$ de boules bleues.

Non

Oui

4

On lance un palet sur une surface rectangulaire couverte aux $\dfrac{2}{3}$ dʼun tapis vert et pour le reste dʼun tapis bleu.

Oui

Non

Exercice 10 : Vrai ou faux ? Corrigez si nécessaire.

1

Deux évènements contraires sont incompatibles.

2

Deux évènements incompatibles sont forcément contraires.

3

Deux évènements incompatibles peuvent être contraires.

4

$\text{P(évènement certain)} = 1$.

Exercice 11 : Une trousse contient 6 stylos : 2 à pointe large (1 vert, 1 bleu), 4 à pointe fine (1 vert, 2 bleus, 1 rouge). Tous sont indiscernables au toucher.

On en pioche un au hasard. Les évènements suivants sont-ils incompatibles ? Contraires ?

1

Piocher un stylo à pointe fine et piocher un stylo bleu.

Ni incompatibles, ni contraires.

Évènements contraires

Évenèments incompatibles

2

Piocher un stylo vert et piocher un stylo bleu.

Évenèments incompatibles

Évènements contraires

Ni incompatibles, ni contraires

3

Piocher un stylo rouge et piocher un stylo à pointe large.

Évènements contraires

Évenèments incompatibles

Ni incompatibles, ni contraires

4

Piocher un stylo à pointe fine et piocher un stylo à pointe large.

Évènements contraires

Évenèments incompatibles

Ni incompatibles, ni contraires.

5

Piocher un stylo rouge ou bleu et piocher un stylo vert.

Évènements contraires

Ni incompatibles, ni contraires

Évenèments incompatibles

Exercice 12 : On lance un dé à six faces et on sʼintéresse au nombre inscrit sur la face supérieure du dé.

Donnez lʼévènement contraire des évènements suivants :

1

On obtient 5.

2

On obtient 4 ou 5.

3

On obtient un nombre strictement inférieur à 5.

4

On obtient un nombre supérieur ou égal à 2.

5

On obtient au moins 3.

Exercice 13 : Samir joue aux échecs contre son ordinateur.

Il gagne dans la plupart des cas.

1

Laquelle des affirmations suivantes est ici vérifiée ?

Samir a déjà perdu deux parties dʼaffilée. Il gagnera donc forcément la suivante.

×

Samir peut gagner dix parties dʼaffilée.

La probabilité de gagner une partie dépend de lʼissue de la partie précédente.

Exercice 14 : On met des boules de billard anglais dans une urne et on procède à un tirage au hasard.

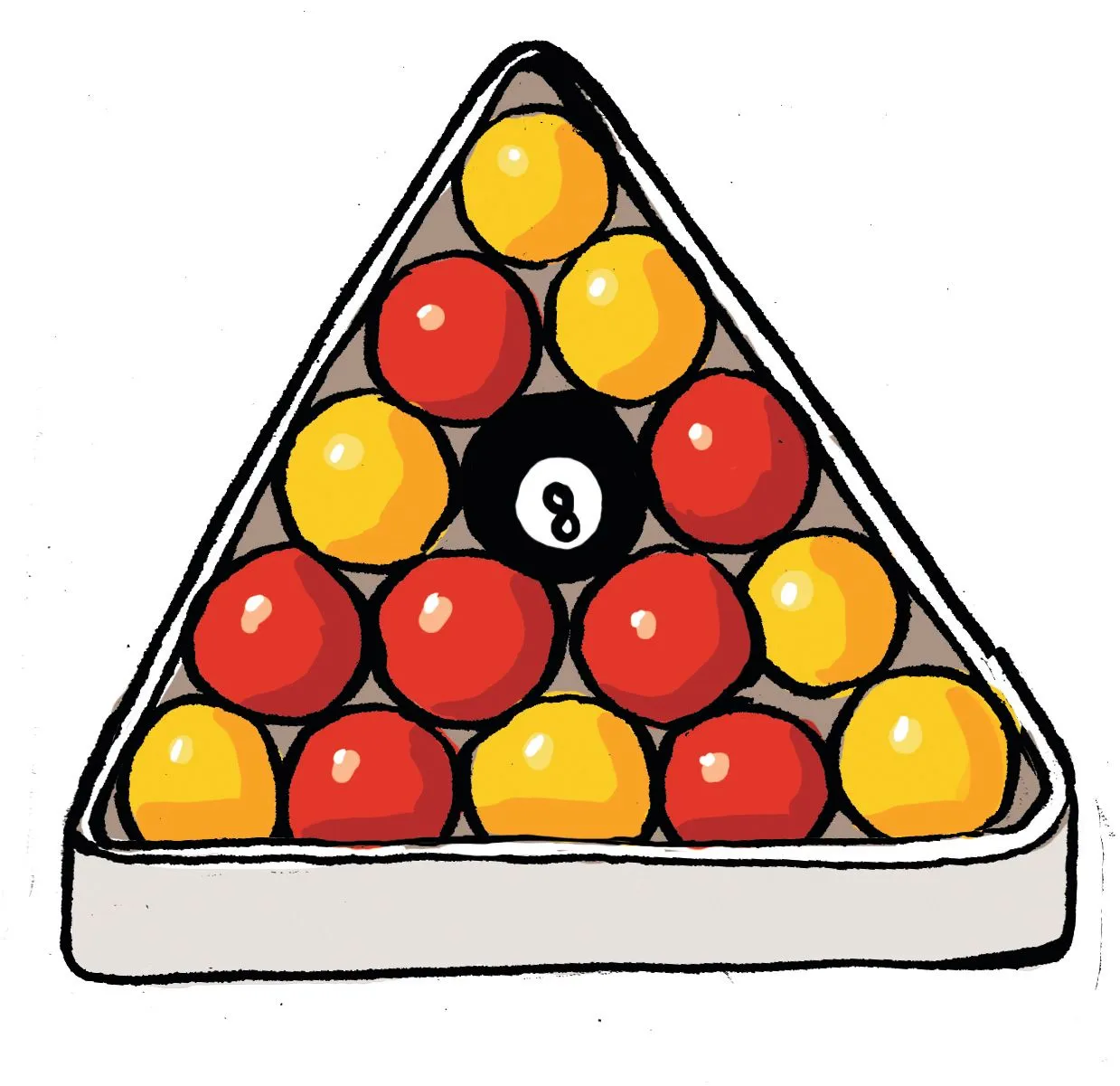
1

On sʼintéresse à la couleur de la boule. Combien dʼissues cette expérience aléatoire a-t-elle ?

2

Définissez un évènement impossible, un évènement certain et un évènement élémentaire.

Exercice 15 : On considère un jeu de 32 cartes dans lequel on tire deux cartes au hasard.

1

Quel est le contraire des évènements suivants ?

2

Combien dʼissues constituent ces évènements contraires ? Choisissez parmi les solutions proposées.

Exercice 16 : On effectue trois lancers successifs dʼune pièce équilibrée et on sʼintéresse à la face supérieure de la pièce.

Représentez par un arbre ou un schéma lʼensemble des issues qui constituent les évènements suivants. Puis, pour chacun, donnez lʼévènement contraire.

1

Tous les lancers donnent pile.

2

Aucun lancer ne donne face.

3

On obtient au moins 2 fois face.

4

On obtient un unique pile.

5

On obtient au plus 3 fois pile.

6

On obtient pile, puis face, puis pile.

7

Un seul des lancers donne pile.

8

On obtient pile ou face à chaque lancer.

Exercice 17 : Une roue de loterie compte huit secteurs de taille identique.

1

Quelle est la probabilité que la roue ne tombe pas sur le secteur vert ?

Exercice 18 : Une urne contient des jetons verts, bleus et rouges.

La probabilité de tirer un jeton vert de lʼurne est de $\dfrac{1}{ 3}$ et la probabilité de tirer un jeton rouge de $\dfrac{2}{ 5}$.

1

Quelle est la probabilité de tirer un jeton bleu ?

2

Peut-on calculer le nombre de jetons dans lʼurne ?

Non

Oui

Exercice 19 : Loterie.

On considère une roue de loterie à sept secteurs de taille identique et aux couleurs de lʼarc-en-ciel : rouge, orange, jaune, vert, bleu, indigo et violet. On fait tourner la roue et on sʼintéresse à la couleur indiquée.

1

Quelles sont les issues possibles ? Sont-elles équiprobables ?

2

On gagne si lʼaiguille indique le secteur orange. Calculez la probabilité de gagner.

3

Les règles changent : on gagne quand lʼaiguille indique le secteur bleu. La probabilité de gagner a-t-elle changé ?

Oui

Non

4

Les règles changent : on gagne quand lʼaiguille indique le secteur jaune ou le secteur vert. La probabilité de gagner a-t-elle changé ?

Oui

Non

Exercice 20 : On considère une urne qui contient 7 boules rouges, 3 boules vertes et 4 boules bleues.

1

Complétez le tableau suivant.

Exercice 21 : Une urne contient 7 boules vertes, 4 boules rouges, 3 boules bleues et 2 boules jaunes.

On pioche une boule dans lʼurne.

1

Est-on en situation dʼéquiprobabilité ? Justifiez.

2

À quels évènements peut correspondre une probabilité de $\dfrac{7}{16}$ ? Et une probabilité de $\dfrac{1}{4}$ ? Et une probabilité de $\dfrac{5}{16}$ ?

3

Donnez un évènement ayant une probabilité supérieure à $\dfrac{5}{8}$.

Exercice 22 : Une urne contient 3 boules rouges numérotées de 1 à 3 et 4 boules noires numérotées de 4 à 7.

On en tire une au hasard.

1

Les issues sont-elles équiprobables ?

Non

Oui

2

Combien dʼissues réalisent lʼévènement : « Obtenir une boule rouge » ? Quelle est sa probabilité ?

3

Combien dʼissues réalisent lʼévènement : « Obtenir une boule avec un multiple de 3 » ? Quelle est sa probabilité ?

Exercice 23 : Un chapeau de magicien contient 12 foulards indiscernables au toucher : 7 sont verts, 3 sont roses et 2 sont noirs.

1

Quelles sont les issues possibles ? Sont-elles équiprobables ?

2

Calculez la probabilité de tirer : un foulard vert ; un foulard rose ; un foulard noir.