1. Définir une primitive d'une fonction continue f à l'aide d'une équation différentielle y' = f.
2. Calculer une primitive à l'aide des primitives des fonctions de référence et des fonctions de la forme u^{\prime} \times\left(v^{\prime} \circ u\right).
3. Résoudre les équations différentielles de la forme y^{\prime}=a y+b, où a et b sont des réels tels que a \neq 0.
4. Déterminer, à partir d'une solution particulière, toutes les solutions de l'équation différentielle y^{\prime}=a y+f, où a est un réel.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

En 1998, grâce à la datation au carbone 14 (ou datation par comptage du carbone 14 résiduel) sur un fragment de baguette en bois de renne, les peintures ornant les parois de la grotte de Lascaux, située à Montignac, en Dordogne, ont pu être estimées à environ -18 600 ans. Cette technique de datation nécessite de résoudre une équation différentielle. La grotte de Lascaux a été inscrite aux monuments historiques en 1940 et en 1962 et au patrimoine mondial de l'UNESCO en 1979.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Avant de commencer

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Prérequis

1. Connaître les dérivées des fonctions de référence.
2. Connaître la dérivée d'une somme, d'un produit, d'un quotient et d'une fonction de la forme x \mapsto g(a x+b).
3. Connaître les propriétés algébriques de la fonction exponentielle.
4. Connaître la dérivée d'une composée v \circ u.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Anecdote

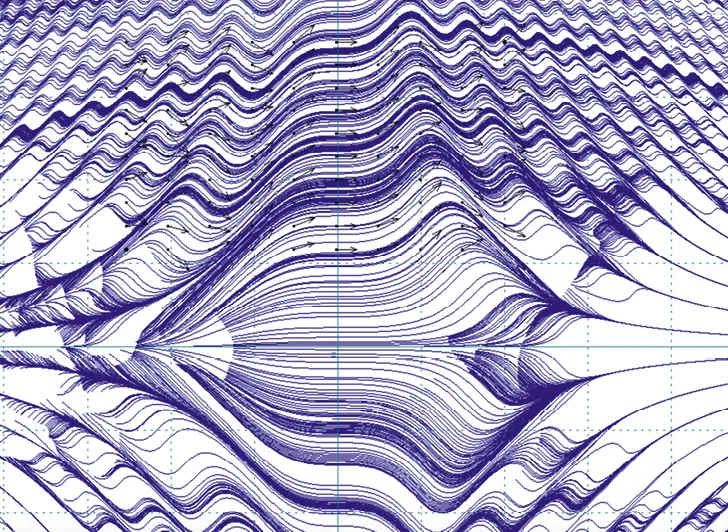
Certaines solutions d'équations différentielles sont difficiles à expliciter mais peuvent être représentées graphiquement. Voici une représentation de certaines solutions de l'équation différentielle y^{\prime}=\sin \left(x^{2} y\right).

Graphique : visualisation d'équations différentielles. Lignes violettes complexes et courbes sur fond blanc.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Dériver des fonctions de référence

Soient f, g, h, k et \ell, des fonctions définies respectivement par f(x)=2 x-3, g(x)=x^{2}, h(x)=\sqrt{x}, k(x)=\frac{1}{x} et \ell(x)=\mathrm{e}^{x}. Pour chacune d'entre elles, déterminer son ensemble de définition, son ensemble de dérivabilité et sa fonction dérivée.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Dériver une somme

Soit f la fonction définie par f(x)=x^{2}+\frac{1}{x}. Déterminer son ensemble de définition, son ensemble de dérivabilité et sa fonction dérivée.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Dériver un produit

Soit g la fonction définie par g(x)=\sqrt{x}(3 x+2). Déterminer son ensemble de définition, son ensemble de dérivabilité et sa fonction dérivée.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

4
Dériver un quotient

Soient h et k les fonctions définies respectivement par h(x)=\frac{1}{x^{3}} et k(x)=\frac{x^{2}+x+1}{x^{2}+1}. Pour chacune d'entre elles, déterminer son ensemble de définition, son ensemble de dérivabilité et sa fonction dérivée.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

5
Dériver une fonction de la forme \boldsymbol{x \mapsto g(a x+b)}.

Soient u et v les fonctions définies respectivement par u(x)=(2-3 x)^{4} et v(x)=\sqrt{1-2 x}. Pour chacune d'entre elles, déterminer son ensemble de définition et, sans étudier son ensemble de dérivabilité, sa fonction dérivée.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

7
Utiliser les propriétés de la fonction exponentielle

Soit f la fonction définie sur \R par f(x)=x \mathrm{e}^{-2 x}. Démontrer que pour tout réel x :

f^{\prime}(x)+2 f(x)=\mathrm{e}^{-2 x}.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

6
Utiliser les propriétés de l'exponentielle

Écrire les expressions suivantes, où x \in \R, sous la forme d'une seule exponentielle. 1. f(x)=\mathrm{e}^{3 x+2} \times \mathrm{e}^{-4 x}

2. g(x)=\frac{\mathrm{e}^{5 x+2}}{\mathrm{e}^{2}}

3. h(x)=\left(\mathrm{e}^{x+1}\right)^{2} \times \mathrm{e}^{-2 x}

4. k(x)=\frac{\mathrm{e}^{3 x+1}}{\mathrm{e}^{2 x-1} \times \mathrm{e}^{2}}

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

8
Dériver une composée

Soient u, v et w les fonctions définies respectivement par u(x)=\sqrt{x^{2}+x+1}, v(x)=\left(x^{2}+x+1\right)^{4} et w(x)=\mathrm{e}^{x^{2}+x+1}. Déterminer l'ensemble de définition de chacune de ces fonctions et, sans étudier leur ensemble de dérivabilité, l'expression de leur fonction dérivée.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

9
Problème

On considère les fonctions f et g définies respectivement sur \R par f(x)=\mathrm{e}^{2 x} et g(x)=-\mathrm{e}^{1-2 x}.
On appelle respectivement \mathcal{C}_f et \mathcal{C}_g leur courbe représentative dans un repère du plan. 1. Justifier que f et g sont dérivables sur \R et déterminer leur fonction dérivée.

2. a. Résoudre dans \R l'équation \mathrm{e}^{2 x}=\mathrm{e}^{1-2 x}.

b. Que peut‑on en déduire pour les courbes \mathcal{C}_f et \mathcal{C}_g ? Justifier.

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Mathématiques Terminale Spécialité

Primitives - Équations différentielles

Avant de commencer

Anecdote

1Dériver des fonctions de référence

2Dériver une somme

3Dériver un produit

4Dériver un quotient

5Dériver une fonction de la forme \boldsymbol{x \mapsto g(a x+b)}.

7Utiliser les propriétés de la fonction exponentielle

6Utiliser les propriétés de l'exponentielle

8Dériver une composée

9Problème

Une erreur sur la page ? Une idée à proposer ?

1
Dériver des fonctions de référence

2
Dériver une somme

3
Dériver un produit

4
Dériver un quotient

5
Dériver une fonction de la forme \boldsymbol{x \mapsto g(a x+b)}.

7
Utiliser les propriétés de la fonction exponentielle

6
Utiliser les propriétés de l'exponentielle

8
Dériver une composée

9
Problème