Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 10
Entraînement 1
Équation différentielle y'=f
14 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58
Flash
L'affirmation suivante est‑elle vraie ou fausse ? Justifier.
« La fonction \text{F} définie par \mathrm{F}(x)=\frac{x^{3}}{3}+\frac{x^{2}}{2}-x+1 est une primitive sur \R de la fonction f définie par f(x)=x^{2}+x+1. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
Flash
Soit f la fonction définie sur \R par f(x)=(x+2) \mathrm{e}^{x}. Étudier le signe de f(x) puis, parmi les trois représentations graphiques proposées, indiquer celle qui correspond à une primitive de f.
Justifier la réponse.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
Flash
Déterminer une équation différentielle de la forme y'=f dont la fonction \text{F} définie sur \R par \mathrm{F}(x)=x \mathrm{e}^{x} est une solution.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans chaque cas, déterminer toutes les primitives de f sur l'intervalle \text{I}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
[Calculer.]
1. f: x \mapsto 2~020 ; \mathrm{I}=\mathbb{R}
2. f: x \mapsto x-1 ; \mathrm{I}=\mathbb{R}
3. f: x \mapsto x^{2}+2 ; \mathrm{I}=\mathbb{R}
4. f: x \mapsto x^{3}-3 x^{2}+3 x-1 ; \mathrm{I}=\mathbb{R}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
[Calculer.]
1. f: x \mapsto x^{4}-x^{3}+x^{2}-x+1 ; \mathrm{I}=\mathbb{R}
2. f: x \mapsto-\frac{1}{3} x^{3}+\frac{1}{2} x^{2}-x+2 ; \mathrm{I}=\mathbb{R}
3. f: x \mapsto \frac{2}{3} x^{3}-\frac{3}{4} x^{2}+\frac{4}{5} x-\frac{5}{6} ; \mathrm{I}=\mathbb{R}
4. f: x \mapsto x^{3}-\frac{1}{2} x^{2}+\frac{1}{3} x-\frac{1}{4} ; \mathrm{I}=\mathbb{R}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
[Calculer.]
1. f: x \mapsto-\frac{3}{\sqrt{x}} ; \mathrm{I}=]0~;+\infty[
2. f: x \mapsto \frac{2}{x^{2}} ; \mathrm{I}=]-\infty~; 0[
2. f: x \mapsto \frac{2}{x^{2}} ; \mathrm{I}=]-\infty~; 0[
3. f: x \mapsto x^{2}+x-\frac{1}{x^{2}} ; \mathrm{I}=]-\infty~; 0[
4. f: x \mapsto \frac{3 x-2}{x^{3}} ; \mathrm{I}=]0~;+\infty[
4. f: x \mapsto \frac{3 x-2}{x^{3}} ; \mathrm{I}=]0~;+\infty[
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
[Calculer.]
1. f: x \mapsto-\frac{1}{(x+2)^{2}} ; \mathrm{I}=]-\infty~;-2[
2. f: x \mapsto \frac{2}{(x+3)^{2}} ; \mathrm{I}=]-3~;+\infty[
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
[Calculer.]
1. f: x \mapsto \frac{x}{\left(x^{2}+2\right)^{3}} ; \mathrm{I}=\mathbb{R}
2. f: x \mapsto \frac{3 x^{2}}{\left(x^{3}-1\right)^{4}} ; \mathrm{I}=]1~;+\infty[
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
66
[Calculer.]
1. f: x \mapsto 2 \mathrm{e}^{2 x} ; \mathrm{I}=\mathbb{R}
2. f: x \mapsto \mathrm{e}^{1-3 x} ; \mathrm{I}=\mathbb{R}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
67
[Calculer.]
1. f: x \mapsto-x \mathrm{e}^{x^{2}-1} ; \mathrm{I}=\mathbb{R}
2. f: x \mapsto \frac{\mathrm{e}^{x}}{\left(\mathrm{e}^{x}+1\right)^{2}} ; \mathrm{I}=\mathbb{R}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
68
[Calculer.]
1. f: x \mapsto \frac{x}{\sqrt{x^{2}+1}} ; \mathrm{I}=\mathbb{R}
2. f: x \mapsto-\frac{3 x^{2}}{\sqrt{x^{3}+1}} ; \mathrm{I}=]-1~;+\infty[
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
69
[Communiquer.]
Un logiciel de calcul formel donne le résultat suivant lorsqu'on lui demande de déterminer une primitive de x \mapsto 3 \mathrm{e}^{2 x}.
Le zoom est accessible dans la version Premium.
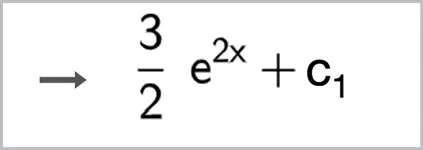
Expliquer la réponse obtenue.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
70
[Communiquer.]
Guillaume a demandé à un logiciel de calcul formel de déterminer la dérivée d'une fonction. Il obtient le résultat suivant.
Le zoom est accessible dans la version Premium.
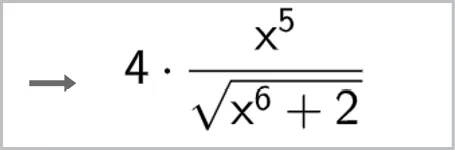
Déterminer une fonction qui aurait pu être utilisée par Guillaume.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Déterminer la solution sur \text{I} de l'équation différentielle donnée qui prend la valeur y_0 en x_0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
71
[Calculer.]
1. y^{\prime}=x^{3}-2 x ; \mathrm{I}=\mathbb{R} ; x_{0}=0 ; y_{0}=2
2. y^{\prime}=-\frac{2}{x^{2}}+x-1 ; \mathrm{I}=]0~;+\infty[ ; x_{0}=1 ; y_{0}=\frac{1}{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
72
[Calculer.]
1. y^{\prime}=-x^{3}+x^{2}-x+1 ; \mathrm{I}=\mathbb{R} ; x_{0}=1 ; y_{0}=\frac{1}{12}
2. y^{\prime}=-\frac{1}{x^{3}}+\frac{1}{x^{2}}-x+\frac{1}{2} ; \mathrm{I}=]-\infty~; 0[ ; x_{0}=-1 ; y_{0}=-\frac{1}{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
73
[Calculer.]
1. y^{\prime}=1-\frac{1}{2 \sqrt{x}} ; \mathrm{I}=]0~;+\infty[ ; x_{0}=2 ; y_{0}=-\sqrt{2}
2. y^{\prime}=3 \mathrm{e}^{x} ; \mathrm{I}=\R ; x_{0}=1 ; y_{0}=\mathrm{e}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
74
[Calculer.]
1. y^{\prime}=\mathrm{e}^{2 x}+2 \mathrm{e}^{-\normalsize{\tfrac{x}{2}}} ; \mathrm{I}=\mathbb{R} ; x_{0}=0 ; y_{0}=\frac{1}{2}
2. y^{\prime}=2 x\left(x^{2}+1\right)^{3} ; \mathrm{I}=\R ; x_{0}=-0 ; y_{0}=-\frac{3}{4}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
75
[Calculer.]
1. y^{\prime}=\frac{\mathrm{e}^{2 x}}{\left(\mathrm{e}^{2 x}+1\right)^{3}} ; \mathrm{I}=\R ; x_{0}=0 ; y_{0}=-\frac{1}{16}
2. y^{\prime}=\frac{2 x}{\sqrt{2 x^{2}+1}} ; \mathrm{I}=\R ; x_{0}=2 ; y_{0}=2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
76
[Représenter.]
Parmi les fonctions g et h représentées ci‑dessous, quelle est celle qui correspond à une primitive de la fonction f ?
Le zoom est accessible dans la version Premium.
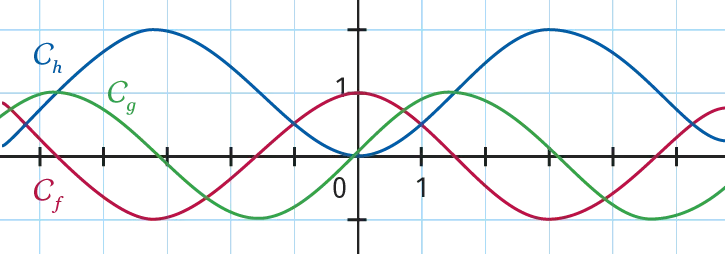
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
77
[Représenter.]
On a représenté deux fonctions f et g définies sur \R dans un repère du plan. Déterminer laquelle des deux est une primitive de l'autre.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
78
[Représenter.]
On donne la représentation graphique d'une fonction f définie sur l'intervalle \mathrm{I}=[-3~; 2] dans un repère du plan. Déterminer, en justifiant, les variations d'une primitive \text{F} de f sur \text{I}.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
79
Vrai / Faux
[Raisonner.]
f et \text{F} sont deux fonctions définies sur un intervalle \text{I} de \R et k est un réel.
Pour chacune des propositions suivantes, indiquer si elle est vraie ou fausse en justifiant.
1. Si\text{ F} est positive et dérivable sur \text{I} avec \mathrm{F}'=f, alors f est croissante sur \text{I}.
2. Si \text{F} est décroissante et dérivable sur \text{I} avec \mathrm{F}^{\prime}=f, alors f est négative sur \text{I}.
3. Si \mathrm{F}^{\prime}=f, alors f est une primitive de \text{F} sur \text{I}.
2. Si \text{F} est décroissante et dérivable sur \text{I} avec \mathrm{F}^{\prime}=f, alors f est négative sur \text{I}.
3. Si \mathrm{F}^{\prime}=f, alors f est une primitive de \text{F} sur \text{I}.
4. Si \mathrm{F}^{\prime}=f, alors \text{F} est une primitive de f sur \text{I}.
5. Si \text{F} est une primitive de f sur \text{I}, alors \mathrm{F} + k est une primitive de f sur \text{I}.
5. Si \text{F} est une primitive de f sur \text{I}, alors \mathrm{F} + k est une primitive de f sur \text{I}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
80
[Calculer.]
Soit f la fonction définie sur \mathrm{I}=]0~; 1[ par :
f(x)=\frac{2 x-1}{x^{2}(x-1)^{2}}.
1. Déterminer les réels a et b tels que, pour tout x \in \mathrm{I} :
f(x)=\frac{a}{x^{2}}+\frac{b}{(x-1)^{2}}.
2. En déduire les solutions de l'équation différentielle y'=f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
81
[Calculer.]
Soit f la fonction définie sur \mathrm{I}=]1~;+\infty[ par :
f(x)=\frac{x^{2}-2 x}{(x-1)^{2}}.
1. Déterminer les réels a et b tels que, pour tout x \in \mathrm{I} :
f(x)=a+\frac{b}{(x-1)^{2}}.
2. En déduire les solutions de l'équation différentielle y'=f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
82
[Calculer.]
Soit f la fonction définie sur \mathrm{I}=]-2~;+\infty[ par :
f(x)=\frac{2 x^{3}+9 x^{2}+12 x+2}{(x+2)^{2}}.
1. Déterminer les réels a, b et c tels que, pour tout x \in \mathrm{I} :
f(x)=a x+b+\frac{c}{(x+2)^{2}}.
2. En déduire les solutions de l'équation différentielle y'=f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
83
[Calculer.]
Soit f la fonction définie sur \mathrm{I}=]-2~;2[ par :
f(x)=\frac{x}{\left(x^{2}-4\right)^{2}}.
1. Factoriser l'expression \left(x^{2}-4\right)^{2}.2. Déterminer les réels a et b tels que, pour tout x \in \mathrm{I} :
f(x)=\frac{a}{(x-2)^{2}}+\frac{b}{(x+2)^{2}}.
3. En déduire les solutions de l'équation différentielle y'=f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
84
[Calculer.]
Soit f la fonction définie sur \mathrm{I}=]-1~;1[ par :
f(x)=\frac{x\left(x^{2}+3\right)}{\left(x^{2}-1\right)^{3}}.
1. Factoriser l'expression \left(x^{2}-1\right)^{3}.2. Déterminer les réels a et b tels que, pour tout x \in \mathrm{I} :
f(x)=\frac{a}{(x-1)^{3}}+\frac{b}{(x+1)^{3}}.
3. En déduire les solutions de l'équation différentielle y'=f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
85
[Calculer.]
Soit f la fonction définie sur \mathrm{I}=]-1~;1[ par :
f(x)=\frac{x^{2}+1}{\left(x^{2}-1\right)^{2}}.
1. Démontrer que, pour tout x \in \mathrm{I}, x^{2}+1=\frac{1}{2}\left((x+1)^{2}+(x-1)^{2}\right).2. En déduire les solutions de l'équation différentielle y'=f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
86
[Représenter.]
Dans chaque cas, représenter dans un repère orthogonal la solution \text{F} de l'équation différentielle telle que \mathrm{F}\left(x_{0}\right)=y_{0}. 1. y^{\prime}=|x| ; x_{0}=y_{0}=0
GeoGebra
2. y^{\prime}=|x|+|x-1| ; x_{0}=\frac{1}{2} ; y_{0}=1
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
87
[Calculer.]
Résoudre les équations différentielles après les avoir transformées, en précisant l'ensemble de définition des solutions.
1. x^{2} y^{\prime}=-1
2. \sqrt{x} y^{\prime}+1=0
2. \sqrt{x} y^{\prime}+1=0
3. x^{4} y^{\prime}=3(x-1)^{2}
4. \mathrm{e}^{2 x} y^{\prime}=-\mathrm{e}^{x}
4. \mathrm{e}^{2 x} y^{\prime}=-\mathrm{e}^{x}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
88
[Calculer.]
Soit y une fonction dérivable sur un intervalle \text{I} telle que y' est également dérivable sur \text{I}. On note y'' la dérivée de y'. On souhaite résoudre l'équation différentielle (\mathrm{E}): y^{\prime \prime}=-4 x+3. 1. On pose z = y'. Déterminer une équation différentielle (\mathrm{E'}), d'inconnue z, équivalente à (\mathrm{E}).
2. Résoudre cette équation différentielle.
3. À partir des solutions z de (\mathrm{E'}), déterminer toutes les solutions y de (\mathrm{E}).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
89
[Calculer.]
Résoudre les équations différentielles après les avoir transformées, en précisant l'ensemble de définition des solutions. On rappelle que si y et y' sont dérivables sur un intervalle \text{I}, on peut définir sur \text{I} la fonction dérivée de y' que l'on note y''.
Aide
Poser z = y'.
2. y^{\prime \prime}=\mathrm{e}^{x}+\mathrm{e}^{-x}
3. x^{3} y^{\prime \prime}=-2
4. \mathrm{e}^{2 x} y^{\prime \prime}=4
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
90
[Calculer.]
1. Montrer que l'équation différentielle y^{\prime}=\frac{x^{3}+x^{2}+x+1}{\sqrt{x-1}} admet sur \mathrm{I}=]1~;+\infty[ une solution de la forme x \mapsto\left(a x^{3}+b x^{2}+c x+d\right) \sqrt{x-1} où a, b, c et d sont des réels que l'on déterminera.
2. En déduire les solutions sur \text{I} de cette équation.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah