L'usine de biomasse de Perpignan permet de récupérer chaque année environ 29,5 tonnes de méthane à partir de 90 tonnes de déchets organiques. Après combustion, l'énergie chimique du méthane est transformée en électricité.

Une valorisation possible du dioxyde de carbone \text{CO}_{2} consiste à le capter en sortie d'usine pour le stocker et l'utiliser pour fabriquer des boissons gazeuses notamment.

1. Représenter la chaîne énergétique d'une telle centrale.

Cliquez pour accéder à une zone de dessin

2. Écrire l'équation de combustion complète du méthane.

3. Calculer la masse de dioxyde de carbone \text{CO}_{2} produite chaque année par cette centrale.

4. Combien de bouteilles d'un litre peut-on gazéifier après captage du \text{CO}_{2} en sortie de cette centrale ?

Données

M(\mathrm{CH}_{4})=16\text{,}0 g·mol^-1 ;
Concentration en \bf{\text{CO}_{2}} par litre de soda : 7 g·L^‑1.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

22
Le briquet à gaz

✔ RAI/MOD : Appliquer le principe de conservation de l'énergie

Le briquet à gaz est une invention du français Henry Pingeot. Environ 9,0 mL de butane (\mathrm{C}_{4} \mathrm{H}_{10}) sont stockés dans le briquet à l'état liquide et ce butane s'échappe du briquet à l'état gazeux avant de subir une combustion.

1. Nommer le changement d'état physique qui a lieu avant la combustion.

2. Calculer la quantité de matière de butane contenue dans le briquet.

3. Écrire l'équation de combustion complète du butane.

4. Calculer l'énergie maximale que peut libérer un briquet.

Données

M(\mathrm{C}_{4} \mathrm{H}_{10})=58\text{,}1 g·mol^-1 ;
\rho(\mathrm{C}_{4} \mathrm{H}_{10})=0\text{,}573 kg·L^-1 ;
E_{\mathrm{f}}=11\,000 kJ·mol^-1 ;
E_{\mathrm{d}}=8\,122 kJ·mol^-1.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

23
Comprendre les attendus
Jeux olympiques

✔ RAI/MOD : Transformation chimique

La flamme olympique est un symbole des jeux, elle reste allumée tout au long de l'année et sa température est de l'ordre de 1 000 °C. Elle est alimentée par du propane qui arrive par un tuyau dans le manche de la torche qui alimente en continu la combustion de ce gaz.

1. Écrire l'équation de combustion complète du propane \mathrm{C}_{3} \mathrm{H}_{8}.

2. Déterminer le volume de \mathrm{CO}_{2} produit pour 1 kg de propane consommé.

3. La flamme olympique participe-t-elle au réchauffement climatique ?

4. Rappeler ce qu'est l'effet de serre.

Données

M(\mathrm{C}_{3} \mathrm{H}_{8})=44\text{,}1 g·mol^-1 ;
\rho(\mathrm{C0}_{2})=1\text{,}87 g·L^-1 ;

Détails du barème
TOTAL /5,5 pts

0,5 pt

1 pt

1 pt + 0,5 pt

\mathrm{CO}_{2}

1 pt

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

24
Mieux isoler pour économiser de l'énergie

✔ APP : Extraire l'information utile

Près de 29 % des Français se chauffent au fioul, un combustible composé essentiellement d'alcanes de formule brute \mathrm{C}_{16} \mathrm{H}_{34}. La consommation annuelle d'énergie par m² pour se chauffer est de 250 kWh. Cette quantité d'énergie représente une réelle part du budget des Français. Pour diminuer la consommation en carburant, une solution est d'améliorer l'isolation des maisons.

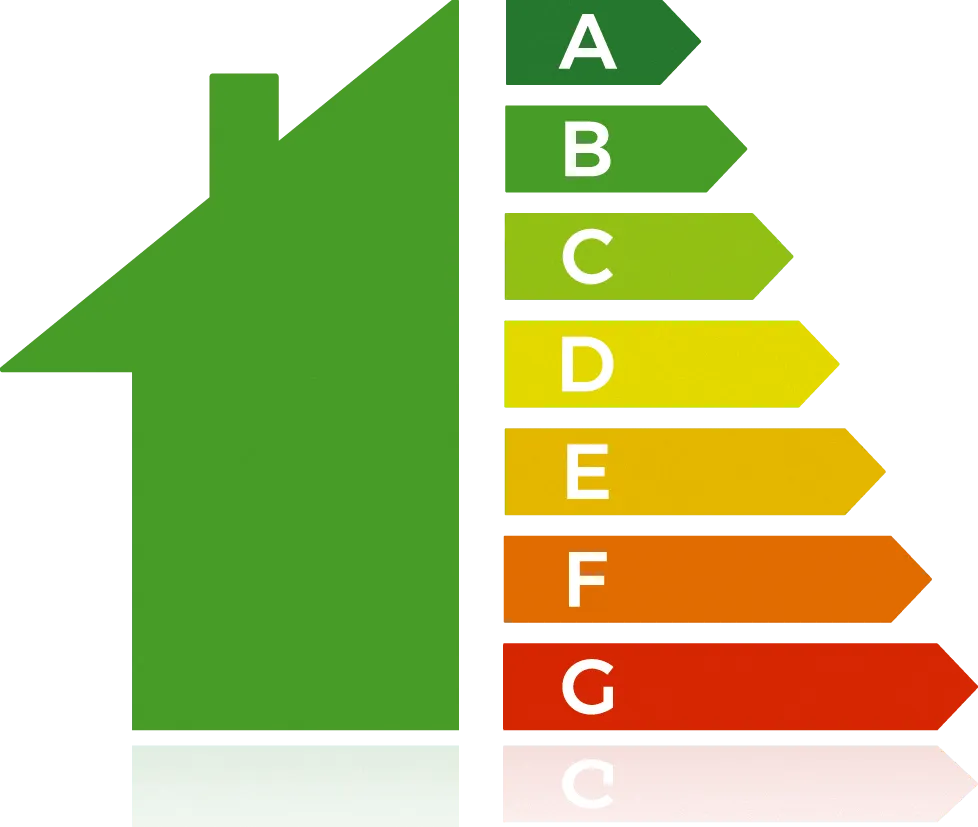
A : le logement consomme moins de 50 kW·h·m^‑2·an^‑1.
B : le logement consomme entre 51 et 90 kW·h·m^‑2·an^‑1.
C : le logement consomme entre 91 et 150 kW·h·m^‑2·an^‑1.
D : le logement consomme entre 151 et 230 kW·h·m^‑2·an^‑1.
E : le logement consomme entre 231 et 330 kW·h·m^‑2·an^‑1.
F : le logement consomme entre 331 et 450 kW·h·m²·an^‑1.
G : le logement consomme plus de 450 kW·h·m^‑2·an^‑1.

1. Déterminer l'énergie minimale A et maximale G consommée pour un logement de 50 m² en une année.

2. Écrire l'équation de combustion complète du fioul.

3. Déterminer l'énergie molaire de réaction du fioul.

4. Calculer la consommation par année de litres de fioul pour un logement de 50 m² type A et G.

5. L'isolation de l'habitat est-elle une vraie solution économique ?

6. Déterminer le volume de \text{CO}_{2} émis par ces deux logements de 50 m² type A et G.

7. Quel autre atout comporte l'isolation de l'habitat ?

Données

Un alcane possède \text{C}_{n} \text{H}_{2 n+2} possède n - 1 liaisons \text{C} - \text{C} et 2n + 2 liaisons \text{C} - \text{H} ;
1 kWh = 3\text{,}6 MJ ;
M(C_{16} \mathrm{H}_{34})=226\text{,}4 g·mol^-1 ;
M(\mathrm{CO}_{2})=44\text{,}0 g·mol^-1 ;
\rho(\mathrm{CO}_{2})=1\text{,}87g·L^-1 ;
\rho(\text{C}_{16} \text{H}_{34})=0\text{,}773 kg·L^-1 ;
E_{\text{l}}(\text{C}-\text{C})=346 kJ·mol^-1 ;
E_{\text{l}}(\text{C}-\text{H})=411 kJ·mol^-1 ;
E_{\text{l}}(\text{O}-\text{H})=459 kJ·mol^-1 ;
E_{\text{l}}(\text{C}=\text{O})=795 kJ·mol^-1 ;
E_{\text{l}}(\text{O}=\text{O})=494 kJ·mol^-1 ;
V_{\mathrm{m}}(\mathrm{CO}_{2})=23\text{,}5 L·mol^-1.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

25
La banane flambée

✔ RAI/MOD : Appliquer le principe de conservation de l'énergie

La banane flambée est un dessert dans lequel une combustion complète de l'éthanol a lieu.

1. Calculer la quantité de matière d'éthanol nécessaire à la recette de la banane flambée.

2. Calculer l'énergie molaire de réaction de combustion complète de l'éthanol.

3. En déduire l'énergie libérée par combustion lors de cette recette.

Doc. 1
Recette des bananes flambées

Ingrédients pour 5 personnes :

5 bananes ;
15 g de beurre ;
15 cL de rhum ;
Un peu de jus de citron ;
4 cuillerées à soupe de sucre roux ;
3 gouttes d'extrait de vanille.

Doc. 2
Le rhum

Le rhum est une boisson alcoolisée fabriquée à partir de la canne à sucre. Il contient de l'éthanol, sa concentration en éthanol est de 40 % vol.
% vol : rapport entre le volume d'alcool (éthanol) contenu dans le mélange et le volume total de ce mélange.

Données

M(\text{C}_{2} \text{H}_{6} \text{O})=46 g·mol^-1 ;
\rho(\mathrm{C}_{2} \mathrm{H}_{6} \mathrm{O})=0\text{,}789 kg·L^-1 ;
E_{\text{l}}(\text{C}-\text{C})=346 kJ·mol^-1 ;
E_{\text{l}}(\text{C}-\text{H})=411 kJ·mol^-1 ;
E_{\text{l}}(\text{O}-\text{H})=459 kJ·mol^-1 ;
E_{\text{l}}(\text{C}=\text{O})=795 kJ·mol^-1 ;
E_{\text{l}}(\text{C}-\text{O})=358 kJ·mol^-1 ;
E_{\text{l}}(\text{O}=\text{O})=494 kJ·mol^-1.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

26
Copie d'élève à commenter

Proposer une justification pour chaque erreur relevée par le correcteur.

1. L'équation de combustion complète du pentan-1-ol (\text{C}_{5} \text{H}_{12} \text{O}) est :
\xcancel{\color{red}\color{black}\{\text{C}_{5}\text{H}_{12}\text{O}(\text{l}) + 5\, \text{O}_{2}(\text{g}) \rightarrow 5\, \text{CO}(\text{g}) + 6 \,\text{H}_{2}\text{O}(\text{g})}.

2. L'équation de combustion complète du pentan-1-ol participe à l'effet de serre car ~~il consomme du dioxygène.~~

3. L'énergie ~~massique~~
de dissociation de cette réaction est égale à :
\xcancel{\color{red}\color{black}\{E_{\text{d}}=4 El(\text{C}-\text{C})+12 E_{\text{l}}(\text{H}-\text{C})+E_{\text{l}}(\text{O}-\text{C})+\dfrac{15}{2} E_{\text{l}}(\text{O}=\text{O})}
= 10\, 522 kJ·mol^-1.

4. L'énergie molaire de ~~réaction~~
est égale à :
E_{\text{f}}=5 E_{\text{l}}(\text{C}=\text{O})+6 E_{\text{l}}(\text{O}-\text{H})=13\,518 kJ·mol^-1.

5. L'énergie molaire de réaction est égale à :
E_{\text{r}}=2\,996 ~~kJ·kg^-1.~~

6. Cette réaction est dite ~~endothermique~~.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

27
Butane ou propane, lequel choisir ?

✔ VAL : Réaliser une analyse comparative

Environ 53 millions de bouteilles de gaz sont vendues chaque année en France auprès de 10 millions de clients. Le choix se fait essentiellement entre du propane et du butane. Comment savoir quel combustible choisir ?

1. Écrire les équations de combustions complètes de chaque gaz.

2. En vous aidant de la table d'énergies des liaisons

p. 195

, estimer l'énergie molaire de réaction pour la combustion de chacun de ces gaz.

3. Les bouteilles de gaz usuelles contenant 13 kg de combustible, déterminer l'énergie libérée par combustion pour chaque bouteille.

4. D'après les résultats, quelle bouteille de gaz faut-il privilégier ? Justifier par une phrase.

5. Faire une recherche internet pour expliquer pourquoi deux types de combustibles existent dans le commerce.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

28
TNT, une combustion explosive

✔ RAI/ANA : Faire le lien entre les modèles microscopiques et les grandeurs macroscopiques

Le TNT ou 2,4,6-trinitrotoluène est un explosif découvert par le chimiste allemand Julius Wilbrand. Le TNT fut très utilisé lors de la Première Guerre mondiale, notamment pour la confection de torpilles. Selon les conditions opératoires, deux réactions différentes peuvent se produire à partir du TNT :
a. 2\, \mathrm{C}_{7} \mathrm{H}_{5} \mathrm{N}_{3} \mathrm{O}_{6}(\mathrm{s})+\mathrm{O}_{2}(\mathrm{g}) \rightarrow 3\, \mathrm{N}_{2}(\mathrm{g})+5\, \mathrm{H}_{2}(\mathrm{g})+14\, \mathrm{CO}(\mathrm{g}).
b. \mathrm{C}_{7} \mathrm{H}_{5} \mathrm{N}_{3} \mathrm{O}_{6}(\mathrm{s})+4\, \mathrm{O}_{2}(\mathrm{g}) \rightarrow 7\, \mathrm{CO}_{2}(\mathrm{g})+\mathrm{H}_{2} \mathrm{O}(\mathrm{g})+\mathrm{N}_{2}(\mathrm{g}).

1. Nommer chacune de ces réactions.

2. La réaction b. ne se produit pratiquement pas, proposer une explication.

3. En s'aidant des données, déterminer l'énergie libérée lors de la combustion de 2 kg de TNT et de 2 kg de sucre lors de leur combustion.

4. Le résultat précédent est-il cohérent ? Proposer une explication.

Données

M_{\mathrm{TNT}}=227\text{,}1 g·mol^-1 ;
M_{\text {sucre}}=342\text{,}3 g·mol^-1 ;
E_{\mathrm{r}}(\mathrm{TNT})=3\text{,}29 MJ·mol^-1 ;
E_{\mathrm{r}}(\text {sucre})=5\text{,}72 MJ·mol^-1.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

29
Efforts musculaires

✔ RÉA : Exploiter un ensemble de mesures

Martin Fourcade est quintuple champion olympique de biathlon et a été 11 fois champion du monde.

Ce sport nécessite à la fois endurance sur les skis et concentration lors des tirs de précision. Face à son grand rival, le Norvégien Johannes Bø, Martin Fourcade (77 kg) gagne ses victoires au mental. Comment vérifier cette affirmation ?

1. Écrire les équations ajustées des processus aérobie (doc. 2) et anaérobie (doc. 3).

2. Lors d'une course d'une heure, quelle est la quantité de matière maximale de \text{O}_{2} consommée par chaque biathlète ?

3. En considérant le dioxygène comme le réactif limitant de la réaction aérobie, quel athlète atteint le processus d'anaérobie le premier pour une même énergie dépensée par unité de temps ?

4. D'après vos résultats, justifier l'affirmation faite dans l'énoncé.

Doc. 1
\text{V}\text{O}_{2} max

Le Volume d'oxygène maximum (\text{V}\text{O}_{2} max) est la quantité maximale d'oxygène que le corps consomme lors d'un effort intense par unité de temps. Il s'exprime en millilitres par minute (mL·min^‑1).

Doc. 2
Aérobie

L'aérobie est un processus musculaire de combustion complète du glucose \mathrm{C}_{6} \mathrm{H}_{12} \mathrm{O}_{6} contenu dans l'organisme.

Doc. 3
Anaérobie

Lorsque la quantité de dioxygène n'est plus suffisante, le glucose \mathrm{C}_{6} \mathrm{H}_{12} \mathrm{O}_{6} se transforme en acide lactique \mathrm{C}_{3} \mathrm{H}_{6} \mathrm{O}_{3}, qui peut déclencher des crampes.

Données

M(\text{O}_{2})=32\text{,}0 g·mol^-1 ;
\mathrm{VO}_{2} \text { max (Martin Fourcade) } = 82 mL·kg ^-1·min^-1 ;
\mathrm{VO}_{2} \text{ max }(\text {Johannes}\: \mathrm{B} \phi)=87 mL·kg^-1·min^-1;
Volume molaire d'un gaz dans les CNTP :
V_{\text{m}}=22\text{,}4 L·mol^-1.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Détermination d'une énergie de combustion

✔ RAI/MOD : Appliquer le principe de conservation de l'énergie

L'éthanol (\text{C}_2\text{H}_6\text{O}) est le composant principal de l'alcool à brûler (plus de 90 %). On cherche à déterminer son énergie de combustion. Pour cela, on place dans un calorimètre un récipient contenant un volume d'eau : \text{V}_{\text{eau}} = 400 \text{mL} au‑dessus d'un brûleur contenant une masse \text{m} = 5,0 \text{g} d'éthanol (voir schéma). On plonge un thermomètre dans l'eau puis on allume le brûleur. Le dioxygène est en excès, et on constate que lorsque tout l'éthanol a brûlé, la température, initialement de 20°C, est passée à 88°C. On suppose que toute l'énergie dégagée par la combustion est transmise à l'eau (cas d'un calorimètre idéal).

Données

Énergie nécessaire pour augmenter la température de l'eau (par unité de masse et par °C de hausse de la température) : \text{c}_{\text{H}_{2}\text{O}} = 4,18 J·g^{-1}·°C^{-1}.

1. Calculer l'énergie \text{E}_{\text{th}} reçue par l'eau.

2. Écrire et ajuster la réaction de combustion de l'éthanol.

3. Calculer la quantité de matière \text{n}_{\text{ol}} d'éthanol ayant brûlé.

4. En déduire l'énergie molaire de cette réaction \text{E}_{\text{comb}}(éthanol).

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Physique-Chimie 1re Spécialité

Pour s'entraîner

20Valorisation du \bf{\text{CO}_{2}}

21 Des énergies variées en QCM

22Le briquet à gaz

23Comprendre les attendusJeux olympiques

Détails du barème TOTAL /5,5 pts

24Mieux isoler pour économiser de l'énergie

25La banane flambée

26Copie d'élève à commenter

27Butane ou propane, lequel choisir ?

28 TNT, une combustion explosive

29Efforts musculaires

ADétermination d'une énergie de combustion

Une erreur sur la page ? Une idée à proposer ?

20
Valorisation du \bf{\text{CO}_{2}}

21

Des énergies variées en QCM

22
Le briquet à gaz

23
Comprendre les attendus
Jeux olympiques

Détails du barème
TOTAL /5,5 pts

24
Mieux isoler pour économiser de l'énergie

25
La banane flambée

26
Copie d'élève à commenter

27
Butane ou propane, lequel choisir ?

28
TNT, une combustion explosive

29
Efforts musculaires

A
Détermination d'une énergie de combustion