Physique-Chimie Terminale Spécialité
Mes Pages
Préparation aux épreuves du Bac
1. Constitution et transformations de la matière
Ch. 1
Modélisation des transformations acide-base
Ch. 2
Analyse physique d'un système chimique
Ch. 3
Méthode de suivi d'un titrage
Ch. 4
Évolution temporelle d'une transformation chimique
Ch. 5
Évolution temporelle d'une transformation nucléaire
BAC
Thème 1
Ch. 6
Évolution spontanée d'un système chimique
Ch. 7
Équilibres acide-base
Ch. 8
Transformations chimiques forcées
Ch. 9
Structure et optimisation en chimie organique
Ch. 10
Stratégies de synthèse
BAC
Thème 1 bis
2. Mouvement et interactions
Ch. 11
Description d'un mouvement
Ch. 12
Mouvement dans un champ uniforme
Ch. 13
Mouvement dans un champ de gravitation
Ch. 14
Modélisation de l'écoulement d'un fluide
BAC
Thème 2
3. Conversions et transferts d'énergie
Ch. 15
Étude d’un système thermodynamique
Ch. 16
Bilans d'énergie thermique
BAC
Thème 3
4. Ondes et signaux
Ch. 17
Propagation des ondes
Ch. 18
Interférences et diffraction
Ch. 19
Lunette astronomique
Ch. 20
Effet photoélectrique et enjeux énergétiques
Ch. 21
Évolutions temporelles dans un circuit capacitif
BAC
Thème 4
Annexes
Ch. 22
Méthode
Chapitre 5
Exercices
Pour s'échauffer - Pour commencer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
| Pour s'échauffer | Pour commencer | Différenciation | Pour s'entraîner | |
|---|---|---|---|---|
| Savoir identifier un type de désintégration radioactive | | |||
| Savoir écrire et équilibrer l'équation d'une réaction radioactive | ||||
| Savoir exploiter la loi et la courbe de décroissance radioactive |
Retrouvez bientôt les exercices du parcours d'apprentissage autocorrigés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour s'échauffer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Désintégration
On considère l'équation de réaction suivante :
_{\;59}^{145}\text{Pr} \rightarrow \ _{\;60}^{145}\text{Nd} + \ _{-1}^{\enspace 0}\text{e}^-
Identifier le type de radioactivité et la particule émise.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Désintégration
On considère l'équation de réaction suivante :
_Z^A\text{X} \rightarrow \ ^{148}_{\;62}\text{Sm} + \ _2^4\text{He}
1. Identifier le type de radioactivité.
2. Déterminer la composition du noyau radioactif avant sa désintégration et à quel élément il correspond.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7Lois de conservation
Énoncer les lois de conservation lors d'une désintégration radioactive.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8Activité radioactive
Un échantillon de roche contenant du cobalt 59, bombardé artificiellement par des neutrons, contient dès lors 57 \times 10^{17} noyaux de cobalt 60. Au bout de 2 min, il n'en reste plus que 23 \times 10^{16}.Déterminer l'activité radioactive de cette roche.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9Constante radioactive
Le titane 53 est un noyau radioactif qui se désintègre en émettant un électron. Il possède un temps de demi-vie t_{1/2} = 32{,}7 s.1. Écrire l'équation de désintégration du titane 53.
2. Calculer la constante radioactive \lambda du titane 53.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10Décroissance radioactive
1. Écrire la loi de décroissance radioactive.2. Définir chaque grandeur et les unités associées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AChaîne de désintégrations
Compléter la chaîne de désintégration du radium 226.
_{88}^{226}\text{Ra} \rightarrow _{\cdots}^{\cdots}\text{Rn} (émission \alpha)
_{\cdots}^{\cdots}\text{Rn} \rightarrow _{\cdots}^{\cdots}\text{Po} (émission \alpha)
_{\cdots}^{\cdots}\text{Po} \rightarrow _{82}^{\cdots}\text{Pb} (émission \dots)
_{82}^{\cdots}\text{Pb} \rightarrow _{\cdots}^{\cdots}\text{Bi} (émission \beta^-)
_{\cdots}^{\cdots}\text{Bi} \rightarrow _{84}^{214} \dots (émission \dots)
_{84}^{214} \cdots \rightarrow _{82}^{\cdots}\text{Pb} (émission \dots)
_{82}^{\cdots}\text{Pb} \rightarrow _{\cdots}^{210} \dots (émission \beta^-)
_{\cdots}^{210} \cdots \rightarrow _{84}^{\cdots}\text{Po} (émission \beta^-)
_{84}^{\cdots}\text{Po} \rightarrow _{82}^{206}\text{Pb} (émission \dots)
_{88}^{226}\text{Ra} \rightarrow _{\cdots}^{\cdots}\text{Rn} (émission \alpha)
_{\cdots}^{\cdots}\text{Rn} \rightarrow _{\cdots}^{\cdots}\text{Po} (émission \alpha)
_{\cdots}^{\cdots}\text{Po} \rightarrow _{82}^{\cdots}\text{Pb} (émission \dots)
_{82}^{\cdots}\text{Pb} \rightarrow _{\cdots}^{\cdots}\text{Bi} (émission \beta^-)
_{\cdots}^{\cdots}\text{Bi} \rightarrow _{84}^{214} \dots (émission \dots)
_{84}^{214} \cdots \rightarrow _{82}^{\cdots}\text{Pb} (émission \dots)
_{82}^{\cdots}\text{Pb} \rightarrow _{\cdots}^{210} \dots (émission \beta^-)
_{\cdots}^{210} \cdots \rightarrow _{84}^{\cdots}\text{Po} (émission \beta^-)
_{84}^{\cdots}\text{Po} \rightarrow _{82}^{206}\text{Pb} (émission \dots)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour commencer
Équation de réaction nucléaire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11Types de radioactivités
✔ APP : Maîtriser le vocabulaire du cours
Voici une chaîne de désintégration à partir du thorium 232.
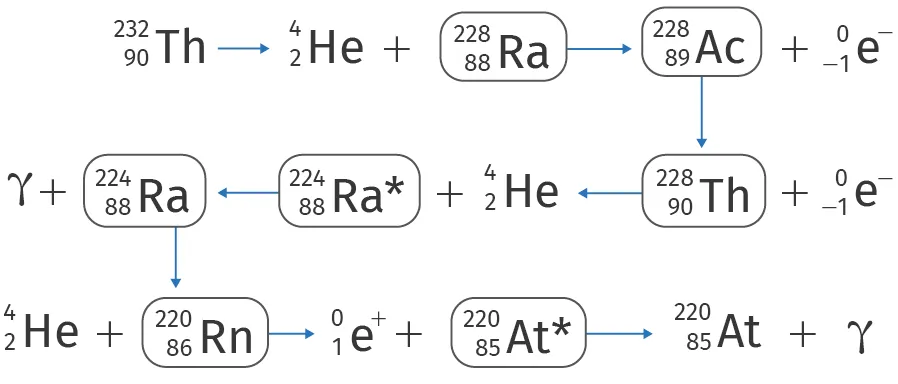
Identifier à chaque étape le type de radioactivité.
Identifier à chaque étape le type de radioactivité.
Compteur Geiger sensible aux rayonnements \alpha, \beta et \gamma.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12Équation radioactive
✔ RAI/MOD : Modéliser une transformation
1. Compléter les équations suivantes en précisant la particule p et le noyau fils _Z^A\text{X}.
a. (\beta ^+) _{\;8}^{15}\text{O} \rightarrow \ _Z^A\text{X} + \text{p}
b. (\beta ^-) _1^3\text{H} \rightarrow \ _Z^A\text{X} + \text{p}
c. (\gamma) _{\;91}^{234}\text{Pa}^* \rightarrow \ _Z^A\text{X} + \text{p}
d. (\alpha) _{\;84}^{212}\text{Po} \rightarrow \ _Z^A\text{X} + \text{p}
a. (\beta ^+) _{\;8}^{15}\text{O} \rightarrow \ _Z^A\text{X} + \text{p}
b. (\beta ^-) _1^3\text{H} \rightarrow \ _Z^A\text{X} + \text{p}
c. (\gamma) _{\;91}^{234}\text{Pa}^* \rightarrow \ _Z^A\text{X} + \text{p}
d. (\alpha) _{\;84}^{212}\text{Po} \rightarrow \ _Z^A\text{X} + \text{p}
e. (\beta ^-) _{\;6}^{14}\text{C} \rightarrow \ _Z^A\text{X} + \text{p}
f. (\alpha) _{\;79}^{172}\text{Au} \rightarrow \ _Z^A\text{X} + \text{p}
g. (\gamma) _{\;9}^{20}\text{F}^* \rightarrow \ _Z^A\text{X} + \text{p}
h. (\beta ^+) _{\;86}^{201}\text{Rn} \rightarrow \ _Z^A\text{X} + \text{p}
2. Préciser les grandeurs conservées lors de ces désintégrations.
f. (\alpha) _{\;79}^{172}\text{Au} \rightarrow \ _Z^A\text{X} + \text{p}
g. (\gamma) _{\;9}^{20}\text{F}^* \rightarrow \ _Z^A\text{X} + \text{p}
h. (\beta ^+) _{\;86}^{201}\text{Rn} \rightarrow \ _Z^A\text{X} + \text{p}
2. Préciser les grandeurs conservées lors de ces désintégrations.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Stabilité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13Vallée de la stabilité
✔ APP : Formuler des hypothèses
Le diagramme (N, Z) de Segrè représente l'ensemble des isotopes connus. On retrouve en rouge les isotopes stables, mais également les isotopes radioactifs en jaune et en bleu sur le schéma ci-dessous.
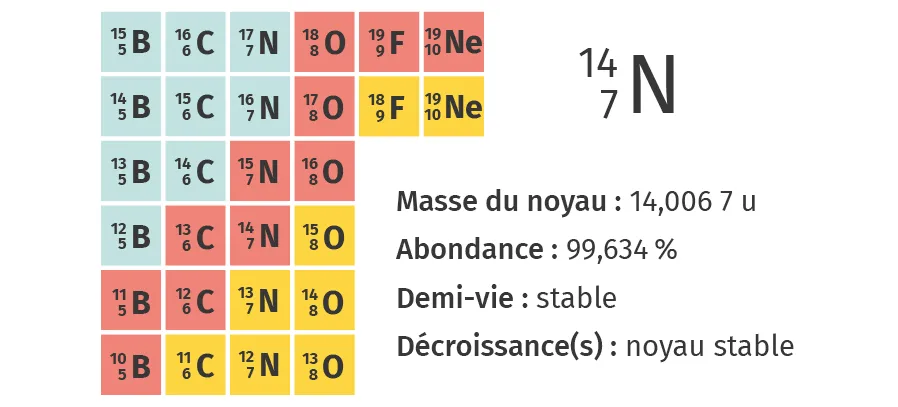
1. Définir le terme isotope.
1. Définir le terme isotope.
2. Donner la composition du noyau de chaque isotope
de l'azote.
3. En analysant leur structure, identifier quelle particule est en excès dans chacun de ces isotopes.
4. En déduire le type de radioactivité associée.
5. Expliquer le fait que les isotopes d'azote 14 et 15 représentent près de 100 % des atomes d'azote présents sur Terre.
3. En analysant leur structure, identifier quelle particule est en excès dans chacun de ces isotopes.
4. En déduire le type de radioactivité associée.
5. Expliquer le fait que les isotopes d'azote 14 et 15 représentent près de 100 % des atomes d'azote présents sur Terre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14Chaîne de désintégration
✔ APP : Maîtriser le vocabulaire du cours
Le terbium Tb est un métal malléable de la famille des lanthanides. Suite à des décharges électriques, il émet de la lumière verte qui est utilisée dans les écrans de télévision ou d'ordinateur, mais également en radiographie. L'un de ses isotopes, le terbium 152, fait l'objet d'une succession de désintégrations jusqu'à devenir stable.
1. Définir le terme radioactif.
2. Sans tenir compte d'éventuelles désintégrations \gamma, écrire les équations de désintégrations successives du terbium 152 jusqu'à ce que le noyau final obtenu soit stable.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15Uranium 235
✔ RAI/ANA : Construire un raisonnement
L'uranium 235 est un isotope naturel, il représente 0,72 % de l'uranium présent sur Terre. Souvent utilisé dans le domaine de la fission nucléaire, il peut également subir une désintégration \alpha.
1. Écrire l'équation de désintégration de l'uranium 235.
2. Déterminer le nombre de noyaux radioactifs contenu dans 3,0 g d'uranium 235.
3. Déterminer la constante radioactive \lambda.
4. En déduire son temps de demi-vie t_{1/2}.
5. Son noyau fils se désintègre à son tour en thorium. En déduire la particule émise lors de cette désintégration.
Données
- Masse molaire de l'uranium : M(^{235}\text{U}) = 235{,}0 g·mol-1
- Activité massique : A_{\text{m}} = 79{,}96 kBq·g-1
- Constante d'Avogadro : N_{\text{A}} = 6{,}02 \times 10^{23} mol-1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Loi de décroissance radioactive
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16Prométhium
✔ VAL : Exploiter un ensemble de mesures
Le prométhium 144 est un noyau radioactif de type \beta^+ dont le temps de demi-vie est égal à t_{1/2} = 1{,}0 a.
1. Écrire l'équation de désintégration de ce noyau.
2. On a un échantillon contenant 4{,}0 \times 10^{10} noyaux. Calculer le nombre de noyaux non désintégrés au bout de 0{,}5 a, 1{,}0 a, 2{,}0 a, 3{,}0 a et 4{,}0 a.
1. Écrire l'équation de désintégration de ce noyau.
2. On a un échantillon contenant 4{,}0 \times 10^{10} noyaux. Calculer le nombre de noyaux non désintégrés au bout de 0{,}5 a, 1{,}0 a, 2{,}0 a, 3{,}0 a et 4{,}0 a.
3. Tracer la courbe N = f(t).
4. Déterminer la date à laquelle il ne reste plus que 1{,}5 \times 10^{10} noyaux.
GeoGebra
4. Déterminer la date à laquelle il ne reste plus que 1{,}5 \times 10^{10} noyaux.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17Radiographie au phosphore
✔ APP : Faire des prévisions à l'aide d'un modèle
Un patient reçoit 30 ng de phosphore 32 radioactif de type \beta ^-. Les émissions \gamma émises par les noyaux fils du phosphore 32 permettent d'effectuer une radiographie.
1. Écrire l'équation de désexcitation du noyau fils.
2. Déterminer le nombre de noyaux injectés dans le patient.
1. Écrire l'équation de désexcitation du noyau fils.
2. Déterminer le nombre de noyaux injectés dans le patient.
3. Déterminer la date à laquelle 99 % des noyaux se sont désintégrés.
Données
- Masse molaire du phosphore 32 : M(^{32}\text{P}) = 32{,}0 g·mol-1
- Temps de demi-vie du phosphore 32 : t_{1/2}(^{32}\text{P}) = 14{,}26 j
- Constante d'Avogadro : N_{\text{A}} = 6{,}02 \times 10^{23} mol-1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18Bétafite
✔ RAI/ANA : Construire un raisonnement
Certains bijoux composés de cristaux de roche sont fabriqués à partir de la bétafite, un minerai contenant de l'uranium 238.
1. Préciser la particule émise lors de la désintégration \alpha de l'uranium 238.
2. Un bracelet de bétafite peut contenir jusqu'à 2,0 μg d'uranium 238. En déduire le nombre de noyaux radioactifs.
3. Exprimer l'activité d'un échantillon A en fonction de \lambda et du nombre de noyaux N.
4. Calculer l'activité radioactive d'un bracelet.
Données
- Masse molaire de l'uranium 238 : M(^{238}\text{U}) = 238{,}1 g·mol-1
- Constante radioactive de l'uranium 238 : \lambda (^{238}\text{U}) = 4{,}916 \times 10^{-18} s-1
- Constante d'Avogadro : N_{\text{A}} = 6{,}022 \times 10^{23} mol-1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19Identification de roches
✔ APP : Extraire l'information utile
Des roches radioactives ont été retrouvées dans un laboratoire. Après des analyses sur leur radioactivité, la décroissance radioactive de chacune de ces roches a été représentée ci-dessous :
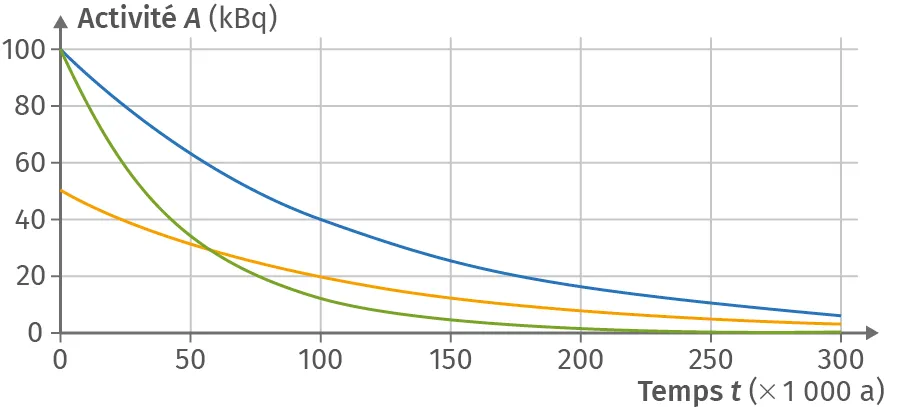
1. Définir l'activité radioactive d'un échantillon.
2. Établir la relation entre l'activité et le nombre de noyaux radioactifs présents dans l'échantillon.
3. Identifier la nature des noyaux radioactifs présents dans chacune de ces roches.
Données
Temps de demi-vie :
- t_{1/2}(^{230}\text{Th}) = 75 \times 10^3 a
- t_{1/2}(^{202}\text{Pb}) = 53 \times 10^3 a
- t_{1/2}(^{231}\text{Pa}) = 33 \times 10^3 a
- t_{1/2}(^{233}\text{U}) = 159 \times 10^3 a
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BConstante radioactive du fluor 18
✔ REA/MATH : Utiliser des outils mathématiques
Le fluor 18 ^{18}\text{F} est un isotope radioactif du fluor utilisé comme marqueur en imagerie médicale (scintigraphie). On mesure l'activité d'un échantillon de fluor 18 à l'aide d'un compteur Geiger, on trouve A = 2{,}7 \times 10^{18} Bq. On refait la mesure au bout de t = 10 h, et on obtient A' = 6{,}1 \times 10^{16} Bq.
1. Calculer la constante radioactive \lambda, puis le temps de demi‑vie t_{1/2} du fluor 18.
2. Calculer l'activité A'' d'un échantillon contenant 1 mg de fluor 18.
Le fluor 18 ^{18}\text{F} est un isotope radioactif du fluor utilisé comme marqueur en imagerie médicale (scintigraphie). On mesure l'activité d'un échantillon de fluor 18 à l'aide d'un compteur Geiger, on trouve A = 2{,}7 \times 10^{18} Bq. On refait la mesure au bout de t = 10 h, et on obtient A' = 6{,}1 \times 10^{16} Bq.
1. Calculer la constante radioactive \lambda, puis le temps de demi‑vie t_{1/2} du fluor 18.
2. Calculer l'activité A'' d'un échantillon contenant 1 mg de fluor 18.
Données
- Constante d'Avogadro : N_A = 6{,}02 \times 10^{23} mol^{-1}
- Masse molaire du fluor 18 : M_F = 18{,}0 g·mol^{-1}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une notion, trois exercicesDifférenciation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20Hydrogène radioactif
✔ REA : Appliquer une formule
Le tritium _1^3\text{H} est un isotope radioactif de l'hydrogène.
1. Définir le terme isotope.
2. Calculer le nombre de noyaux de tritium contenus dans 1,0 g de cet isotope.
3. En déduire l'activité radioactive correspondante.
Donnée
- Masse molaire du tritium : M(^3\text{H}) = 3{,}0 g·mol-1
- Constante radioactive du tritium : \lambda = 1{,}78 \times 10^{-9} s-1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21Activité du radon
✔ REA/MATH : Utiliser des outils mathématiques
1. Une roche contient 3,5 μg de radon 222. Déterminer le nombre de noyaux radioactifs N_0 dans la roche.
2. Rappeler la définition du temps de demi-vie et déterminer la constante radioactive associée.
3. Déterminer le nombre de noyaux N toujours présents au bout de 30 ans. En déduire l'activité de cette roche.
4. Déterminer l'activité de cette roche après 30 ans.
Donnée
- Masse molaire du radon 222 : M(^{222}\text{Rn}) = 222{,}0 g·mol-1
- Temps de demi-vie du radon 222 : t_{1/2}(^{222}\text{Rn}) = 3{,}82 j
- Temps de demi-vie du radium 226 : t_{1/2}(^{226}\text{Ra}) = 1\ 600 a
- Constante d'Avogadro : N_{\text{A}} = 6{,}02 \times 10^{23} mol-1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22Dangers du radium
✔ APP : Faire des prévisions à l'aide d'un modèle
Après la découverte d'une petite nappe phréatique, une contamination au radium 226 est mise en évidence.
Les analyses montrent une population de noyaux radioactifs de 8{,}01 \times 10^{13} noyaux par m3, l'activité volumique maximale autorisée étant de 1 000 Bq·m-3.
Déterminer la durée nécessaire afin que l'eau ne soit plus contaminée.
Les analyses montrent une population de noyaux radioactifs de 8{,}01 \times 10^{13} noyaux par m3, l'activité volumique maximale autorisée étant de 1 000 Bq·m-3.
Déterminer la durée nécessaire afin que l'eau ne soit plus contaminée.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
