Le « problème des tiroirs »

1. Reproduire la feuille de calcul ci‑dessous dans un tableur.


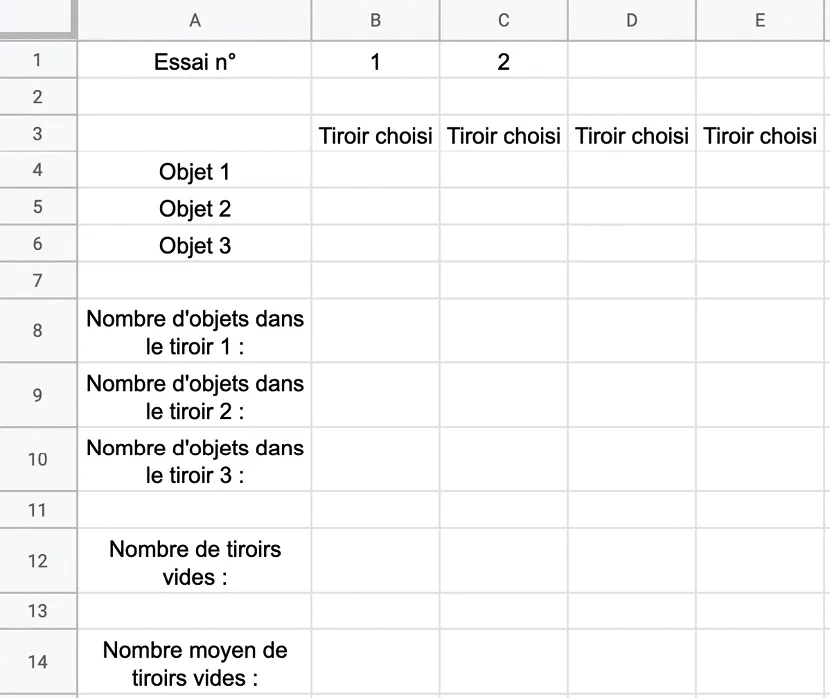
2. On souhaite réaliser 100 fois l'expérience. Compléter la ligne 1.

3. Les objets sont distribués au hasard dans les trois tiroirs. Simuler, pour chaque objet, le tiroir choisi à chaque essai.

4. On souhaite compter, à chaque essai, le nombre d'objets dans chaque tiroir. Compléter alors les lignes 8, 9 et 10.

5. Compléter alors la ligne 12, donnant le nombre de tiroirs vides parmi les trois tiroirs de la commode.

6. En déduire le nombre moyen de tiroirs vides à l'issue des 100 répétitions de l'expérience.

On considère le programme suivant.

from random import *

def tiroirs():
	L = [0,0,0]
	for i in range(3):
		k = randint(0,2)
		L[k]=L[k]+1
	return L

def nombre_tiroirs_vides():
	L = tiroirs()
	n = 0
	for k in range(3):
		if L[k]==0:
			n=n+1
	return n

def moyenne_pour_m_essais(m):
	S = 0
	for k in range(m):
		S = S + nombre_tiroirs_vides()
	return S/m

1. En ligne 4, la liste définie correspond au nombre d'objets présents dans les tiroirs 1, 2 et 3 au début de l'expérience. Expliquer la suite du programme.

2. On considère la fonction nombre_tiroirs_vides.
En ligne 11, on définit une liste L donnant la répartition du nombre d'objets dans chacun des trois tiroirs et en ligne 12, on définit une variable de comptage n valant initialement 0. Expliquer la suite du programme.

3. On s'intéresse maintenant à la fonction moyenne_pour_m_essais.
Expliquer cette fonction puis tester le programme complet pour les valeurs m = 100 puis m = 10000. Interpréter les résultats obtenus.