Chapitre 7
Fiche de révision
Compléments sur la dérivation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'essentiel
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Soient \boldsymbol{u} une fonction définie et dérivable sur un intervalle \boldsymbol{\mathrm{I}} à valeurs dans \boldsymbol{\mathrm{J}} et \boldsymbol{v} une fonction définie et dérivable sur \boldsymbol{\mathrm{J}}. Alors la fonction \boldsymbol{v \circ u} est dérivable sur \boldsymbol{\mathrm{I}} et, pour tout \boldsymbol{x_0 \in \mathrm{I}}, on a : \boldsymbol{(v \circ u)^{\prime} (x_{0})}\boldsymbol{=u^{\prime} (x_{0}) \times (v^{\prime} \circ u) (x_{0}).} Cela permet de :
✔ calculer la dérivée de fonctions composées ;
✔ étudier des fonctions composées.
2
Soit \boldsymbol{f} une fonction dérivable sur un intervalle \boldsymbol{\mathrm{I}}. \boldsymbol{f} est convexe sur \boldsymbol{\mathrm{I}} si, et seulement si, \boldsymbol{f^\prime} est croissante sur \boldsymbol{\mathrm{I}}. Cela permet de :
✔ déterminer la convexité d'une fonction ;
✔ étudier la position d'une courbe par rapport à ses tangentes ou ses sécantes ;
✔ déterminer les abscisses des éventuels points d'inflexion.
3
Soit \boldsymbol{f} une fonction dérivable sur un intervalle \boldsymbol{\mathrm{I}} dont la dérivée \boldsymbol{f^\prime} est dérivable sur \boldsymbol{\mathrm{I}}. \boldsymbol{f} est convexe sur \boldsymbol{\mathrm{I}} si, et seulement si, \boldsymbol{f^{\prime\prime}} est positive sur \boldsymbol{\mathrm{I}}. Cela permet de :
✔ déterminer la convexité d'une fonction deux fois dérivable ;
✔ étudier la position d'une courbe par rapport à ses tangentes ou ses sécantes ;
✔ déterminer les abscisses des éventuels points d'inflexion.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
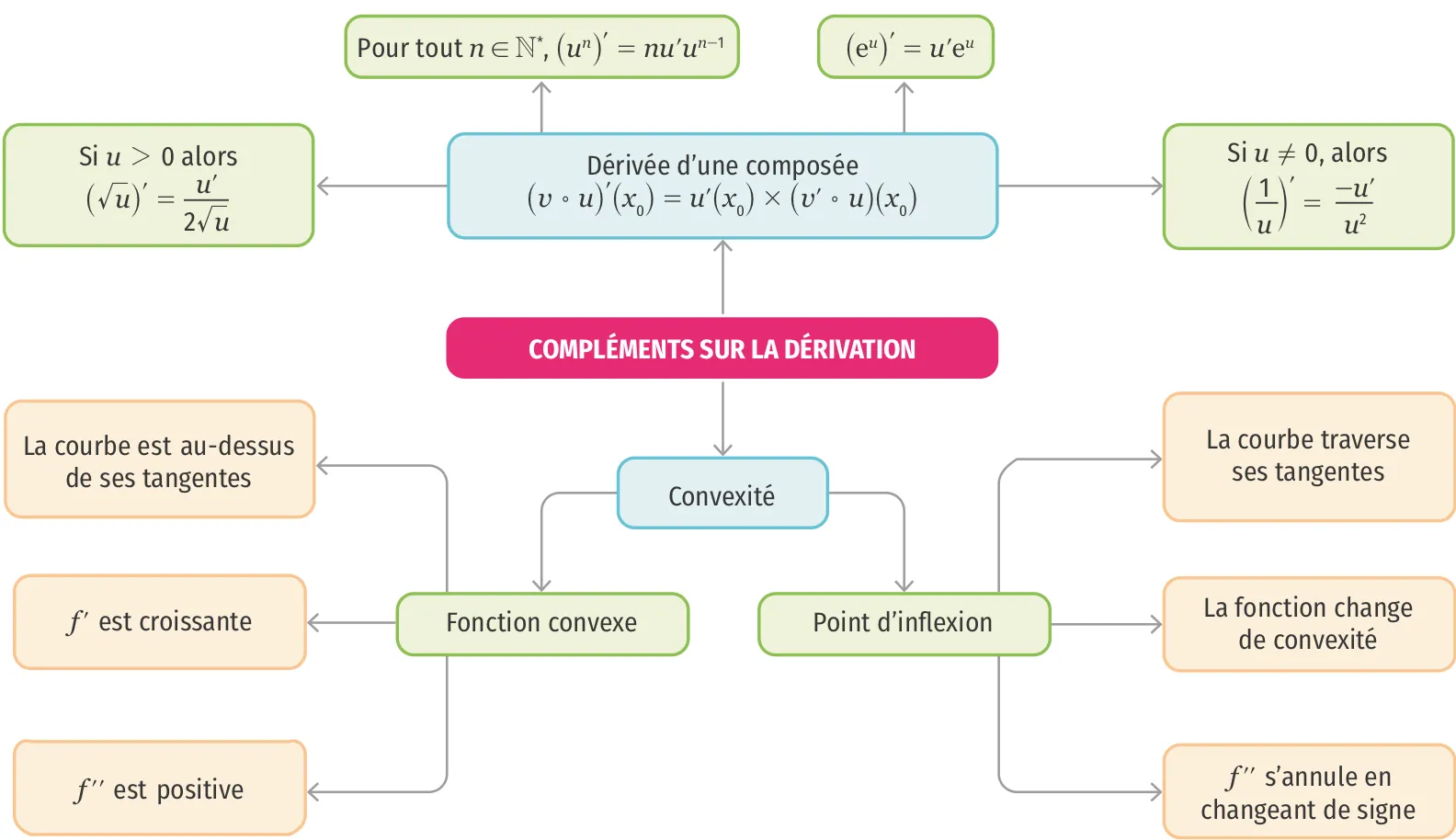
Carte mentale

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

