PRÉPARER LE

97

[D’après bac S, Pondichéry, 2003]
On considère la fonction $f$ définie sur $\mathbb{R}$ par : $f(x)=x^{2} \mathrm{e}^{x-1}-\dfrac{x^{2}}{2}$.

Partie A : Conjectures

Le graphique ci‑dessous est la courbe représentative de cette fonction telle que l’affiche une calculatrice dans un repère orthogonal.

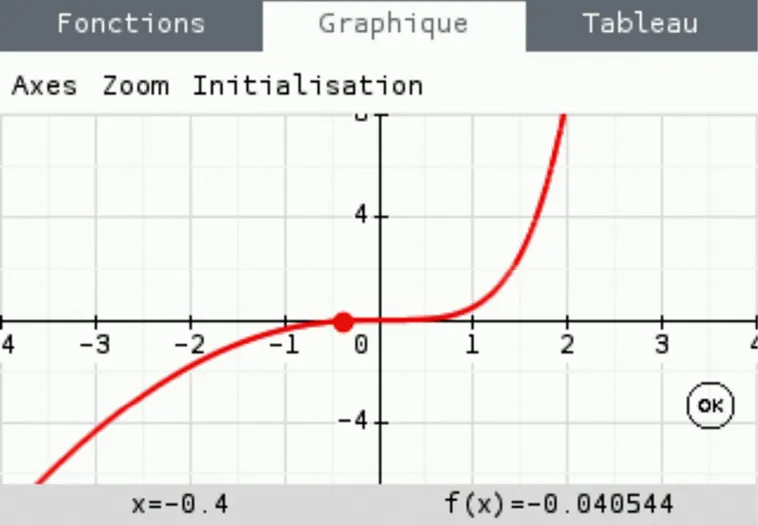
1. Conjecturer le sens de variation de $f$ sur $[-4\,; 2]$.

Effacer tout

Couleurs

Formes

Dessinez ici

2. Conjecturer le signe de $f(x)$ sur $[-4\,; 2]$.




Partie B : Étude d’une fonction auxiliaire



On définit la fonction $g$ sur $\mathbb{R}$ par $g(x)=(x+2) \mathrm{e}^{x-1}-1$.

1. Calculer $g^\prime(x)$.




2. Étudier le signe de $g^\prime(x)$ sur $[-4\,; 2]$.




3. Dresser le tableau de variations de $g$ sur $[-4\,; 2]$.

Effacer tout

Couleurs

Formes

Dessinez ici

4. On admet que $g(x) = 0$ admet une unique solution $\alpha$ dans $\mathbb{R}$ et que $0{,}20 \lt \alpha \lt 0{,}21$.
Déterminer le signe de $g(x)$ suivant les valeurs de $x$.




Partie C : Étude de la fonction $\boldsymbol{f}$

1. Déterminer $f^\prime(x)$ pour tout réel $x$.


2. Exprimer $f^\prime(x)$ en fonction de $g(x)$.


3. En déduire le signe de $f^\prime(x)$ sur $[-4\,; 2]$.




4. Dresser le tableau de variations de $f$ sur $[-4\,; 2]$.

Effacer tout

Couleurs

Formes

Dessinez ici

5. Ces résultats valident‑ils les conjectures de la partie A ?

98

[D’après bac ES, Antilles-Guyane, septembre 2019]
On donne ci‑dessous la courbe $\mathcal{C}$ représentative d’une fonction $f$ définie et dérivable sur l’intervalle $[0\,; 3]$. On note $f^\prime$ la fonction dérivée de $f$.
La droite $\mathcal{D}$ est la tangente à la courbe $\mathcal{C}$ au point d’abscisse $0$. Elle passe par le point $\text{A}$ de coordonnées $(0{,}5\,; 1)$ et par l’origine du repère.
La tangente $\text{T}$ à la courbe $\mathcal{C}$ au point d’abscisse $1$ est parallèle à l’axe des abscisses.

Partie A
Dans cette partie les réponses seront obtenues par lecture graphique.

1. Déterminer une équation de la droite $\mathcal{D}$.


2. Donner la valeur de $f^{\prime}(1)$. Justifier.


3. Proposer un intervalle sur lequel la fonction semble concave.


Partie B
La fonction $f$ est définie sur l’intervalle $[0\,; 3]$ par $f(x)=2 x \mathrm{e}^{-0,5 x^{2}}$. On note $f^\prime$ la fonction dérivée de $f$ sur l’intervalle $[0\,; 3]$.

1. Montrer que, pour tout $x \in[0\,; 3]$ : $f^{\prime}(x)=\left(2-2 x^{2}\right) \mathrm{e}^{-0,5 x^{2}}$.

2. Étudier les variations de la fonction $f$ sur l’intervalle $[0\,; 3]$ et dresser son tableau de variations.

Effacer tout

Couleurs

Formes

Dessinez ici

4. a. Déterminer la dérivée seconde $f^{\prime\prime}$ de $f$ et étudier son signe.


b. Étudier la convexité de $f$ sur $[0\,; 3]$.


Partie C
En Europe, les observateurs d’une maladie nécessitant une hospitalisation considèrent qu’ils peuvent modéliser par cette fonction $f$ l’évolution du nombre de lits occupés par des malades pendant les trois mois d’hiver.
Pour tout $x$ appartenant à l’intervalle $[0\,; 3]$, $f(x)$ représente le nombre de lits occupés, exprimé en million, à l’instant $x$, exprimé en mois.
Un journal affirme que cet hiver le nombre de lits occupés lors du pic de la maladie a dépassé le million.
Que dire de cette affirmation ?

99

[D’après bac STI Génie électrique, Métropole, 2004]
Partie A
On considère la fonction $f$ définie et dérivable sur $\mathbb{R}$ par $f(x)=\left(a x^{2}+b x+c\right) \mathrm{e}^{-x}$ où $a$, $b$ et $c$ désignent trois nombres réels que l’on se propose de déterminer dans cette partie.
Sur le graphique ci‑dessous, on a représenté la courbe représentative $\mathcal{C}_f$ de la fonction $f$ dans le plan muni du repère orthogonal $(\mathrm{O}\,; \overrightarrow{i}\,, \overrightarrow{j})$.

On admet que la droite $\mathcal{D}$ passe par $\text{A}$ et est tangente à la courbe $\mathcal{C}_f$ au point $\text{B}$.

1. a. À l’aide d’une lecture graphique, déterminer les coordonnées entières des points $\text{A}$ et $\text{B}$.
En déduire $f(-3)$ et $f(0)$.


b. Montrer qu’une équation de la droite $(\mathrm{AB})$ est $y = x + 3$. En déduire la valeur de $f^{\prime}(0)$.


2. a. Montrer que, pour tout $x$ appartenant à $\mathbb{R}$, $f^{\prime}(x)=\left[-a x^{2}+(2 a-b) x+b-c\right] \mathrm{e}^{-x}$.


b. En déduire $f^\prime(0)$, en fonction de $b$ et $c$.


3. a. En utilisant les questions précédentes, montrer que les réels $a$, $b$ et $c$ sont solutions du système : $\left\{\begin{aligned} 9 a-3 b+c &=0 \\ b-c &=1 \\ c &=3 \end{aligned}\right.$.

b. Résoudre le système et en déduire l’expression de $f(x)$ en fonction de $x$.


Partie B On suppose que $f$ est définie sur $\mathbb{R}$ par : $f(x)=\left(x^{2}+4 x+3\right) \mathrm{e}^{-x}$.
1. Vérifier que, pour tout réel $x$, $f^{\prime}(x)=\left(-x^{2}-2 x+1\right) \mathrm{e}^{-x}$.


2. Pour tout réel $x$, étudier le signe de $f^\prime(x)$ et dresser le tableau de variations de la fonction $f$ sur $\mathbb{R}$.

Effacer tout

Couleurs

Formes

Dessinez ici

3. Calculer une valeur approchée à $10^{-1}$ près de l’ordonnée de chacun des points de la courbe $\mathcal{C}_f$ où la tangente est parallèle à l’axe des abscisses.