1. \|\vec{u}\|=8,\|\vec{v}\|=3 et \theta=60^{\circ}.

2. \|\vec{u}\|=2,\|\vec{v}\|=1 et \theta=135^{\circ}.

3. \|\vec{u}\|=\frac{2}{5},\|\vec{v}\|=\frac{5}{6} et \theta=0^{\circ}.

1. \|\vec{u}\|=3,\|\vec{v}\|=2 et \theta=\frac{7 \pi}{6}.

2. \|\vec{u}\|=5,\|\vec{v}\|=9 et \theta=\frac{5 \pi}{2}.

3. \|\vec{u}\|=\sqrt{3},\|\vec{v}\|=7 et \theta=-\frac{5 \pi}{6}.

4. \|\vec{u}\|=\frac{2}{9},\|\vec{v}\|=\frac{\sqrt{3}}{3} et \theta=\frac{4 \pi}{3}.

1. \|\vec{u}\|=3-\sqrt{5},\|\vec{v}\|=3+\sqrt{5} et \theta=\frac{\pi}{3}.

2. \|\vec{u}\|=\frac{2}{2+\sqrt{3}},\|\vec{v}\|=2-\sqrt{3} et \theta=-\frac{2 \pi}{3}.

Dans chaque cas, déterminer la valeur en degré, arrondie éventuellement à 0,01 près, de l'angle \theta entre \vec{u} et \vec{v}.

1. \|\vec{u}\|=6,\|\vec{v}\|=3 et \vec{u} \cdot \vec{v}=-4.

2. \|\vec{u}\|=2,\|\vec{v}\|=\sqrt{3} et \vec{u} \cdot \vec{v}=0.

3. \|\vec{u}\|=4,\|\vec{v}\|=3 et \vec{u} \cdot \vec{v}=2.

Consigne

Pour les

exercices 70

à

72

Soient \text{A}, \text{B} et \text{C} trois points du plan.

Calculer \overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{AC}} dans chaque cas.

1. \mathrm{AB}=4, \mathrm{AC}=6 et \widehat{\mathrm{BAC}}=\frac{5 \pi}{6}.

2. \mathrm{AB}=\frac{4}{3}, \mathrm{AC}=\frac{3}{2} et \widehat{\mathrm{BAC}}=\frac{3 \pi}{4}.

Les premières apparitions du produit scalaire ont lieu en 1843 dans les écrits de Sir William Rowan Hamilton. C'est vers 1880 que la notation \cdot est utilisée par Josiah Willard Gibbs. Cet outil est né de problèmes physiques à résoudre.

Calculer \overrightarrow{\mathrm{BA}} \cdot \overrightarrow{\mathrm{BC}} dans chaque cas.

1. \mathrm{AB}=6, \mathrm{CB}=5 et \widehat{\mathrm{ABC}}=\frac{2 \pi}{6}.

2. \mathrm{BA}=\frac{5}{3}, \mathrm{CB}=4 et \widehat{\mathrm{ABC}}=\frac{9 \pi}{4}.

1. \mathrm{AB}=9, \mathrm{AC}=2 et \widehat{\mathrm{BAC}}=\frac{3 \pi}{4}. Calculer \overrightarrow{\mathrm{BA}} \cdot \overrightarrow{\mathrm{AC}}.

2. \mathrm{AC}=\sqrt{3}, \mathrm{BC}=5 et \widehat{\mathrm{ACB}}=\frac{\pi}{6}. Calculer \overrightarrow{\mathrm{BC}} \cdot \overrightarrow{\mathrm{CA}}.

Soient \vec{u} et \vec{v} deux vecteurs colinéaires. On suppose que \|\vec{u}\|=3. Dans chaque cas, calculer \vec{u} \cdot \vec{v}.

1. \vec{v}=2 \vec{u}

2. \vec{v}=-\frac{3}{5} \vec{u}

3. \vec{u}=-5 \vec{v}

4. \vec{u}=\frac{2}{7} \vec{v}

Calculer les produits scalaires suivants.

1. \overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{BE}}

2. \overrightarrow{\mathrm{FD}} \cdot \overrightarrow{\mathrm{CF}}

3. \overrightarrow{\mathrm{HG}} \cdot \overrightarrow{\mathrm{BD}}

4. \overrightarrow{\mathrm{DG}} \cdot \overrightarrow{\mathrm{DE}}

Calculer les produits scalaires suivants.

1. \left(\frac{1}{2} \overrightarrow{\mathrm{FE}}\right) \cdot \overrightarrow{\mathrm{DB}}

2. \left(-\frac{2}{3} \overrightarrow{\mathrm{DH}}\right) \cdot\left(\frac{6}{5} \overrightarrow{\mathrm{CE}}\right)

3. \overrightarrow{\mathrm{GE}} \cdot(-3 \overrightarrow{\mathrm{AB}})

4. (2 \overrightarrow{\mathrm{AB}}) \cdot(-5 \overrightarrow{\mathrm{GH}})

Soient \text{ABCD} et \text{BCEF} deux carrés de côté 2.


Parmi les produits scalaires suivants, lesquels sont nuls ?

1. \overrightarrow{\mathrm{BC}} \cdot \overrightarrow{\mathrm{EF}}

2. \overrightarrow{\mathrm{AD}} \cdot \overrightarrow{\mathrm{CD}}

3. \overrightarrow{\mathrm{EF}} \cdot \overrightarrow{\mathrm{FE}}

4. \overrightarrow{\mathrm{BF}} \cdot \overrightarrow{\mathrm{DA}}

5. \overrightarrow{\mathrm{CE}} \cdot \overrightarrow{\mathrm{EF}}

6. \overrightarrow{\mathrm{BE}} \cdot \overrightarrow{\mathrm{BD}}

On se place dans un repère orthonormé (\mathrm{O} \: ; \vec{i}, \vec{j}) et on considère \vec{u}\left(\begin{array}{l} x \\ y \end{array}\right), \vec{v}\left(\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right) et \vec{w}\left(\begin{array}{l} x^{\prime \prime} \\ y^{\prime \prime} \end{array}\right).

En utilisant la formule \vec{u} \cdot \vec{v}=x x^{\prime}+y y^{\prime}, redémontrer les égalités suivantes.

1. \vec{u} \cdot \vec{v}=\vec{v} \cdot \vec{u} et (-\vec{u}) \cdot \vec{v}=-\vec{u} \cdot \vec{v}.

2. (k \vec{u}) \cdot \vec{v}=k \times \vec{u} \cdot \vec{v}, où k désigne un réel.

3. (\vec{u}+\vec{v}) \cdot \vec{w}=\vec{u} \cdot \vec{w}+\vec{v} \cdot \vec{w}

Soient \mathrm{A}, \mathrm{B} et \text{C} trois points du plan muni d'un repère orthonormé.
Dans chaque cas, calculer \overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{AC}}, puis déterminer une mesure en degré, arrondie à 10^{-2} près, de l'angle \widehat{\mathrm{BAC}}.

1. \mathrm{A}(-3 \: ;-1), \mathrm{B}(1 \: ; 2) et \mathrm{C}(2 \: ; 1).

2. \mathrm{A}(2 \: ; 2), \mathrm{B}(6 \: ;-1) et \mathrm{C}(5 \: ; 3).

Soient \mathrm{A}, \mathrm{B} et \text{C} trois points du plan muni d'un repère orthonormé.
Dans chaque cas, calculer \overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{AC}}, puis déterminer une mesure exacte en radian de l'angle \widehat{\mathrm{BAC}}.

1. \mathrm{A}(3 \: ; 2), \mathrm{B}(8 \: ; 1) et \mathrm{C}(6 \: ; 4).

2. \mathrm{A}(3 \: ; 2), \mathrm{B}(5 \: ; 2) et \mathrm{C}(1 \: ; 2+2 \sqrt{3}).

3. \mathrm{A}(1 \: ; 1), \mathrm{B}(2 \sqrt{3}+1 \: ; 3) et \mathrm{C}(6 \: ; 5 \sqrt{3}+1).

Dans un repère orthonormé, on considère les vecteurs \vec{u}\left(\begin{array}{l} n \\ 2 \end{array}\right) et \vec{v}\left(\begin{array}{c} 4-n \\ n \end{array}\right), où n désigne un entier naturel.

1. Démontrer que \vec{u} \cdot \vec{v}=-n^{2}+6 n.

2. a. À l'aide d'une calculatrice, dresser le tableau de valeurs de \vec{u} \cdot \vec{v} pour n variant de 0 à 10 avec un pas de 1.

b. Conjecturer alors la valeur de n pour laquelle \vec{u} \cdot \vec{v}=9.

c. Démontrer la conjecture.

Le travail \text{W}, en joule, d'une force \overrightarrow{\mathrm{F}}, en newton, lors d'un déplacement rectiligne \text{AB}, en mètre, est défini par \mathrm{W}=\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{AB}}.

Vincent et sa fille Anissa partent en balade à vélo équipés d'une remorque pour enfants. Vincent doit monter une côte de 2 km, faisant une pente de \frac{\pi}{12} \: \mathrm{rad} avec l'horizontale.

Le zoom est accessible dans la version Premium.

Découvrir l'offre premium

La traction du vélo sur la remorque est représentée par une force \overrightarrow{\mathrm{F}} d'intensité 700 newtons. Cette force forme un angle de \frac{5 \pi}{36} \: \mathrm{rad} avec l'horizontale.

Calculer le travail de cette force sur ce parcours.

Dans un repère orthonormé, on considère les vecteurs \vec{u}\left(\begin{array}{l} x \\ 4 \end{array}\right) et \vec{v}\left(\begin{array}{c} x \\ -1 \end{array}\right), où x désigne un entier relatif.

1. a. Reproduire dans un tableur le tableau suivant. Les colonnes \bf{A} et \bf{B} représentent les coordonnées de \vec{u} et les colonnes \bf{C} et \bf{D} représentent les coordonnées de \vec{v}.

Le zoom est accessible dans la version Premium.

Découvrir l'offre premium

b. Compléter les cellules \bf{B2} et \bf{D2}. Quelles formules doit‑on saisir dans les cellules \bf{C2} et \bf{E2} ?

c. En étirant les formules des colonnes \bf{A} à \bf{E}, conjecturer les valeurs de x pour lesquelles \vec{u} \cdot \vec{v}=0.

2. Démontrer cette conjecture.

Dans un repère orthonormé, on considère les vecteurs \vec{u}\left(\begin{array}{l} x \\ y \end{array}\right) et \vec{v}\left(\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right).

1. Reproduire dans un tableur le tableau suivant.


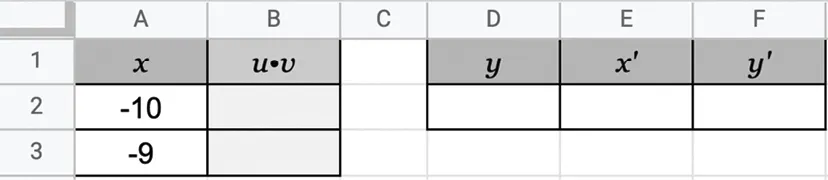
2. On choisit ici y=2, x^{\prime}=3 et y^{\prime}=-3.

a. Compléter les cellules \bf{D2}, \bf{E2} et \bf{F2}.

b. Quelle formule doit‑on saisir dans la cellule \bf{B2} afin d'y faire apparaître la valeur de \vec{u} \cdot \vec{v} ?

c. En étirant la formule de la cellule \bf{B2}, conjecturer la valeur de x pour laquelle \vec{u} \cdot \vec{v}=0.

d. Démontrer cette conjecture.

3. On choisit maintenant y=-3, x^{\prime}=-4 et y^{\prime}=-8.

a. Modifier le tableur afin de conjecturer la valeur de x pour laquelle \vec{u} \cdot \vec{v}=0.

b. Démontrer cette conjecture.

Donner la norme de deux vecteurs non colinéaires, \vec{u} et \vec{v} et une mesure de l'angle (\vec{u}\:, \vec{v}) de façon à ce que \vec{u} \cdot \vec{v}=36 \sqrt{3}.

Dans un repère orthonormé, on considère les vecteurs \vec{u}\left(\begin{array}{l} x \\ y \end{array}\right) et \vec{v}\left(\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right).

Déterminer des coordonnées possibles de \vec{u} et \vec{v} non colinéaires tels que \vec{u} \cdot \vec{v}=-50.