Annuler le travail d'une force

Le travail $\text{W},$ exprimé en joule, d'une force $\overrightarrow{\text{F}},$ en newton, sur un déplacement rectiligne $\overrightarrow{\mathrm{AB}},$ en mètre, est défini par $\text{W}=\overrightarrow{\mathrm{F}}\cdot \overrightarrow{\mathrm{AB}}.$

Dans un repère orthonormé, on considère trois points $\mathrm{A}(1;16),\mathrm{B}(-7;18)$ et ${\mathrm{F}}_n\left(n;n^2-20\right)$, où $n$ désigne un entier naturel.

On souhaite déterminer la valeur de $\mathbf{n}$ pour laquelle le travail de la force $\overrightarrow{{\mathbf{AF}}_{\mathbf{n}}}$ lors du déplacement $\overrightarrow{\mathbf{AB}}$ est nul, en utilisant une des trois méthodes.

1. Calculer les coordonnées de $\overrightarrow{\mathrm{AB}},$ puis exprimer les coordonnées de $\overrightarrow{{\mathrm{AF}}_n}$ en fonction de $n.$

2.  En déduire que $\mathrm{W}=2n^2-8n-64.$

3. Voici ci‑dessous un programme écrit en langage Python.

from math import*
n = 0
p = -64
while ... :
  n = n + 1
  p = ...
y = n**2 - 20
print(n)
print(y)

a. Justifier la ligne 3 du programme.

b. Que doit‑on saisir en lignes 4 et 6 pour que cet algorithme affiche la valeur de $n$ pour laquelle $\text{W}$ est nul ?

c. À quoi correspond la valeur $y$ affichée en fin d'algorithme ?

4. Saisir et lancer cet algorithme. Donner la valeur de $n$ telle que le travail soit nul, puis donner les coordonnées de ${\mathrm{F}}_n$ correspondantes.

1. Reproduire la feuille de calcul suivante et compléter les cellules $B1$, $B2$, $D1$ et $D2$.

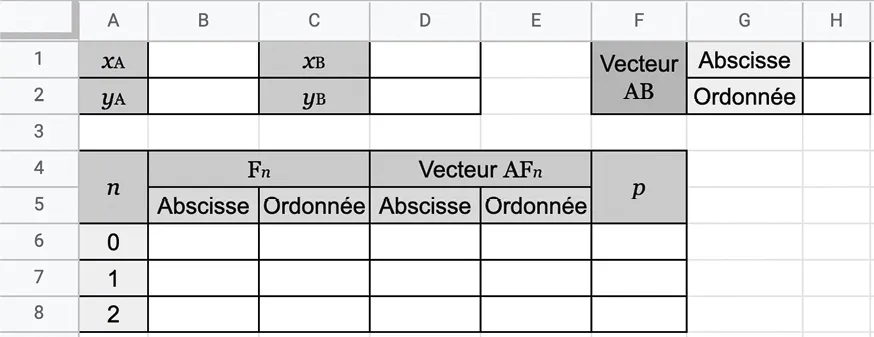
2. Quelles formules doit‑on saisir dans les cellules $H1$ et $H2$ pour calculer les coordonnées de $\overrightarrow{\mathrm{AB}}$ ?

3. a. Quelles formules faut‑il saisir et étirer vers le bas dans les cellules $B6$ et $C6$ pour calculer les coordonnées de ${\mathrm{F}}_n$ ?

b. Quelles formules faut‑il saisir et étirer vers le bas dans les cellules $D6$ et $E6$ pour calculer les coordonnées de $\overrightarrow{{\mathrm{AF}}_n}$ ?

4. Dans la cellule $F6$, saisir la formule $=\$H\$1^{\ast }D6+\$H\$2^{\ast }E6$. Que calcule‑t‑elle ? Expliquer les $\$$ présents dans la formule.

5. Déterminer la valeur de $n$ telle que le travail soit nul, puis donner les coordonnées de ${\mathrm{F}}_n$ correspondantes.

1. Placer les points $\text{A}$ et $\text{B},$ créer un curseur $n$ variant de $0$ à $30$ avec un incrément de $1,$ puis créer le point ${\mathrm{F}}_n.$

2. Définir les vecteurs $u=\overrightarrow{\mathrm{AB}}$ et $v=\overrightarrow{{\mathrm{AF}}_n}.$ Saisir la formule : $\mathbf{p}=\mathbf{x}(\mathbf{u})\mathbf{x}(\mathbf{v})+\mathbf{y}(\mathbf{u})\mathbf{y}(\mathbf{v})$.
À quoi correspond $\mathbf{p}$ dans cet exercice ?

3. a. En faisant varier $n,$ déterminer la valeur de $n$ pour laquelle le travail est nul.

b. Pour quelles coordonnées de ${\mathrm{F}}_n$ le travail de la force $\overrightarrow{{\mathrm{AF}}_n}$ est‑il nul ?

Concrètement, le travail d'une force sur un déplacement rectiligne correspond à l'énergie qu'elle produit lorsque le point d'application (souvent le centre de gravité du système étudié) se déplace selon un vecteur $\overrightarrow{\mathrm{AB}}.$

On peut remarquer que la définition du travail d'une force diffère de la définition usuelle du mot « travail ». Par exemple, le travail d'une force dont le point d'application ne travaille pas est nul ($\overrightarrow{\mathrm{AB}}=\overrightarrow{0}$).

Mais si on tient sans bouger et à bout de bras un objet, la force qu'on exerce sur cet objet aura un travail nul, bien que nous ressentions un certain épuisement au bout d'un moment.