Thème 1 : Une longue histoire de la matière
Ch. 1
Les éléments chimiques
Ch. 2
Des édifices ordonnés : les cristaux
Ch. 3
Une structure complexe : la cellule
Thème 2 : Le Soleil, notre source d'énergie
Ch. 4
Le rayonnement solaire
Ch. 5
Le bilan radiatif terrestre
Ch. 6
Énergie solaire et photosynthèse
Ch. 7
Le bilan thermique du corps humain
Thème 3 : La Terre, un astre singulier
Ch. 8
La forme de la Terre
Ch. 9
L'histoire de l’âge de la Terre
Ch. 10
La Terre dans l’Univers
Thème 4 : Son et musique, porteurs d'information
Ch. 11
Le son, phénomène vibratoire
Ch. 12
Musique et nombres
Ch. 13
Le son, une information à coder
Ch. 14
Entendre la musique
Projet Experimental et Numérique
Livret Maths
Annexes
Chapitre 4
Exercices
Le coin des experts
11 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9La loi de Stefan-Boltzmann
✔ Saisir des informations et les mettre en relation
La loi de Stefan-Boltzmann permet de calculer la puissance surfacique émise par un astre en fonction de sa température de surface. Cette loi, accompagnée de la loi de Wien et de l'information du rayon de l'astre, permet aux astrophysiciens de calculer la puissance du rayonnement émis par les étoiles.
La loi de Stefan-Boltzmann s'écrit sous la forme :
On peut trouver la puissance de rayonnement de l'étoile en multipliant la puissance surfacique par la surface de l'étoile.
On rappelle la loi de Wien, s'appliquant à un corps noir de température de surface T et de longueur d'onde d'émission maximale \lambda_{\max } :
La loi de Stefan-Boltzmann permet de calculer la puissance surfacique émise par un astre en fonction de sa température de surface. Cette loi, accompagnée de la loi de Wien et de l'information du rayon de l'astre, permet aux astrophysiciens de calculer la puissance du rayonnement émis par les étoiles.
La loi de Stefan-Boltzmann s'écrit sous la forme :
P_{\text { surface }}=\sigma \cdot T^{4} où T est la température de surface en kelvin (K).
P est la puissance surfacique en W·m-2 et
\sigma=5\text{,}67 \times 10^{-8} W·m-2·K-4.
P est la puissance surfacique en W·m-2 et
\sigma=5\text{,}67 \times 10^{-8} W·m-2·K-4.
On peut trouver la puissance de rayonnement de l'étoile en multipliant la puissance surfacique par la surface de l'étoile.
On rappelle la loi de Wien, s'appliquant à un corps noir de température de surface T et de longueur d'onde d'émission maximale \lambda_{\max } :
k_{\text { Wien }}=2\text{,}898 \times 10^{-3} m·K
1. En considérant le Soleil comme un corps noir, calculez sa température de surface.
2. À l'aide de la loi de Stefan-Boltzmann, calculez la puissance surfacique du rayonnement solaire.
3. Déduisez des calculs précédents et de l'énoncé la puissance du rayonnement solaire. Comparez la valeur obtenue avec celle donnée dans .
3. Déduisez des calculs précédents et de l'énoncé la puissance du rayonnement solaire. Comparez la valeur obtenue avec celle donnée dans .
Doc. 1
Propriétés géométriques d'une sphère.
Le zoom est accessible dans la version Premium.
Doc. 2
Spectre d'émission du Soleil.
Le zoom est accessible dans la version Premium.
Doc. 3
Carte d'identité du Soleil.
Le zoom est accessible dans la version Premium.
Circonférence équatoriale : 4\text{,}379 \times 10^{6} km
Masse : 1\text{,}989 \times 10^{30} kg
Densité : 1\text{,}409 g·cm-3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10Des ensoleillements journaliers différents
✔ Interpréter des résultats et en tirer des conclusions. Identifier des outils et les mettre en oeuvre dans une démarche scientifique
Nîmes (France) et Uccle (Belgique) sont deux villes ayant la même longitude mais des latitudes différentes. On cherche à comparer les ensoleillements de ces deux villes.
Nîmes (France) et Uccle (Belgique) sont deux villes ayant la même longitude mais des latitudes différentes. On cherche à comparer les ensoleillements de ces deux villes.
1. Expliquez l'intérêt de la construction d'un diagramme solaire cylindrique dans la compréhension de l'ensoleillement d'un point à la surface de la Terre. Comment relier ce diagramme à la puissance de l'énergie solaire reçue en surface ?
2. Pour la commune d'Uccle, décrivez l'évolution de l'ensoleillement au cours de l'année. Expliquez l'évolution de la hauteur solaire à partir de vos connaissances sur la position de la Terre par rapport au Soleil au cours des saisons.
3. Procédez de même pour la ville de Nîmes.
4. Proposez une méthode pour utiliser ce mode de représentation dans la comparaison des ensoleillements à des latitudes différentes.
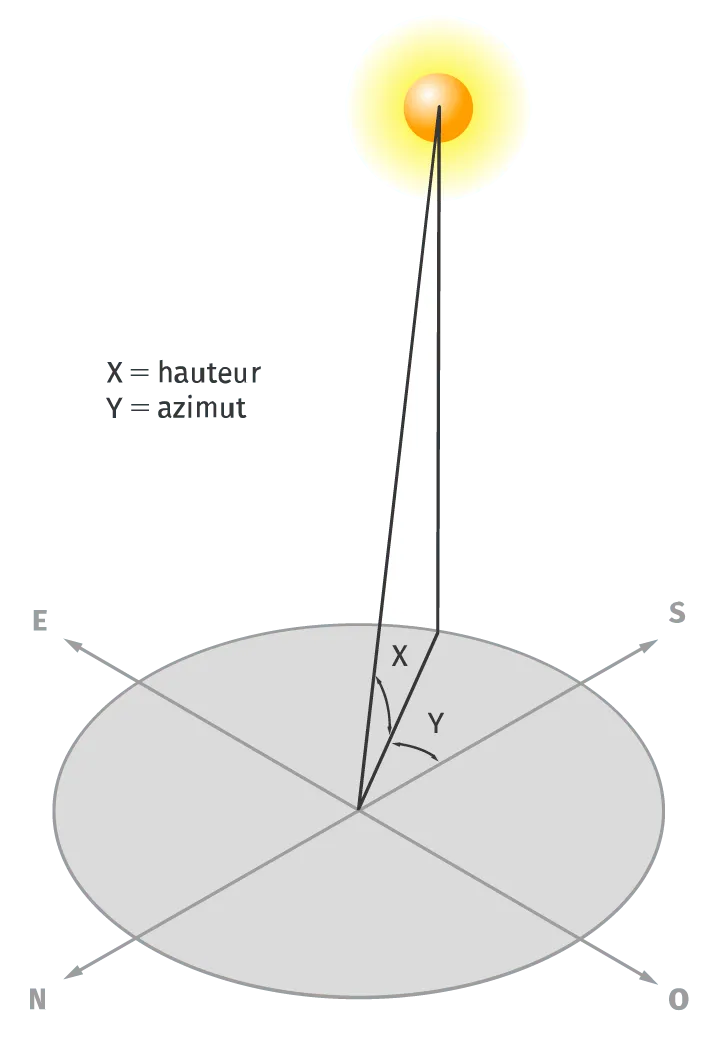
2. Pour la commune d'Uccle, décrivez l'évolution de l'ensoleillement au cours de l'année. Expliquez l'évolution de la hauteur solaire à partir de vos connaissances sur la position de la Terre par rapport au Soleil au cours des saisons.
3. Procédez de même pour la ville de Nîmes.
4. Proposez une méthode pour utiliser ce mode de représentation dans la comparaison des ensoleillements à des latitudes différentes.
Doc. 1
Définitions des paramètres utilisés pour construire un diagramme cylindrique.
Le zoom est accessible dans la version Premium.
Un diagramme solaire cylindrique est une représentation graphique permettant de visualiser la trajectoire du Soleil au cours du temps en un point donné.
Doc. 2
Diagramme solaire cylindrique pour la commune d'Uccle (Belgique).
Le zoom est accessible dans la version Premium.
Doc. 3
Diagramme solaire cylindrique pour la commune de Nîmes (France).
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CLes variations saisonnières selon les villes
✔ Traduire des informations sous forme graphique
On cherche à comprendre l'effet de la latitude sur la réception d'énergie solaire en France, à différents moments de l'année.
1. Représenter graphiquement les paramètres de façon à faciliter la lecture des résultats pour répondre à la problématique.
2. Commentez les résultats et répondez à la problématique de départ.
On cherche à comprendre l'effet de la latitude sur la réception d'énergie solaire en France, à différents moments de l'année.
1. Représenter graphiquement les paramètres de façon à faciliter la lecture des résultats pour répondre à la problématique.
Cette fonctionnalité est accessible dans la version Premium.
Cette fonctionnalité est accessible dans la version Premium.
2. Commentez les résultats et répondez à la problématique de départ.
Doc.
Tableau de relevés de certains paramètres d'ensoleillement dans différentes villes françaises.
| Ville | Latitude | Durée de la journée au solstice d'été | Hauteur du soleil à midi au solstice d'été | Durée de la journée au solstice d'hiver | Hauteur du Soleil à midi au solstice d'hiver |
| Lille | 50° 38' | 16 h 15 min | 62,8° | 7 h 45 min | 15,9° |
| Paris | 48° 50' | 15 h 48 min | 64,6° | 8 h 02 min | 17,7° |
| Dijon | 47° 19' | 15 h 44 min | 66,1° | 8 h 16 min | 19,2° |
| Lyon | 45° 46' | 15 h 32 min | 67,7° | 8 h 28 min | 20,8° |
| Bordeaux | 44° 50' | 15 h 24 min | 68,6° | 8 h 36 min | 21,7° |
| Marseille | 43° 17' | 15 h 13 min | 70,2 ° | 8 h 47 min | 23,3° |
| Ajaccio | 41° 55' | 15 h 03 min | 71,5 ° | 8 h 57 min | 24,6° |
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah