Physique-Chimie 1re Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
1. Constitution et transformations de la matière
Ch. 1
Composition chimique d'un système
Ch. 2
Composition chimique des solutions
Ch. 3
Évolution d'un système chimique
Ch. 4
Réactions d'oxydoréduction
Ch. 5
Détermination d'une quantité de matière par titrage
Livret Bac : Thème 1
Ch. 6
De la structure à la polarité d'une entité
Ch. 7
Interpréter les propriétés d’une espèce chimique
Ch. 8
Structure des entités organiques
Ch. 9
Synthèse d'espèces chimiques organiques
Ch. 10
Conversions d'énergie au cours d'une combustion
Livret Bac : Thème 1 bis
2. Mouvement et interactions
Ch. 11
Modélisation d'interactions fondamentales
Ch. 12
Description d'un fluide au repos
Ch. 13
Mouvement d'un système
Livret Bac : Thème 2
3. L'énergie, conversions et transferts
Ch. 14
Études énergétiques en électricité
Ch. 15
Études énergétiques en mécanique
Livret Bac : Th ème 3
4. Ondes et signaux
Ch. 16
Ondes mécaniques
Ch. 17
Images et couleurs
Ch. 18
Modèles ondulatoire et particulaire de la lumière
Livret Bac : Thème 4
Méthode
Fiches méthode
Fiche méthode compétences
Annexes
Chapitre 21
Exercices
Pour s'entraîner
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23Modélisation de l'œil
✔ MATH : Utiliser des outils mathématiques
On cherche à modéliser un œil au laboratoire avec une simple lentille mince convergente de distance
focale f^{\prime}= 15 cm et avec un écran. Pour un objet situé à 37,5 cm de la lentille, une image nette se forme sur l'écran.
1. Préciser quelles parties de l'œil réel sont modélisées par la lentille et par l'écran.
2. À l'aide de la relation de conjugaison, déterminer le diamètre de cet œil ainsi modélisé.
1. Préciser quelles parties de l'œil réel sont modélisées par la lentille et par l'écran.
2. À l'aide de la relation de conjugaison, déterminer le diamètre de cet œil ainsi modélisé.
3.
Faire un schéma normalisé de la situation à l'échelle 1/5, 1 carreau sur GeoGebra équivaut à 5 cm en réalité.
4. Expliquer pourquoi dans un œil réel, la relation de conjugaison donnée dans le cours n'est pas applicable pour déterminer la position de l'image.
GeoGebra
4. Expliquer pourquoi dans un œil réel, la relation de conjugaison donnée dans le cours n'est pas applicable pour déterminer la position de l'image.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
Une histoire d'éclairage en QCM
✔ RAI/ANA : Utiliser des observations
Un objet est éclairé en lumière blanche et apparaît bleu.
1. Donner la bonne réponse.
Un objet est éclairé en lumière blanche et apparaît bleu.
1. Donner la bonne réponse.
2.
Eclairé en lumière cyan, ce même objet apparaît :
3. Pour qu'il apparaisse noir, il faut l'éclairer avec de la lumière :
3. Pour qu'il apparaisse noir, il faut l'éclairer avec de la lumière :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25Match retour France-Allemagne
✔ REA : Mettre en oeuvre un protocoleSur un écran géant les drapeaux de la France et de l'Allemagne sont affichés.
Comment obtenir ces deux drapeaux sur un écran géant avec des pixels composés de trois couleurs ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
Comprendre les attendus
Des billes magiques
✔ APP : Maîtriser le vocabulaireOn considère deux billes, une de couleur cyan et une de couleur magenta (lorsqu'elles sont éclairées en lumière blanche). On possède une source de lumière blanche et des filtres colorés bleu, vert et rouge. On pose les billes sur un fond noir.
1. Si on positionne un filtre rouge devant la source de lumière blanche, de quelle couleur vont apparaître les billes ?
2. Quel filtre faut-il utiliser pour avoir les billes de la même couleur ?
3. Comment éclairer les billes pour faire disparaître la bille magenta ?
4. Est-il possible de faire disparaître les deux billes en même temps ?
Détails du barème
TOTAL /7 pts
0,5 pt
1.
Identifier la couleur obtenue grâce au filtre.0,5 pt
1.
Identifier la synthèse soustractive.1 pt
1.
Utiliser correctement la synthèse soustractive.1 pt
2.
Les billes doivent diffuser la même couleur.1 pt
2.
Identifier correctement la couleur diffusée commune.1,5 pt
3.
La bille disparaît si l'on ne peut pas la distinguer du fond.1 pt
4.
Vérifier la lumière absorbée par chaque bille et conclure.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27Quelle est cette lentille ?
✔ MATH : Utiliser des outils mathématiquesUne lentille forme sur un écran l'image d'un objet de hauteur 10,0 m. Cet objet se trouve à 50,0 m de la lentille. La taille de l'image obtenue est de 1,11 m.
1. Déterminer la position de l'image par rapport à la lentille.
2. Déterminer la distance focale de cette lentille.
3. À quelle distance de la lentille doit être l'objet pour que l'écran soit à 2,00 m de la lentille ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28Où est l'image ?
✔ MATH : Utiliser des outils mathématiquesUn objet réel est situé à 15 cm d'une lentille convergente de distance focale f^{\prime}= 20 cm.
1. À quelle distance du point focal objet se situe l'objet ?
2. À quelle distance de la lentille se trouve l'image ? Est-elle réelle ?
3. À quel instrument d'optique courant cette situation correspond-elle ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29 Démonstration du grandissement
✔ MATH : Utiliser des outils mathématiques
On exploite le schéma ci-dessous.
Les conventions sont celles utilisées dans le cours.
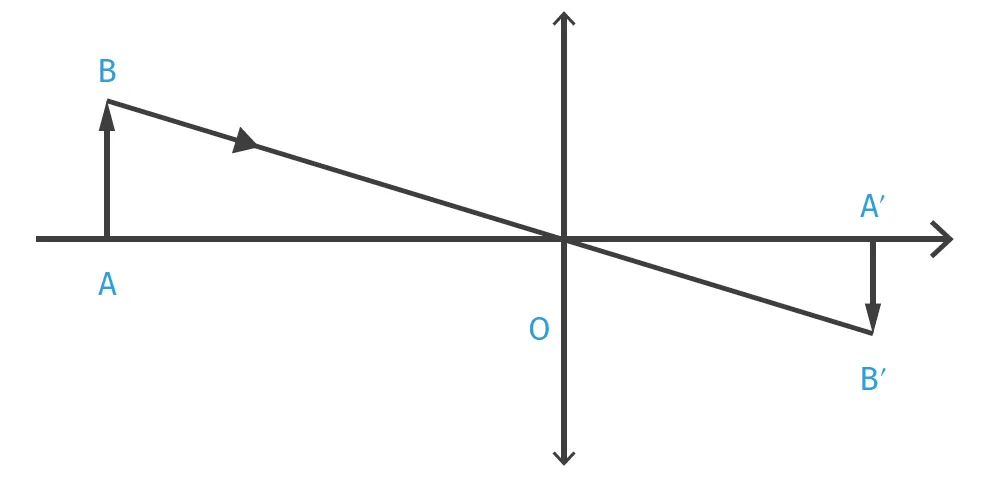
On exploite le schéma ci-dessous.
Les conventions sont celles utilisées dans le cours.
1.
Rappeler la relation de grandissement à l'aide des longueurs algébriques \overline{\mathrm{AB}} et \overline{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}.
2. Que peut-on dire des segments [\mathrm{AB}] et [\mathrm{A}^{\prime} \mathrm{B}^{\prime}] ?
3. En utilisant le théorème de Thalès donner la deuxième version de la formule du grandissement.
2. Que peut-on dire des segments [\mathrm{AB}] et [\mathrm{A}^{\prime} \mathrm{B}^{\prime}] ?
3. En utilisant le théorème de Thalès donner la deuxième version de la formule du grandissement.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30Au concert
✔ APP : Extraire l'information
Trois musiciens sont sur une scène. Chacun d'eux porte un costume de couleur différente : un cyan (C), un jaune (J) et un vert (V). Ils sont éclairés par trois spots lumineux indépendants, chacun étant d'une couleur primaire différente.
1.
Comment apparaissent-ils en lumière blanche ?
2. Comment faire disparaître uniquement V ? De quelle couleur apparaissent les deux autres musiciens ?
3. Est-il possible de faire disparaître J sans faire disparaître C ? Comment ?
4. Est-il possible de faire disparaître les trois musiciens ensemble ? Proposer deux solutions.
2. Comment faire disparaître uniquement V ? De quelle couleur apparaissent les deux autres musiciens ?
3. Est-il possible de faire disparaître J sans faire disparaître C ? Comment ?
4. Est-il possible de faire disparaître les trois musiciens ensemble ? Proposer deux solutions.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31Copie d'élève à commenter
Proposer une justification pour chaque erreur relevée par le correcteur.
1.
Une lentille est convergente si elle a un foyer à droite d'elle.
2. Comme la distance focale de cette lentille convergente est de 20 cm on a \color{red}\xcancel{\color{black}{\text{OF}^{\prime}=10}} cm.
3. On sait que \overline{\text{OA}}=-40 cm et \overline{\text{OF}}^{\prime}=20 cm.
On utilise la relation de conjugaison des lentilles convergentes :
On isole le terme recherché :
2. Comme la distance focale de cette lentille convergente est de 20 cm on a \color{red}\xcancel{\color{black}{\text{OF}^{\prime}=10}} cm.
3. On sait que \overline{\text{OA}}=-40 cm et \overline{\text{OF}}^{\prime}=20 cm.
On utilise la relation de conjugaison des lentilles convergentes :
\color{red}\xcancel{\color{black}{\dfrac{1}{\overline{\text{OA}^{\prime}}}+\dfrac{1}{\overline{\text{OA}}}=\dfrac{1}{\overline{\text{OF}^{\prime}}}}}
On isole le terme recherché :
\color{red}\cancel{\color{black}{\dfrac{1}{\overline{\text{OA}^{\prime}}}=\dfrac{1}{\overline{\text{OF}^{\prime}}}-\dfrac{1}{\overline{\text{OA}}}}}
\color{red}\cancel{\color{black}{\dfrac{1}{\overline{\text{OA}^{\prime}}}=\dfrac{1}{20}-\dfrac{1}{40}}}
\color{red}\cancel{\color{black}{\dfrac{1}{\overline{\text{OA}^{\prime}}}=\dfrac{1}{40}}}
\color{red}\cancel{\color{black}{\overline{\text{OA}^{\prime}}=40}} cm
\color{red}\cancel{\color{black}{\dfrac{1}{\overline{\text{OA}^{\prime}}}=\dfrac{1}{20}-\dfrac{1}{40}}}
\color{red}\cancel{\color{black}{\dfrac{1}{\overline{\text{OA}^{\prime}}}=\dfrac{1}{40}}}
\color{red}\cancel{\color{black}{\overline{\text{OA}^{\prime}}=40}} cm
4.
La relation de grandissement est \color{red}\xcancel{\color{black}{\gamma=\dfrac{\text{OA}^{\prime}}{\text{OA}}}}.
On trouve \color{red}\xcancel{\color{black}{\gamma = 1}} donc l'image est de la même taille que l'objet etdroite.
5. L'image est de couleur blanche. Elle est donc le résultat dumélange de lumières rouge, verte et bleue.
6. Pour voir cette image de couleur cyan, il faut l'éclairer avec une lumièrecyan.
7. Pour voir cette image noire, il faut l'éclairer avec une lumièrenoire.
On trouve \color{red}\xcancel{\color{black}{\gamma = 1}} donc l'image est de la même taille que l'objet et
5. L'image est de couleur blanche. Elle est donc le résultat du
6. Pour voir cette image de couleur cyan, il faut l'éclairer avec une lumière
7. Pour voir cette image noire, il faut l'éclairer avec une lumière
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32Vision en trichromie et feu rouge
✔ RAI/ANA : Choisir un protocoleUn conducteur de voiture arrive à un feu tricolore. Il s'arrête car le feu est rouge. Son ami côté passager est daltonien. Le tableau ci-dessous présente des exemples de vision de couleurs de la personne daltonienne.
|
Couleur perçue par un œil normal |
Couleur perçue par le daltonien |
|
Jaune |
Vert |
|
Magenta |
Bleu |
1. Déterminer quel est le cône qui ne fonctionne pas chez cette personne daltonienne.
2. Une personne daltonienne doit-elle retenir la couleur des feux ou la position des lumières pour bien s'arrêter ?
3. Si les trois feux (rouge, vert et orange) sont perçus éteints par la personne daltonienne, que doit-elle faire ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AUn indicateur de pH : le BBT
✔ APP : Extraire l'information utile sur supports variés
Le bleu de bromothymol (BBT) est une molécule qui change de couleur selon le pH de la solution dans laquelle elle se trouve. Le spectre d'absorption du BBT pour 3 types de solutions est donné dans le doc. 2.
Le bleu de bromothymol (BBT) est une molécule qui change de couleur selon le pH de la solution dans laquelle elle se trouve. Le spectre d'absorption du BBT pour 3 types de solutions est donné dans le doc. 2.
Doc. 1
Correspondance entre couleurs et longueur d'onde
Doc. 2
Spectre d'absorbance du BBT pour différents pH
1. Parmi les couleurs du doc. 1, identifier les couleurs primaires de la synthèse additive et celles de la synthèse soustractive.
2. Expliquer pourquoi le magenta est associé à « ~380-420 nm + ~700-780 nm ».
3. De quelle couleur est le BBT pour les 3 types de solutions ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BVision et hypermétropie
On modélise un œil par une lentille mince convergente et un écran. Lorsque cet œil est au repos, sa vergence est en moyenne \text{V}_{\text{repos}} = 60{,}0 δ. Le punctum proximum est la distance la plus petite où l'on parvient à voir un objet net en accommodant au maximum, la vergence de l'œil est alors en moyenne \text{V}_{\text{pp}} = 62{,}8 δ. La distance lentille‑écran est, pour un œil normal, de 16,7 mm en moyenne. Un œil hypermétrope est trop court, on supposera pour les calculs que la distance lentille‑écran de l'œil hypermétrope est de 16,0 mm.
Doc. 1
Vergence
La vergence d'une lentille est l'inverse de sa distance focale : \text{V} = 1 / \text{f}^{\prime}.
Elle s'exprime en général en dioptrie (δ), unité définie par : 1 δ = 1 m-1.
Elle s'exprime en général en dioptrie (δ), unité définie par : 1 δ = 1 m-1.
Doc. 2
Image d'un objet situé à l'infini
Lorsqu'un objet est situé très loin de la lentille (on modélise cette situation par une distance \text{AO} infinie), l'image se forme à une distance égale à la distance focale : \text{OA}^{\prime} = \text{f}^{\prime}.
1. Punctum proximum de l'œil normal
a. Calculer le punctum proximum de l'œil normal.
b. Un observateur avec un œil normal regarde un objet \text{AB} de taille 5{,}0 cm situé à son punctum proximum. Calculer la taille de l'image qui se forme sur la rétine.
2. Œil normal au repos
a. Calculer la distance focale de l'œil normal au repos.
b. Où doit se situer un objet pour qu'un œil normal le voit net au repos ?
3. Œil hypermétrope
a. Quelle devrait être la vergence de l'œil hypermétrope pour voir net un objet situé à l'infini ?
b. Pourquoi une personne hypermétrope ressent‑elle une fatigue visuelle en fin de journée ?
a. Calculer le punctum proximum de l'œil normal.
b. Un observateur avec un œil normal regarde un objet \text{AB} de taille 5{,}0 cm situé à son punctum proximum. Calculer la taille de l'image qui se forme sur la rétine.
2. Œil normal au repos
a. Calculer la distance focale de l'œil normal au repos.
b. Où doit se situer un objet pour qu'un œil normal le voit net au repos ?
3. Œil hypermétrope
a. Quelle devrait être la vergence de l'œil hypermétrope pour voir net un objet situé à l'infini ?
b. Pourquoi une personne hypermétrope ressent‑elle une fatigue visuelle en fin de journée ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
