Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilit és
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 1
Avant de commencer
Suites numériques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Calculer les termes d'une suite.
2. Déterminer le sens de variation d'une suite.
3. Représenter graphiquement une suite.
2. Déterminer le sens de variation d'une suite.
3. Représenter graphiquement une suite.
4. Reconnaître une suite arithmétique.
5. Reconnaître une suite géométrique.
6. Utiliser un algorithme pour calculer les termes d'une suite.
5. Reconnaître une suite géométrique.
6. Utiliser un algorithme pour calculer les termes d'une suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Les suites numériques sont présentes dans de nombreux domaines relevant de la modélisation. Parmi ces suites, l'une des plus connues est la suite de Fibonacci définie par :
Historiquement, elle proviendrait du mathématicien italien Fibonacci qui aurait souhaité étudier l'évolution d'une population de lapins. Aujourd'hui, cette suite apparaît dans la réalisation de nombreuses œuvres d'art.
\left\{\begin{array}{c}
u_{n+2}=u_{n+1}+u_{n} \\
u_{0}=1 \;; u_{1}=1
\end{array}\right.
Historiquement, elle proviendrait du mathématicien italien Fibonacci qui aurait souhaité étudier l'évolution d'une population de lapins. Aujourd'hui, cette suite apparaît dans la réalisation de nombreuses œuvres d'art.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Rappels théoriques
Supplément numérique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Développer et factoriser des expressions algébriques :
Développer une expression : transformer un produit en somme.
Soient k , a , b , c et d des nombres quelconques. On a les propriétés suivantes :1. Distributivité simple : k(a+b) = ka+kb
2. Double distributivité : (a+b)(c+d) = ac+ad+bc+bd
3. Identité remarquable : (a+b)(a-b) = a^2-b^2
Factoriser une expression : transformer une somme en produit.
1. Avec un facteur commun : ka + kb = k(a+b) ou ka - kb = k(a-b)2. Identités remarquables :
a^2 -b^2 = (a+b)(a-b)
a^2 + 2ab + b^2 = (a+b)^2
a^2 - 2ab +b^2 = (a-b)^2
a^2 + 2ab + b^2 = (a+b)^2
a^2 - 2ab +b^2 = (a-b)^2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calculer l'image d'un nombre par une fonction :
Méthode :
Si une fonction est donnée par une formule, on calcule l'image d'un nombre en remplaçant x par ce nombre dans la formule.Exemple :
Pour calculer l'image de 3 par f : x \mapsto 2x^2 +6x+3 , on calcule f(3) = 2\times 3^2 + 6 \times 3 + 3 = 39 .Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Étudier le signe d'une fonction :
Méthode :
Pour étudier le signe d'une fonction, on essaie de factoriser au maximum, puis on étudie le signe de chacun des facteurs en résolvant des inéquations et on regroupe les résultats dans un tableau de signes.Exemple :
Soit f : x \mapsto (x+1)(4x+2) - (x+1)(2x-4) définie sur \mathbb R . En utilisant la distributivité, on factorise f(x) = (x+1)(4x + 2 - (2x-4)) = (x+1)(2x +6) .On résout les inéquations x+ 1 \leqslant 0 \Leftrightarrow x \leqslant -1 et 2x + 6 \leqslant 0 \Leftrightarrow 2x \leqslant -6 \Leftrightarrow x \leqslant \dfrac{-6}{2} = -3 .
Le zoom est accessible dans la version Premium.
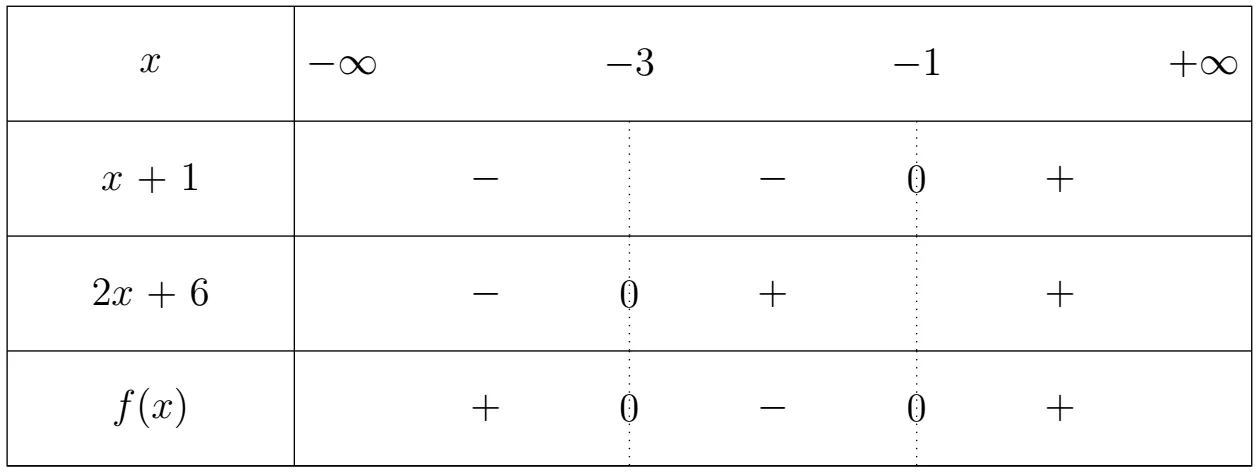
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Placer des points dans un repère :
Définition :
Dans un repère orthonormé (\text{O} \; ; \text{I}, \text{J}) :- \text{O} est l'origine du repère ;
- la droite (\text{OI}) (horizontale) est l'axe des abscisses ;
- la droite (\text{OJ}) (verticale) est l'axe des ordonnées.
Un point \text{M} du plan est repéré par ses coordonnées x (abscisse, obtenue en projetant \text{M} sur l'axe des abscisses) et y (ordonnée, obtenue en projetant \text{M} sur l'axe des ordonnées).
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calculer des pourcentages :
Définition :
Un pourcentage est une proportion exprimée sous la forme d'une fraction dont le dénominateur est 100.Propriétés :
1. Augmenter un nombre de p % revient à multiplier ce nombre par 1 + \dfrac{p}{100} .2. Diminuer un nombre de p % revient à multiplier ce nombre par 1 - \dfrac{p}{100} .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Développer et factoriser des expressions algébriques.
2. Calculer l'image d'un nombre par une fonction.
3. Étudier le signe d'une fonction.
4. Placer des points dans un repère.
5. Calculer des pourcentages.
2. Calculer l'image d'un nombre par une fonction.
3. Étudier le signe d'une fonction.
4. Placer des points dans un repère.
5. Calculer des pourcentages.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1Développement
Soit n un entier naturel.
Développer les expressions algébriques suivantes.
1. 2 \times(2 n+3)
2. (n+1)(n-2)
3. (2 n+5)^{2}
4. (4-n)^{2}
Développer les expressions algébriques suivantes.
1. 2 \times(2 n+3)
2. (n+1)(n-2)
3. (2 n+5)^{2}
4. (4-n)^{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 2Factorisation
Soit n un entier naturel.
Factoriser les expressions suivantes.
1. 3 n-6
2. n^{2}+2 n
3. 4 n^{2}+20 n+25
4. n^{2}-2 n+1
Factoriser les expressions suivantes.
1. 3 n-6
2. n^{2}+2 n
3. 4 n^{2}+20 n+25
4. n^{2}-2 n+1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 3Image d'un nombre par une fonction (1)
Soient f et g les fonctions définies sur \R par :
Calculer les images de 0, 1, 2, 5 et 10 par chacune de ces fonctions.
f(x)=3 x+2 et g(x)=2 x^{2}+3 x-4.
Calculer les images de 0, 1, 2, 5 et 10 par chacune de ces fonctions.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 4Image d'un nombre par une fonction (2)
Soient h et k les fonctions définies sur \R par :
Pour tout entier naturel n, calculer et simplifier au maximum les images de n, 2n, n + 1 et n - 2 par ces fonctions.
h(x)=x^{2}-2 et k(x)=(x-3)^{2}+1.
Pour tout entier naturel n, calculer et simplifier au maximum les images de n, 2n, n + 1 et n - 2 par ces fonctions.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 5Coordonnées d'un point
Dans un repère orthonormé (\mathrm{O} \; ; \mathrm{I}\,, \mathrm{J}) du plan, placer les points de coordonnées :
\mathrm{A}(0 \; ; 1), \mathrm{B}\left(1 \; ; \dfrac{1}{2}\right), \mathrm{C}(2 \;;-1), \mathrm{D}\left(3 \; ; \dfrac{5}{2}\right) et \mathrm{E}(4 \; ; 4)
\mathrm{A}(0 \; ; 1), \mathrm{B}\left(1 \; ; \dfrac{1}{2}\right), \mathrm{C}(2 \;;-1), \mathrm{D}\left(3 \; ; \dfrac{5}{2}\right) et \mathrm{E}(4 \; ; 4)
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 6Tableur
On considère la feuille de calcul suivante.
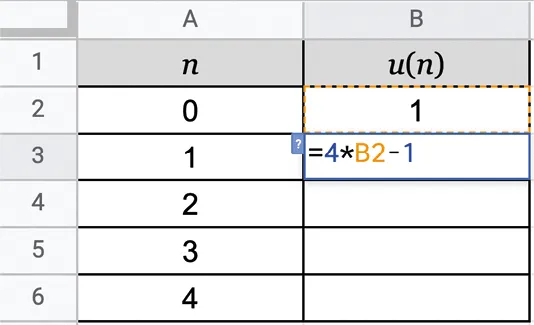
1. Quelle sera la valeur obtenue dans la cellule B3 ?
2. En étirant la formule de la cellule B3 vers le bas, quelle formule apparaîtra dans la cellule B6 ?
Quelle sera la valeur affichée ?
Le zoom est accessible dans la version Premium.
1. Quelle sera la valeur obtenue dans la cellule B3 ?
2. En étirant la formule de la cellule B3 vers le bas, quelle formule apparaîtra dans la cellule B6 ?
Quelle sera la valeur affichée ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 7Évolution en pourcentage
Compléter les phrases suivantes.
1. Augmenter une quantité de 8 % revient à la multiplier par.
2. Diminuer une quantité de 15 % revient à la multiplier par.
1. Augmenter une quantité de 8 % revient à la multiplier par
2. Diminuer une quantité de 15 % revient à la multiplier par
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 8Problème
En 2018, la production de chocolat en France s'élevait à 333 \; 029 tonnes. Elle a augmenté de 5 % en 2019 et on estime qu'en 2020, elle augmentera encore de 7 %.
1. Quelle quantité de chocolat a été produite en 2019 ?
2. Calculer la quantité de chocolat produite prévue en 2020.
3. Du fait de la crise sanitaire, la production de chocolat a diminué de 11 % entre 2019 et 2020, mais les prévisions indiquent qu'elle augmentera de 6 % en 2021.
Quelle sera la quantité produite en 2020 et en 2021 ?
1. Quelle quantité de chocolat a été produite en 2019 ?
2. Calculer la quantité de chocolat produite prévue en 2020.
3. Du fait de la crise sanitaire, la production de chocolat a diminué de 11 % entre 2019 et 2020, mais les prévisions indiquent qu'elle augmentera de 6 % en 2021.
Quelle sera la quantité produite en 2020 et en 2021 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Il est possible de calculer la somme des n premiers entiers, c'est‑à‑dire la valeur de 1+2+3+4+\ldots +n, avec la formule \dfrac{n(n+1)}{2}.
Cette formule est au programme de la classe de Terminale.
Le nombre \dfrac{n(n+1)}{2} obtenu correspond par exemple :
Cette formule est au programme de la classe de Terminale.
Le nombre \dfrac{n(n+1)}{2} obtenu correspond par exemple :
- au nombre de segments que l'on peut tracer entre n + 1 points distincts ;
- au nombre de poignées de mains échangées dans un rassemblement de n + 1 personnes (en supposant que chaque personne serre la main à une autre exactement une fois).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah