Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 1
Exercices
Synthèse
10 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 102 [Raisonner, Modéliser.]
D'après bac STI2D, Métropole, 2019
1. Que vaut u_0 ? Montrer que u_{1}=84{,}5
2. Justifier que, pour tout entier naturel n, on a :
u_{n+1}=1{,}05 u_{n}-10
3. Donner une valeur arrondie de u_2 et u_3 à 10^{-3} près.
4. La suite \left(u_{n}\right) est-elle arithmétique ? Géométrique ?
5. Ce plan d'éradication prendra fin quand l'aire occupée sera inférieure à 6 hectares. Compléter l'algorithme ci-dessous pour que la variable n contienne le nombre d'années que durera le plan, puis déterminer en quelle année ce plan prendra fin.
Le conservatoire des espaces naturels d'une région gère une zone protégée de 1\,800 hectares.
Il a remarqué qu'une plante invasive occupait un espace dont la surface augmente de 5 % chaque année. Le conservatoire constate qu'à la fin de l'année 2020, l'aire de la surface occupée par cette plante est de 90 hectares et décide d'éliminer 10 hectares occupés par cette plante par an à partir de 2021. Pour tout entier naturel n, on note u_n l'aire de la surface occupée par cette plante en 2020 + n.
Il a remarqué qu'une plante invasive occupait un espace dont la surface augmente de 5 % chaque année. Le conservatoire constate qu'à la fin de l'année 2020, l'aire de la surface occupée par cette plante est de 90 hectares et décide d'éliminer 10 hectares occupés par cette plante par an à partir de 2021. Pour tout entier naturel n, on note u_n l'aire de la surface occupée par cette plante en 2020 + n.
Le zoom est accessible dans la version Premium.
\boxed{
\begin{array} { r|l } 1 & n \leftarrow 0 \\
2 & \text{U} \leftarrow 90 \\
3 & \text { Tant que U} \geqslant 6 \\
4 & \quad \text {U} \leftarrow \text { ... } \\
5 & \quad n \leftarrow \text { ... } \\
6 & \text{Fin tant que}
\end{array}
}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 103 [Calculer, représenter.]
On considère une suite \left(u_{n}\right) vérifiant, pour tout entier naturel n, la relation de récurrence : u_{n+2}=2 u_{n+1}-u_{n}
1. La connaissance du premier terme u_0 est-elle suffisante pour calculer les autres termes ?
On choisit u_{0}=0 et u_{1}=1 pour la suite de l'exercice.
2. a. Calculer les sept premiers termes de la suite \left(u_{n}\right) et représenter ces termes sur un graphique.
1. La connaissance du premier terme u_0 est-elle suffisante pour calculer les autres termes ?
On choisit u_{0}=0 et u_{1}=1 pour la suite de l'exercice.
2. a. Calculer les sept premiers termes de la suite \left(u_{n}\right) et représenter ces termes sur un graphique.
2. b. Conjecturer le sens de variation de u_n. On admettra que
cette conjecture est vraie pour la suite.
2. c. Justifier alors que, pour tout entier naturel n, u_n est positif.
2. c. Justifier alors que, pour tout entier naturel n, u_n est positif.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 104 [Modéliser, Raisonner.]
D'après bac ES, Métropole, 2019
En 2018, Laurence a acheté une ferme de 14 hectares de pommiers. Elle estime qu'il y a 300 pommiers par hectare. Chaque année, elle élimine 8 % des pommiers et replante 38 nouveaux pommiers par hectare.
Pour tout entier naturel n, on note u_n le nombre de pommiers par hectare l'année 2018 + n. Ainsi, u_{0}=300.
1. a. Justifier que, pour tout entier naturel n, on a u_{n+1}=0{,}92 u_{n}+38.
1. b. Estimer le nombre de pommiers par hectare, arrondi à l'unité, en 2020.
2. Laurence veut savoir à partir de quelle année la densité de pommiers, par hectare, dépassera 400. Elle utilise alors l'algorithme ci-dessous :
a. Compléter l'algorithme pour qu'il détermine le rang cherché.
b. Quelle est la valeur contenue dans la variable \text{N} en sortie de l'algorithme ?
Pour tout entier naturel n, on note u_n le nombre de pommiers par hectare l'année 2018 + n. Ainsi, u_{0}=300.
1. a. Justifier que, pour tout entier naturel n, on a u_{n+1}=0{,}92 u_{n}+38.
1. b. Estimer le nombre de pommiers par hectare, arrondi à l'unité, en 2020.
2. Laurence veut savoir à partir de quelle année la densité de pommiers, par hectare, dépassera 400. Elle utilise alors l'algorithme ci-dessous :
\boxed{
\begin{array} { r|l } 1 & \text{N} \leftarrow 0 \\
2 & \text{U} \leftarrow 300 \\
3 & \text { Tant que U} \text { ... } \\
4 & \quad \text {N} \leftarrow \text { N}+1 \\
5 & \quad \text{U} \leftarrow \text { ... } \\
6 & \text{Fin tant que}
\end{array}
}
a. Compléter l'algorithme pour qu'il détermine le rang cherché.
b. Quelle est la valeur contenue dans la variable \text{N} en sortie de l'algorithme ?
3. On définit la suite \left(v_{n}\right) en posant, pour tout entier
naturel n, v_{n}=u_{n}-475.
a. On admet que \left(v_{n}\right) est une suite géométrique de raison 0{,}92. Préciser son premier terme et déterminer une relation de récurrence vérifiée par la suite \left(v_{n}\right).
b. En admettant que v_{n}=-175 \times 0{,}92^{n}, exprimer u_n en fonction de n.
c. Combien devrait-on compter de pommiers dans l'exploitation de Laurence en 2027 ?
a. On admet que \left(v_{n}\right) est une suite géométrique de raison 0{,}92. Préciser son premier terme et déterminer une relation de récurrence vérifiée par la suite \left(v_{n}\right).
b. En admettant que v_{n}=-175 \times 0{,}92^{n}, exprimer u_n en fonction de n.
c. Combien devrait-on compter de pommiers dans l'exploitation de Laurence en 2027 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 105 [Modéliser, Calculer.]
D'après bac ST2S, Antilles, 2018
Lors d'une scintigraphie cardiaque, on injecte au patient un échantillon d'un isotope de thallium d'activité radioactive 120 \text{MBq} (Mégabecquerel).
À chaque demi-vie, le thallium perd la moitié de son activité. On sait que la demi-vie du thallium est de 3 jours. Pour tout entier naturel n, on note \mathrm{A}_{n} l'activité de l'échantillon après n demi-vies.
1. Donner les valeurs de \mathrm{A}_{0}, \mathrm{A}_{1}, \mathrm{A}_{2} et \mathrm{A}_{3}.
2. Exprimer \mathrm{A}_{n+1} en fonction de \mathrm{A}_{n}. En déduire la nature de la suite et sa raison.
À chaque demi-vie, le thallium perd la moitié de son activité. On sait que la demi-vie du thallium est de 3 jours. Pour tout entier naturel n, on note \mathrm{A}_{n} l'activité de l'échantillon après n demi-vies.
1. Donner les valeurs de \mathrm{A}_{0}, \mathrm{A}_{1}, \mathrm{A}_{2} et \mathrm{A}_{3}.
2. Exprimer \mathrm{A}_{n+1} en fonction de \mathrm{A}_{n}. En déduire la nature de la suite et sa raison.
3. Justifier que la suite \left(\mathrm{A}_{n}\right) est bien décroissante.
4. À l'aide de la calculatrice, trouver le nombre de jours au bout desquels l'activité radioactive devient inférieure à 0{,}25 \text{MBq}.
4. À l'aide de la calculatrice, trouver le nombre de jours au bout desquels l'activité radioactive devient inférieure à 0{,}25 \text{MBq}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 106 Tableur [Modéliser, Calculer.]
Pour étudier la propagation de bactéries dans des cellules, un laboratoire fait l'expérience suivante : on met en contact deux cellules, une première, notée A, avec 1\,000 bactéries au départ, et une seconde, notée B, sans bactérie. On constate que les bactéries migrent d'une cellule à l'autre, et qu'à chaque minute, 42 % des bactéries de la cellule A migrent vers la cellule B, et 23 % des bactéries de la cellule B migrent vers la cellule A.
On note \mathrm{A}_{n} le nombre de bactéries dans la cellule A et \mathrm{B}_{n} le nombre de bactéries dans la cellule B au bout de n minutes.
1. Que valent \mathrm{A}_{0} et \mathrm{B}_{0} ?
2. Justifier que pour tout entier naturel n :
On note \mathrm{A}_{n} le nombre de bactéries dans la cellule A et \mathrm{B}_{n} le nombre de bactéries dans la cellule B au bout de n minutes.
1. Que valent \mathrm{A}_{0} et \mathrm{B}_{0} ?
2. Justifier que pour tout entier naturel n :
\left\{\begin{aligned}
\mathrm{A}_{n+1}&=0{,}58 \mathrm{~A}_{n}+0{,}23 \mathrm{~B}_{n} \\
\mathrm{B}_{n+1}&=0{,}42 \mathrm{~A}_{n}+0{,}77 \mathrm{~B}_{n}
\end{aligned}\right.
3. Dans la feuille de calcul ci-dessous, quelles formules ont été entrées dans les cellules B3 et C3 pour obtenir les termes des suites \left(\mathrm{A}_{n}\right) et \left(\mathrm{B}_{n}\right) en étirant les formules vers le bas ?
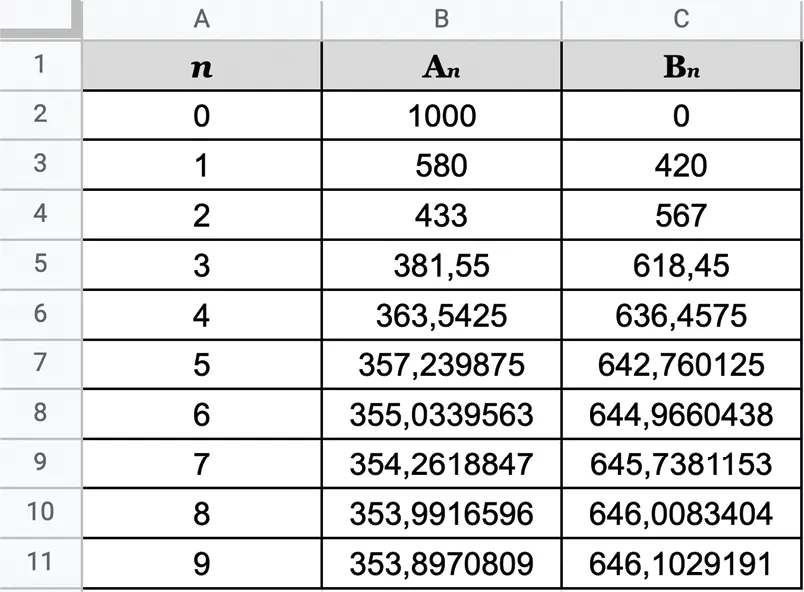
4. Conjecturer le sens de variation de \left(\mathrm{A}_{n}\right) et \left(\mathrm{B}_{n}\right).
Le zoom est accessible dans la version Premium.
4. Conjecturer le sens de variation de \left(\mathrm{A}_{n}\right) et \left(\mathrm{B}_{n}\right).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 107 [Chercher, Calculer.]
Dans le cours, nous avons défini les suites arithmétiques par une relation de récurrence. L'objectif de cet exercice est de déterminer une expression du terme général des suites arithmétiques.
Soit \left(u_{n}\right) une suite arithmétique de raison r définie pour tout entier naturel n.
1. Rappeler la relation de récurrence qui lie u_{n+1}, u_{n} et r.
2. Exprimer alors u_{1} en fonction de u_{0} et r.
3. Exprimer u_{2} en fonction de u_{1} et r, puis en fonction de u_{0} et r à l'aide de la question précédente.
1. Rappeler la relation de récurrence qui lie u_{n+1}, u_{n} et r.
2. Exprimer alors u_{1} en fonction de u_{0} et r.
3. Exprimer u_{2} en fonction de u_{1} et r, puis en fonction de u_{0} et r à l'aide de la question précédente.
4. Exprimer u_{3} en fonction de u_{2} et r, puis en fonction de u_{0} et r à l'aide de la question précédente.
5. Conjecturer alors une expression du terme général de la suite, c'est-à-dire exprimer u_n en fonction de n.
On admettra dans la suite que cette conjecture est vraie.
6. Soit \left(u_{n}\right) la suite arithmétique de raison 3 et de premier terme u_{0}=-8. Calculer la valeur de u_{100}.
5. Conjecturer alors une expression du terme général de la suite, c'est-à-dire exprimer u_n en fonction de n.
On admettra dans la suite que cette conjecture est vraie.
6. Soit \left(u_{n}\right) la suite arithmétique de raison 3 et de premier terme u_{0}=-8. Calculer la valeur de u_{100}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 108QCM [Raisonner, Calculer.]
D'après bac STMG, Polynésie, 2019
1. Soit \left(\mathrm{V}_{n}\right) la suite géométrique de raison q = 1{,}2 et de premier terme \mathrm{V}_{1}=6.
Quelle est la valeur, arrondie au dixième, de \mathrm{V}_{6} ?
2. Quelle est la valeur contenue dans n à la fin de cet algorithme ?
Quelle est la valeur, arrondie au dixième, de \mathrm{V}_{6} ?
2. Quelle est la valeur contenue dans n à la fin de cet algorithme ?
\boxed{
\begin{array} { r|l } 1 & n \leftarrow 1 \\
2 & \text{V} \leftarrow 6 \\
3 & \text { Tant que V} \lt 31 \\
4 & \quad n \leftarrow n+1 \\
5 & \quad \text{V} \leftarrow \text {V}\times 1{,}2 \\
6 & \text{Fin tant que}
\end{array}
}
3. Soit \left(\mathrm{U}_{n}\right) la suite arithmétique de raison 3 et telle que \mathrm{U}_{4}=81. Alors \mathrm{U}_{0} est égal à :
4. La suite \left(\mathrm{W}_{n}\right) vérifiant, pour tout entier naturel n, \mathrm{W}_{n+1}=\mathrm{W}_{n}+n^{2}-2 n+1 est :
4. La suite \left(\mathrm{W}_{n}\right) vérifiant, pour tout entier naturel n, \mathrm{W}_{n+1}=\mathrm{W}_{n}+n^{2}-2 n+1 est :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 109 Geogebra [Représenter, Calculer.]
On définit, pour tout entier naturel n, les suites \left(u_{n}\right) et \left(v_{n}\right)
par u_{n}=n^{2}-\frac{5}{2} n-1 et v_{n}=2 n^{2}-6 n-1.
1. Calculer les quatre premiers termes de ces deux suites.
2. Représenter sur GeoGebra les dix premiers termes de ces deux suites.
1. Calculer les quatre premiers termes de ces deux suites.
2. Représenter sur GeoGebra les dix premiers termes de ces deux suites.
GeoGebra
3. Déterminer graphiquement à partir de quel rang n l'inégalité v_{n}>u_{n} est vérifiée.
4. Montrer que, pour tout entier naturel n, on a :
5. Démontrer alors le résultat obtenu à la question 3.
4. Montrer que, pour tout entier naturel n, on a :
v_{n}-u_{n}=n \times\left(n-\frac{7}{2}\right).
5. Démontrer alors le résultat obtenu à la question 3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 110 VRAI/FAUX [Chercher, Raisonner.]
On considère un polygone régulier à n côtés de longueur égale à 1+\frac{1}{n}.
Pour tout entier naturel n supérieur ou égal à 3, on note u_n le périmètre de ce polygone.
Ainsi, u_3 est le périmètre d'un triangle équilatéral de côté 1+\frac{1}{3}=\frac{4}{3}.
Déterminer, en justifiant, si les affirmations suivantes sont vraies ou fausses.
1. On a u_{3}=\frac{4}{3}
2. La suite \left(u_{n}\right) est telle que, pour tout entier naturel n supérieur ou égal à 3, u_{n}=n \times\left(1+\frac{1}{n}\right)+1.
Pour tout entier naturel n supérieur ou égal à 3, on note u_n le périmètre de ce polygone.
Ainsi, u_3 est le périmètre d'un triangle équilatéral de côté 1+\frac{1}{3}=\frac{4}{3}.
Déterminer, en justifiant, si les affirmations suivantes sont vraies ou fausses.
1. On a u_{3}=\frac{4}{3}
3. La suite \left(u_{n}\right) est arithmétique de raison 1.
4. La suite \left(u_{n}\right) est croissante.
4. La suite \left(u_{n}\right) est croissante.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 111 [Chercher, Calculer.]
Dans le cours, nous avons défini les suites géométriques par une relation de récurrence. L'objectif de cet exercice est de déterminer une expression du terme général des suites géométriques.
Soit \left(v_{n}\right) une suite géométrique de raison q définie pour tout entier naturel n.
1. Rappeler la relation de récurrence qui lie v_{n+1}, v_{n} et q.
2. Exprimer alors v_1 en fonction de v_0 et q.
3. Exprimer v_2 en fonction de v_1 et q, puis en fonction de v_0 et q à l'aide de la question précédente.
Soit \left(v_{n}\right) une suite géométrique de raison q définie pour tout entier naturel n.
1. Rappeler la relation de récurrence qui lie v_{n+1}, v_{n} et q.
2. Exprimer alors v_1 en fonction de v_0 et q.
3. Exprimer v_2 en fonction de v_1 et q, puis en fonction de v_0 et q à l'aide de la question précédente.
4. Exprimer v_3 en fonction de v_2 et q, puis en fonction de v_0 et q à l'aide de la question précédente.
5. Conjecturer alors une expression du terme général de la suite \left(v_{n}\right), c'est-à-dire exprimer v_n en fonction de n et q.
On admettra dans la suite que cette conjecture est exacte.
6. Soit \left(v_{n}\right) la suite géométrique de raison 2 et de premier terme v_{0}=1{,}1. Calculer la valeur de v_{50}.
5. Conjecturer alors une expression du terme général de la suite \left(v_{n}\right), c'est-à-dire exprimer v_n en fonction de n et q.
On admettra dans la suite que cette conjecture est exacte.
6. Soit \left(v_{n}\right) la suite géométrique de raison 2 et de premier terme v_{0}=1{,}1. Calculer la valeur de v_{50}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 112 PYTHON [Calculer, Modéliser.]
La suite de Syracuse est une suite de nombres entiers définis de la manière suivante :
- on choisit un entier naturel non nul ;
- si ce nombre est pair, on le divise par 2 ; s'il est impair, on le multiplie par 3 et on ajoute 1 ;
- on recommence le procédé avec le nombre obtenu à l'étape précédente.
1. a. Déterminer les six premiers termes de la suite pour trois entiers choisis entre 1 et 5.
b. Que remarque-t-on ?
b. Que remarque-t-on ?
2.
a. Écrire un programme Python syracuse prenant en argument un entier u correspondant au premier terme de la suite et un entier n et renvoyant la liste des n premiers termes de la suite de Syracuse.
b. Tester le programme pour différentes valeurs de l'entier u.
Quelle conjecture peut-on formuler ?
Cette conjecture est appelée la conjecture de Syracuse.
Aide
L'instruction « Si u est pair » peut s'écrire if u%2 == 0.
b. Tester le programme pour différentes valeurs de l'entier u.
Quelle conjecture peut-on formuler ?
Cette conjecture est appelée la conjecture de Syracuse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La conjecture de Syracuse affirme qu'au bout d'un certain rang, les termes de la suite définie dans cet exercice formeront nécessairement la suite de nombre 1, 4, 2, 1, 4, 2, 1, 4, 2, etc., et cela quelle que soit la valeur du premier terme entier choisi.
Elle est énoncée en 1937 par le mathématicien allemand Lothar Collatz et est popularisée par son compatriote Helmut Hasse lors d'un voyage à l'université de Syracuse aux États-Unis. Elle a particulièrement mobilisé les mathématiciens durant la guerre froide.
Si l'énoncé de la conjecture est très simple, aucune démonstration de ce résultat n'existe à ce jour.
Elle est énoncée en 1937 par le mathématicien allemand Lothar Collatz et est popularisée par son compatriote Helmut Hasse lors d'un voyage à l'université de Syracuse aux États-Unis. Elle a particulièrement mobilisé les mathématiciens durant la guerre froide.
Si l'énoncé de la conjecture est très simple, aucune démonstration de ce résultat n'existe à ce jour.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Club de maths
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 113 CASSE TÊTE
On effectue le coloriage d'un carré de côté 2 de la manière suivante.
Étape 1 : On coupe le carré initial en quatre carrés identiques de côté c_1, et on colorie le carré en bas à gauche.
Étape 2 : Pour chacun des carrés non coloriés, on effectue à nouveau l'étape précédente et on continue ainsi.
On note k_n le nombre de carrés coloriés au cours de l'étape n, et c_n la longueur des côtés de ces carrés. D'où k_{1}=1 et k_{2}=3.
1. Faire le coloriage de l'étape 3.
2. Donner la valeur de k_3, puis déterminer l'expression de k_{n+1} en fonction de k_n.
3. Donner les valeurs de c_1, c_2 et c_3.
4. Justifier que, pour tout entier naturel n non nul, c_{n}=\left(\frac{1}{2}\right)^{n-1}
Étape 1 : On coupe le carré initial en quatre carrés identiques de côté c_1, et on colorie le carré en bas à gauche.
Étape 2 : Pour chacun des carrés non coloriés, on effectue à nouveau l'étape précédente et on continue ainsi.
On note k_n le nombre de carrés coloriés au cours de l'étape n, et c_n la longueur des côtés de ces carrés. D'où k_{1}=1 et k_{2}=3.
Le zoom est accessible dans la version Premium.
2. Donner la valeur de k_3, puis déterminer l'expression de k_{n+1} en fonction de k_n.
3. Donner les valeurs de c_1, c_2 et c_3.
4. Justifier que, pour tout entier naturel n non nul, c_{n}=\left(\frac{1}{2}\right)^{n-1}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 114 ÉNIGME
On souhaite construire des châteaux de cartes avec 10 paquets de 32 cartes. Le premier château doit être construit avec 2 cartes. Les autres châteaux doivent respecter la règle suivante : un château doit contenir deux fois plus de cartes que le précédent, plus une carte.
Combien de châteaux peut-on construire ?
Combien de châteaux peut-on construire ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 115 QUESTION OUVERTE
Un nouvel employé se voit proposer deux contrats différents, nommés A et B.
Le contrat A lui offre un salaire de 1\,500 € par mois avec une augmentation de 50 € par an.
Le contrat B lui offre un salaire de 1\,300 € par mois avec une augmentation de 5 % par an.
Quel contrat doit-il choisir sur le long terme ? Justifier.
Le contrat A lui offre un salaire de 1\,500 € par mois avec une augmentation de 50 € par an.
Le contrat B lui offre un salaire de 1\,300 € par mois avec une augmentation de 5 % par an.
Quel contrat doit-il choisir sur le long terme ? Justifier.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah