Chapitre 15
Problèmes et tâches complexes
Analyse spectrale des ondes lumineuses
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Constante de Wien : \sigma = 2,90 \times 10-3 m\cdotK ;
- Conversion de température : T_{(^{\circ} \text{C})}=T_{(\text{K})}- 273,15 ;
- Constante de Rydberg : R_{\mathrm{H}}= 1,10 \times 107 m-1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28 Loi empirique de Wien
✔ APP : Faire un brouillon

Wilhelm Wien (1864-1928), prix Nobel de physique en 1911, propose une loi liant la température d'un corps chaud et son émission de lumière :
\lambda_{\max } \cdot T=\sigma
Où \lambda_{\max } correspond à la longueur d'onde du maximum d'intensité lumineuse émise en mètre (m), T la température du corps chaud en kelvin (K) et \sigma la constante de Wien.
Le profil suivant correspond à l'évolution de l'intensité lumineuse émise par le Soleil en fonction de la longueur d'onde des radiations émises par celui-ci :

Déterminer la température en °C de la surface du Soleil.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29 Formule de Rydberg
✔ APP : Faire un brouillon

Johannes Rydberg propose en 1888 une formule permettant de déterminer la longueur d'onde de toutes les raies d'émission de l'atome d'hydrogène :
\dfrac{1}{\lambda}=R_{\mathrm{H}} \cdot\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right)
Dans cette formule, \lambda désigne la longueur d'onde en mètre de la raie considérée, R_{\mathrm{H}} une constante et n et p des entiers naturels non nuls tels que n \lt p. Ces deux entiers correspondent à des niveaux d'excitation possibles de l'atome d'hydrogène.

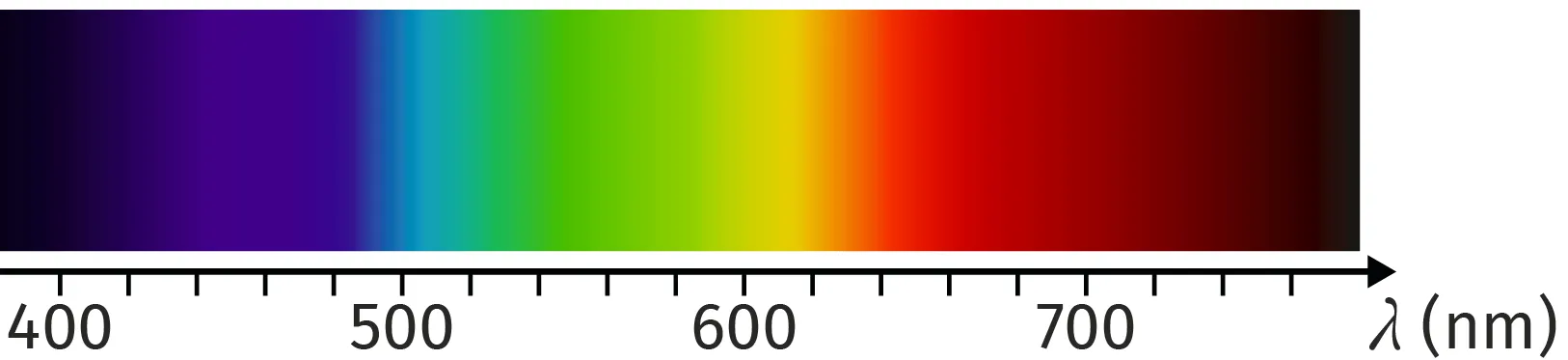
Spectre de la lumière
◆ À quelles couleurs sont associées les longueurs d'onde \lambda dans le spectre d'émission de l'hydrogène pour n= 2 et p \in [3, 6] ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retour sur la problématique du chapitre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
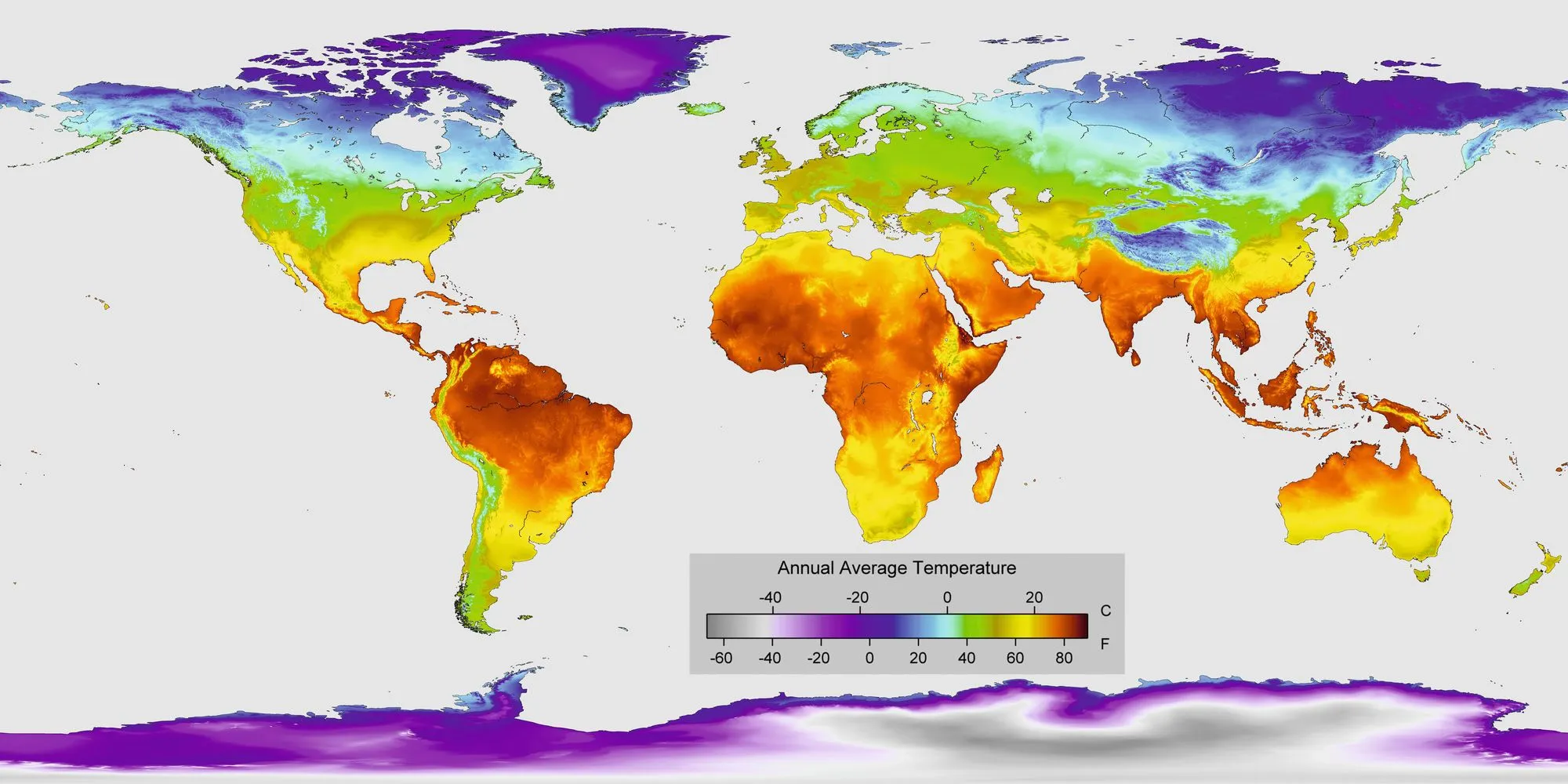
30 Les cartes météorologiques
✔ APP : Maîtriser le vocabulaire du cours
Expérimentalement, on remarque que la température de surface d'un corps chaud est inversement proportionnelle à la longueur d'onde du maximum d'intensité lumineuse émise.
Cette observation expérimentale justifie-t-elle l'ordre des couleurs utilisé dans la cartographie météorologique ci-contre ?
Cette observation expérimentale justifie-t-elle l'ordre des couleurs utilisé dans la cartographie météorologique ci-contre ?

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

