Chapitre 16
Cours
Propagation des ondes lumineuses
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Changement de milieu de propagation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
APhénomène de réflexion et de réfraction
La lumière se propage en ligne droite dans un milieu homogène et transparent. Cependant, lorsqu'elle change de milieu de propagation (passage de l'air à l'eau par exemple), la lumière peut subir deux phénomènes : une réflexion (le rayon repart dans le milieu initial) ou une réfraction (changement de direction de propagation). La surface de séparation entre deux milieux est appelée dioptre.
Le rayon arrivant sur le dioptre est appelé rayon incident, celui qui subit la réflexion est le rayon réfléchi et le rayon qui subit la réfraction est le rayon réfracté (doc. 1).
Le rayon arrivant sur le dioptre est appelé rayon incident, celui qui subit la réflexion est le rayon réfléchi et le rayon qui subit la réfraction est le rayon réfracté (doc. 1).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Notation des angles

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Attention à bien déterminer les angles entre le rayon et la normale et non pas entre le rayon et la surface de séparation !
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BLes lois du modèle de la réfraction et de la réflexion
On appelle angle d'incidence i_{1}, l'angle formé par le rayon incident et la normale au dioptre, angle de réfraction i_{2}, l'angle formé par le rayon réfracté et la normale au dioptre, et angle de réflexion r, l'angle formé par le rayon réfléchi et la normale.
Les lois de Snell-Descartes : elles ont été établies indépendamment par Willebrord Snell et René Descartes au XVIIe siècle.
Les lois de Snell-Descartes : elles ont été établies indépendamment par Willebrord Snell et René Descartes au XVIIe siècle.
- 1re loi de Snell-Descartes : le rayon incident, le rayon réfracté, le rayon réfléchi et la normale sont dans le même plan.
- 2e loi de Snell-Descartes :
n_{1} \cdot \sin \left(i_{1}\right)=n_{2} \cdot \sin \left(i_{2}\right) pour la réfraction ;
Et i_{1}= r pour la réflexion.
Remarque
Plus l'indice est grand, plus la vitesse de la lumière dans ce milieu est petite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Découvrez ici la présentation des lois de Snell‑Descartes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Indices de réfraction avec la vitesse de la lumière
| Milieu de propagation | Indice de réfraction | Vitesse de la lumière |
|---|---|---|
| Vide et air | 1,00 | 3,00 \times 108 m\cdots-1 |
| Eau | 1,33 | 2,25 \times 108 m\cdots-1 |
| Plexiglas | 1,49 | 2,01 \times 108 m\cdots-1 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 3Valeur d'indices pour l'eau en fonction de la longueur d'onde
| Longueur d'onde (nm) | Indice de réfraction |
|---|---|
| 400 (violet) | 1,343 |
| 580 (jaune) | 1,333 |
| 680 (rouge) | 1,332 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
C Dispersion de la lumière
La dispersion d'une lumière polychromatique (composée de plusieurs radiations donc de plusieurs couleurs) est le phénomène de séparation des radiations qui composent cette lumière.
On dit qu'un milieu est dispersif si son indice de réfraction dépend de la longueur d'onde de la radiation lumineuse qui le traverse.
Ce type de milieu permet de décomposer la lumière blanche.
L'image de cette décomposition des couleurs sur un écran s'appelle le spectre de la lumière.
Il peut permettre d'identifier si une source lumineuse est monochromatique ou non.
On dit qu'un milieu est dispersif si son indice de réfraction dépend de la longueur d'onde de la radiation lumineuse qui le traverse.
Ce type de milieu permet de décomposer la lumière blanche.
L'image de cette décomposition des couleurs sur un écran s'appelle le spectre de la lumière.
Il peut permettre d'identifier si une source lumineuse est monochromatique ou non.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 4Illustration de la dispersion de la lumière


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application : l'arc‑en‑ciel
L'arc‑en‑ciel est une application directe de la dispersion de la lumière du Soleil par les gouttes d'eau de la pluie qui tombent.
Chacune des gouttes agit comme un prisme et dévie les rayons lumineux différemment en fonction de leur longueur d'onde et donc de leur couleur.
La multiplicité des gouttes nous donne une vision d'ensemble de ce phénomène de dispersion qu'on appelle arc‑en‑ciel.
Chacune des gouttes agit comme un prisme et dévie les rayons lumineux différemment en fonction de leur longueur d'onde et donc de leur couleur.
La multiplicité des gouttes nous donne une vision d'ensemble de ce phénomène de dispersion qu'on appelle arc‑en‑ciel.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 5Dispersion dans une goutte d'eau

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Modélisation de l'œil par une lentille
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A La lentille mince convergente
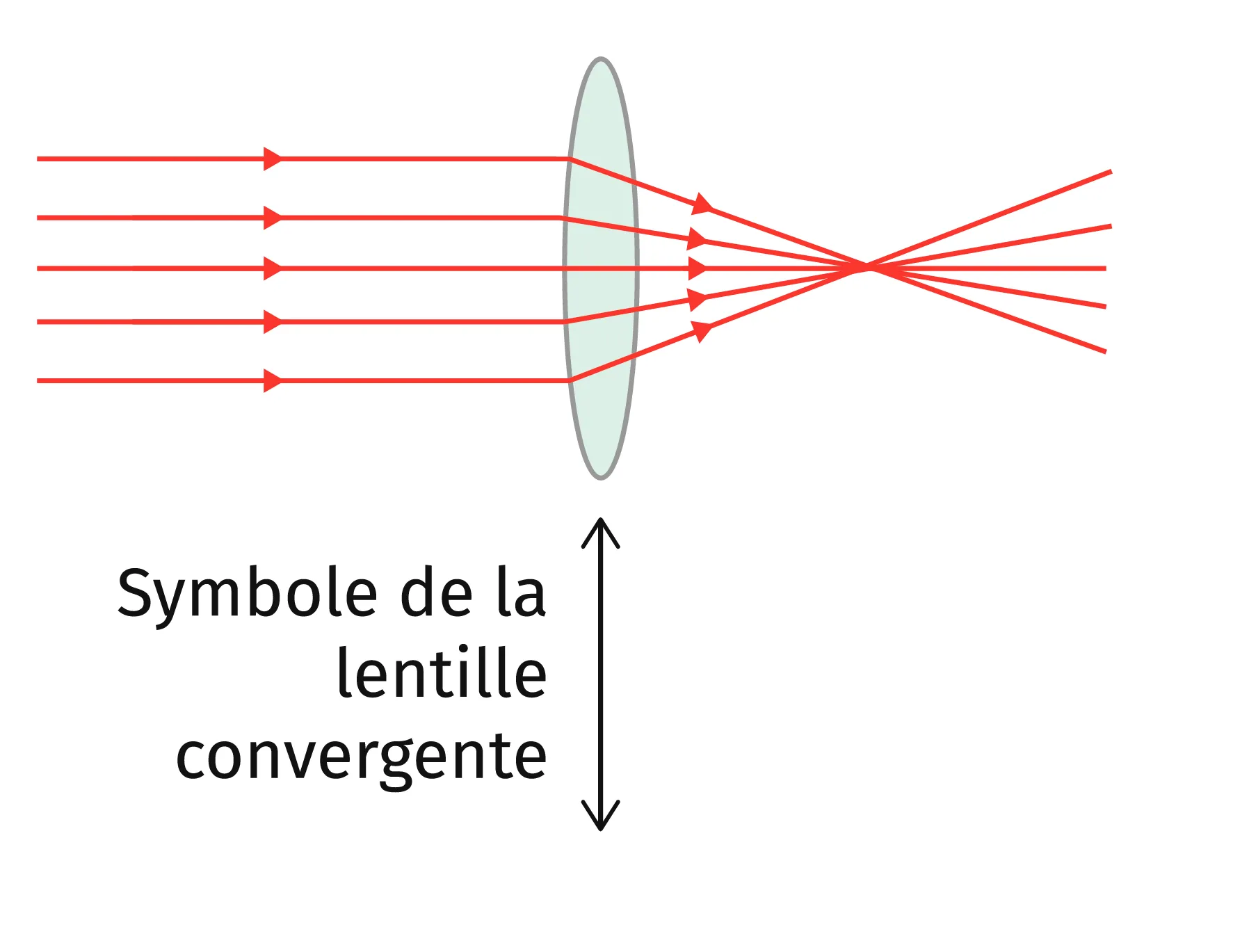
Une lentille mince convergente est un objet transparent de forme
circulaire dont l'épaisseur au centre est plus importante qu'au niveau de sa bordure. Ce système a la propriété de faire converger des rayons lumineux qui le traversent (voir doc. 6).
Une lentille mince convergente est caractérisée par son centre optique \mathrm{O} par lequel passe l'axe optique de la lentille \Delta, son foyer image \mathrm{F}^{\prime} et son foyer objet \mathrm{F} (\mathrm{F} est symétrique de \mathrm{F}^{\prime} par rapport à \mathrm{O}).
Une lentille mince convergente est caractérisée par son centre optique \mathrm{O} par lequel passe l'axe optique de la lentille \Delta, son foyer image \mathrm{F}^{\prime} et son foyer objet \mathrm{F} (\mathrm{F} est symétrique de \mathrm{F}^{\prime} par rapport à \mathrm{O}).
Remarque
On appelle distance focale f^{\prime} la distance entre \mathrm{O} et \mathrm{F}^{\prime}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Par convention, les rayons représentés vont toujours de gauche à droite. Pour une lentille convergente, attention à toujours placer le foyer image \mathrm{F}^{\prime} à droite et le foyer objet \mathrm{F} à gauche de \mathrm{O}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 6La lentille convergente

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Détermination graphique d'une image
Pour déterminer l'image d'un objet par une lentille convergente, il est pratique de tracer trois rayons particuliers issus d'un point \text{B} de cet objet, \text{B} étant situé hors de l'axe optique.
Ces rayons particuliers sont les suivants :
Après avoir traversé la lentille, ces rayons se croisent en un point \mathrm{B}^{\prime} qui est l'image de \mathrm{B} par la lentille.
Le grandissement \gamma est défini par le rapport entre la hauteur algébrique de l'image et celle de l'objet : \gamma=\dfrac{\overline{\mathbf{A}^{\prime} \mathbf{B}^{\prime}}}{\overline{\mathbf{A} \mathbf{B}}}.
Ces rayons particuliers sont les suivants :
- le rayon passant par le centre optique \mathrm{O} ne subit aucune déviation ;
- le rayon arrivant parallèlement à l'axe optique émerge de la lentille en passant par le foyer image \mathrm{F}^{\prime};
- le rayon passant par le foyer objet \mathrm{F} émerge parallèlement à l'axe optique.
Après avoir traversé la lentille, ces rayons se croisent en un point \mathrm{B}^{\prime} qui est l'image de \mathrm{B} par la lentille.
Le grandissement \gamma est défini par le rapport entre la hauteur algébrique de l'image et celle de l'objet : \gamma=\dfrac{\overline{\mathbf{A}^{\prime} \mathbf{B}^{\prime}}}{\overline{\mathbf{A} \mathbf{B}}}.
- Si \gamma\lt0 alors l'image est renversée par rapport à l'objet et si \gamma>0, on dit que l'image est droite.
- Si |\gamma|>1 alors l'image est agrandie par rapport à l'objet.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
C Modèle réduit de l'œil
L'œil est un système optique complexe mais qui peut se modéliser à l'aide de matériel simple de laboratoire (doc. 7).
➜ Voir l' p. 290
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Par convention, on considère un axe vertical orienté vers le haut sur les schémas. Ainsi, la hauteur algébrique d'un objet \overline{\mathrm{AB}} perpendiculaire à l'axe prend une valeur positive (\overline{\mathrm{AB}}>0) si cet objet est orienté vers le haut et négative (\overline{\mathrm{AB}}\lt0) s'il est orienté vers le bas. Il en est de même pour la hauteur \text { A'B' } de l'image \overline{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 7Modélisation de l'œil réduit

| Œil réel | Modèle réduit |
|---|---|
| Iris | Diaphragme |
| Cristallin | Lentille convergente |
| Rétine | Écran |
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

