L'Institut national de la Statistique et des Études économiques (INSEE) a publié une étude en 2015 qui montre que les salariés français gagnent en moyenne 2 250 € net par mois. Le salaire médian est de 1 797 € net par mois.
Note : Ces indicateurs sont calculés à partir des salaires en équivalents temps plein.

1. Comment l'INSEE a-t-il calculé cette moyenne ?

2. Faire une phrase qui interprète le salaire médian français en utilisant les mots : gagnent - euros - moitié - moins - français.

3. Quelles sont les valeurs qui ont un fort impact sur la moyenne mais qui n'ont que peu d'influence sur la médiane ?

4. Comment expliquer un tel écart entre la moyenne et la médiane ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

62
[Communiquer.]

Aiko emménage dans une nouvelle ville et souhaite s'inscrire dans un club de cyclotourisme. Elle effectue une recherche sur internet et trouve les résultats suivants.

La moyenne d'âge du Club de l'ouest est de 42,4 ans.
La moyenne d'âge du Club de l'est est de 39,4 ans.

Aiko a 42 ans et habite en centre-ville : elle hésite donc entre ces deux clubs. Son mari lui conseille de s'inscrire dans le Club de l'ouest afin de se sentir plus proche des autres cyclistes et pour lier des amitiés. Dès la première sortie avec le Club de l'ouest, Aiko est déçue, le rythme est trop soutenu : les retraités s'entraînent très régulièrement et les jeunes sont en pleine forme. De plus, elle ne se sent proche de personne. 1. Aiko veut vérifier que les informations trouvées sur internet étaient justes. Calculer les moyennes des deux clubs à l'aide des tableaux d'effectifs qu'elle a récupérés auprès de chaque dirigeant.

Club de l'ouest

Âge	17	18	19	20	21	58	61	63	66	68	69
Effectif	1	3	6	4	3	2	3	4	5	1	3

Club de l'est

Âge	32	34	35	37	40	42	43	45	47	50
Effectif	6	4	3	2	2	5	6	4	2	1

2. Déterminer les médianes des deux séries puis calculer les deux écarts interquartiles.

3. Quels indicateurs auraient dû être affichés sur internet pour donner les meilleures indications sur l'âge des membres de ces clubs ? Justifier.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

63
En EMI
[Communiquer.]

Voici un extrait de l'article du site mobile du journal Le Monde, daté du 5 septembre 2014.

Les inégalités se sont encore accrues aux États-Unis, selon une étude publiée jeudi 4 septembre par la Réserve fédérale (Fed). Les revenus des 10 % les plus riches ont augmenté de 10 % entre 2010 et 2013 pour s'inscrire à 397 500 dollars par an (307 000 euros). Dans le même temps, ceux des 40 % les moins aisés, ajustés de l'inflation, ont décliné, indique le rapport publié tous les trois ans.
Pour les vingt premiers centiles situés au bas de l'échelle, la chute atteint 8 % à 15 200 dollars annuels. Si le revenu moyen global a augmenté de 4 % au cours des trois dernières années, le revenu médian (c'est-à-dire le revenu qui divise la population en deux parties égales : l'une gagnant plus, l'autre moins), lui, a chuté de 5 %. Une tendance qui « correspond avec un accroissement de la concentration des revenus durant cette période », indique la Fed.

1. Pourquoi le revenu médian aux États-Unis a-t-il baissé sur cette période ?

2. Comment le revenu moyen a-t-il pu augmenter malgré la baisse de rémunération des populations les moins aisées pendant cette période ?

3. Que nous indiquent respectivement moyenne et médiane dans cet exemple ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

64
En SVT / En Géographie
[Chercher.]
Chicago et Rome sont situées à la même latitude. Voici les relevés des températures moyennes à la mi-journée des deux villes en 2017.

Mois	J	F	M	A	M	J	J	A	S	O	N	D
Rome en °C	11	16	18	20	23	28	34	36	25	23	16	12
Chicago en °F	32	39	41	57	59	75	82	79	72	57	39	27

Le zoom est accessible dans la version Premium.

1. Calculer la moyenne et l'écart-type pour chacune des deux séries afin de comparer les températures de Rome et de Chicago en 2017.

Aide

Pour convertir les températures, on a \mathrm { T } ^ { \circ } \mathrm { C } = \dfrac { 5 } { 9 } \times \left( \mathrm { T } ^ { \circ } \mathrm { F } - 32 \right).

2. Ouverture SVT et Géographie : Comment expliquer ces différences pour deux villes situées à la même latitude ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

65
Démo
[Raisonner.]

On considère une première série statistique \text{A}_1 d'effectif total n_1, de moyenne m_1 et de médiane \text{Me}_1. Une seconde série statistique \text{A}_2 a pour effectif total n_2, pour moyenne m_2 et pour médiane \text{Me}_2. On considère la série statistique globale \text{A} constituée des valeurs des deux séries \text{A}_1 et \text{A}_2. On note n son effectif total, m sa moyenne et \text{Me} sa médiane. 1. Montrer que l'on a m = \dfrac { n _ { 1 } m _ { 1 } + n _ { 2 } m _ { 2 } } { n _ { 1 } + n _ { 2 } }.

Aide

Il faut commencer par trouver la somme de toutes les valeurs de \text{A}_1 et la somme de celles de \text{A}_2 .

2. Justifier que \text{Me} est comprise entre les valeurs de \text{Me}_1 et \text{Me}_2.

3. Voici les valeurs d'une série \text{A}_1 \: : –1 \: ; 0 et 10. Voici celles d'une série \text{A}_2 \: : 1 \: ; 6 \: ; 8 et 9.
Calculer tous les indicateurs de l'énoncé puis vérifier les résultats des questions précédentes.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

66
En EMI
[Chercher.]
Le journal Le Monde a publié le 28 mai 2018 un article sur l'évolution du nombre de fumeurs de cigarettes en France. Ci-dessous, le graphique tracé à partir des données de l'organisme Santé publique France :

Le zoom est accessible dans la version Premium.

1. La courbe du haut représente l'évolution du nombre de fumeurs au sein du 1^er tercile. Comment ce groupe de Français est-il caractérisé ?

Aide

Que signifie quartile ? Que signifie tercile ?

2. Quelle méthode doit-on utiliser pour constituer ces trois groupes ?

3. Comparer ces trois évolutions.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

67
[Chercher.]
Au milieu du XIX^e siècle, Florence Nightingale présenta le diagramme ci-dessous aux parlementaires anglais et aux hauts fonctionnaires hospitaliers comme rapport sur les causes de décès lors de la guerre de Crimée.

Florence Nightingale Diagramme - Statistiques descriptives

Le zoom est accessible dans la version Premium.

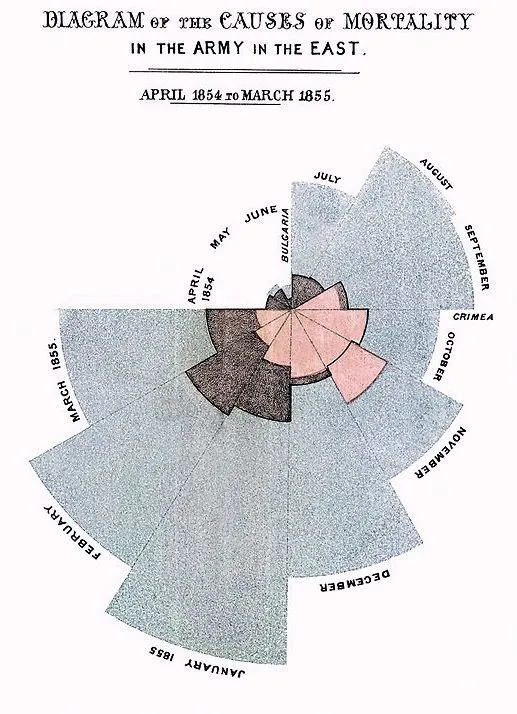
Rose : mort à la bataille. Gris : mort de maladie. Noir : mort pour d'autres causes.

1. Pourquoi les sections correspondant à chaque mois ne sont pas de même taille ?

2. Comment ces diagrammes ont-ils permis à Florence Nightingale d'alerter les parlementaires anglais au sujet de la situation sanitaire au sein de leurs hôpitaux ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

68
[Chercher.]

Lison a relevé toutes les notes qu'elle a obtenues cette année en mathématiques (les notes sont toutes sur 20) :

1^er trimestre : 9 \: ; 11 et 13 \: ;
2^e trimestre : 12 \: ; 15 \: ; 14 et 16 \: ;
3^e trimestre : 10 et 8.

Lison avait prévenu ses parents que sa moyenne annuelle serait de 12. Malheureusement, à la réception du bulletin, cette moyenne annuelle n'est que de 11\text{,}4. 1. Pourquoi Lison s'est-elle trompée ?

2. Comment expliquer cet écart ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Histoire des maths

Le zoom est accessible dans la version Premium.

Florence Nightingale (1820-1910), infirmière, fut également un personnage important du féminisme anglais. Elle a rédigé des rapports qui ont eu un effet profond sur la situation sanitaire dans l'armée, les conditions de vie en Inde, les statistiques médicales et les soins infirmiers.
Elle rassembla des preuves de la mauvaise gestion des hôpitaux et réunit des statistiques sur la mortalité sous forme de diagrammes circulaires. Après la guerre de Crimée (1854-1856), elle se mit à utiliser une version améliorée de ces diagrammes qu'elle appelait coxcomb (crête de coq). Elle les utilisait fréquemment pour présenter des rapports pendant cette guerre aux membres du Parlement. En 1858, elle fut la première femme à être élue membre de la Royal Statistical Society.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

69
[Chercher.]
On a résumé une série statistique à l'aide du tableau des valeurs et des effectifs ci-dessous.

Valeur	-5	0	1	2	6
Effectif	2	5	4	7	8

1. Prévoir, sans calculer les indicateurs, si la moyenne de cette série sera supérieure, inférieure ou égale à la médiane en expliquant le raisonnement.

2. Vérifier cette conjecture par le calcul. Arrondir la moyenne au centième.

3. Déterminer les quartiles et l'écart interquartile.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

70
[Chercher.]
Lorsqu'il y a trop de données à traiter pour une série statistique, on regroupe les valeurs dans des intervalles de type [ a \: ; b [ \ , appelés « classes ».
Dans un lycée, on demande à chaque lycéen le temps nécessaire en minute pour aller de chez eux au lycée. Les données sont retranscrites dans le tableau ci-dessous.

Temps	[0 ; 10[	[10 ; 20[	[20 ; 30[	[30 ; 40[	[40 ; 50[	[50 ; 60[
Effectif	245	321	142	110	54	23

1. Combien de lycéens ont été interrogés ?

2. Donner une signification au nombre 142 du tableau.

3. Quelle méthode peut-on imaginer pour connaître le temps de trajet moyen ? Déterminer ce temps à l'aide de cette méthode.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Club de Maths

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

71
Défi

Le tableau ci-dessous résume une série statistique dont la moyenne est 1\text{,}5 \: ; la médiane est 2 et l'écart interquartile vaut 5.

Valeur	-1	0	2	4	Total
Effectif					20

Compléter le tableau des effectifs ci-dessus en respectant les valeurs des indicateurs.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

72
Énigme

Simone a plusieurs sortes d'animaux dont :

un seul n'est pas un mammifère ;
exactement 2 ne sont pas des chats ;
exactement 3 ne sont pas des chiens ;
exactement 4 ne sont pas des poules.

Le zoom est accessible dans la version Premium.

Établir la liste et le nombre d'animaux de Simone.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

73
Énigme

Yasmine et Mehmet, deux enseignants de mathématiques, bavardent en salle des professeurs. Yasmine demande à Mehmet de lui rappeler l'âge de ses trois enfants. Il lui répond :
« Le produit de leurs trois âges est égal à 36.
— D'accord, que peux-tu me dire de plus ?
— La somme de leurs trois âges est égale à la note de cet élève écrite sur cette copie. »
Yasmine regarde la note, réfléchit, puis répond :
« Très bien, merci, mais je ne suis toujours pas en mesure de savoir.
— L'aînée est une fille.
— C'est bon, je sais ! »

Comment Yasmine a-t-elle pu savoir quels âges avaient les trois enfants de Mehmet ? Quels sont ces âges ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

74
Défi

La moyenne de trois nombres x \: ; y et z est 3.
On sait aussi que la moyenne de x et y est 1\text{,}5.
Enfin, la moyenne de y et z est égale à -2 .
Déterminer la valeur des trois nombres x \: ; y et z .

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercices transversaux en lien avec ce chapitre :

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

Oups, une coquille

j'ai une idée !

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.