Moyenne et écart-type

DIFFÉRENCIATION

◉◉◉ Parcours 1 : exercices 34 ; 35 ; 37 ; 40 ; 48 ; 51 ; 57 et 62
◉◉◉ Parcours 2 : exercices 33 ; 44 ; 45 ; 47 ; 49 ; 54 ; 61 et 68
◉◉◉ Parcours 3 : exercices 42 ; 43 ; 50 ; 58 ; 60 ; 63 et 65

47

[Chercher.] ◉◉◉
Le tableau suivant donne des informations sur l’ensemble des coupes du monde de football (source : UEFA).

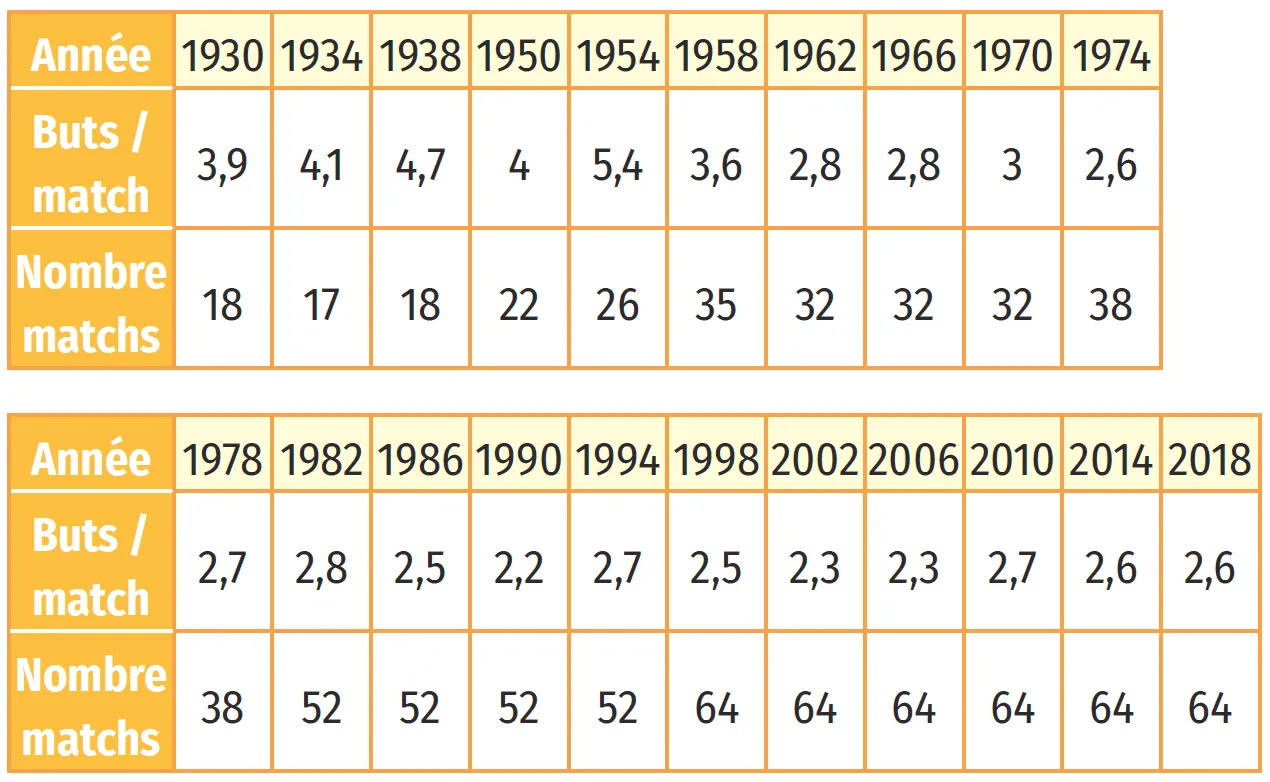
1. Déterminer le nombre moyen de buts marqués lors des coupes du monde, ainsi que l’écart-type correspondant.

2. En 2018, lors des matchs joués par la France, il y a eu une moyenne de $2\text{,}9$ buts. Pour l’Allemagne, cette moyenne est de $2.$ Commenter.

48

[Calculer.] ◉◉◉
Une SCOP (Société coopérative ouvrière de production) a dégagé des bénéfices cette année. Pour l’an prochain, elle décide de multiplier tous les salaires mensuels par 1,1 puis de les augmenter de 100 €. Cette année le salaire moyen était de 1 700 €.

1. Quel sera le salaire moyen l’an prochain ?

2. Estimer comment va évoluer l’écart-type.

49

[Chercher.] ◉◉◉
Sacha compte le nombre de mails reçus chaque jour pendant un an. Les résultats sont donnés dans le tableau ci-dessous.

$x_i$	1	2	3	4	5	6	7	8	9	10
$n_i$	24	18	32	52	65	78	31	27	25	13

1. Calculer une valeur approchée de la moyenne $\overline { x }$ et de l’écart-type $\sigma$ de cette série.

2. Si leur effectif augmentait, donner les valeurs de $x_i$ qui feraient :
a. baisser en même temps $\overline { x }$ et $\sigma \:;$

b. augmenter en même temps $\overline { x }$ et $\sigma.$

50

[Représenter.] ◉◉◉
On représente trois séries statistiques par des diagrammes en barres donnés ci-dessous.

Série 1

Série 2

Série 3

Associer chacun de ces diagrammes aux valeurs des moyennes et écart-types suivantes (arrondies au dixième près).
1. $35\text{,}1$ et $3\text{,}6$
Série 1Série 2Série 3
2. $34\text{,}6$ et $1\text{,}5$
Série 1Série 2Série 3
3. $34\text{,}8$ et $3\text{,}2$
Série 1Série 2Série 3

51

[Chercher.] ◉◉◉
Deux nouvelles applications pour smartphone semblent proposer les mêmes services. Avant d’installer l’une des deux, Nirina désire connaître le vote des utilisateurs (5 étant la meilleure note).

Vote app. 1	0	1	2	3	4	5
Effectif	0	3	7	109	428	419

Vote app. 2	0	1	2	3	4	5
Effectif	58	53	0	44	399	474

1. Déterminer l’effectif total de votants, la moyenne et l’écart-type du vote pour chacune des deux applications.

2. À l’aide des valeurs trouvées à la question 1., quelle application peut-on conseiller à Nirina ?

52

[Chercher.]
Une professeure de mathématiques a corrigé son paquet de 50 copies du bac notées sur 20. Le centre d’examen l’informe que la moyenne des correcteurs est de 10/20. Elle doit vérifier si son paquet est plutôt meilleur ou moins bon que la moyenne du centre. Elle a enregistré ses notes dans un tableau. Au bac, les notes sont des nombres entiers.

Valeur	3	4	5	6	7	9	10
Effectif	3	2	5	3	7	8	3

Valeur	11	12	13	15	16	18	19
Effectif	2	6	1	4	3	2	1

1. Entrer les notes dans la calculatrice avec les effectifs de copies associés.
2. Afficher sur la calculatrice l’ensemble des indicateurs statistiques puis donner la moyenne et l’écart-type. Où se situe son paquet de copies en comparaison à ceux du centre d’examen ? Arrondir au centième.

3. Elle reprend ses copies et s’aperçoit qu’elle a enregistré un 9 alors que le candidat avait 19. Modifier les deux effectifs concernés puis afficher de nouveau la moyenne. Au final, que peut-elle penser de son paquet ?

53

PYTHON

[Raisonner.]
La moyenne du 1^er trimestre est calculée sur la base de quatre notes sur $20.$ On note $m$ la moyenne que Ronista a obtenue à la fin du trimestre.
1. Exprimer, en fonction de $m,$ la somme des points que Ronista a obtenus sur l’ensemble des $4$ notes.

2. Elle a obtenu $6 \: ;$ $10$ puis 1$2$ lors des trois premiers contrôles. Exprimer, en fonction de $m,$ la note qu’elle a obtenue au dernier contrôle.

3. Compléter le programme ci-dessous qui calcule la note qu’elle doit obtenir au dernier contrôle après avoir entré la moyenne qu’elle souhaite obtenir.

def MoyenneVoulue(m): 
  note = ... 
  if ... > 20:
    return("Impossible.") 
  else:
    return(...) 

4. Créer une fonction sous Python qui utilise comme arguments les trois premières notes obtenues puis la moyenne souhaitée et qui renvoie la dernière note à obtenir.

54

[Communiquer.] ◉◉◉

On a représenté quatre cibles avec l’impact de cinq flèches tirées à l’arc. Chaque couronne a un rayon de 1 unité. Pour chaque tireur, on considère la distance de chaque flèche au centre de la cible.
1. Ci-dessous, associer chaque couple (moyenne ; écart-type) à chaque cible : $(2\text{,}84 \: ; 0\text{,}97) \: ;$ $(0\text{,}79 \: ; 0\text{,}19) \: ;$ $(3\text{,}33 \: ; 0\text{,}55) \: ;$ $(3\text{,}21 \: ; 1\text{,}42).$
2. Associer chacun des quatre tireurs à une cible : un tireur expérimenté, deux tireurs débutants et un tireur ayant mal réglé son viseur.

Couple (moyenne ; écart-type) : Tireur :
DébutantDébutantExpérimentéViseur mal réglé

Couple (moyenne ; écart-type) : Tireur :
DébutantDébutantExpérimentéViseur mal réglé

Couple (moyenne ; écart-type) : Tireur :
DébutantDébutantExpérimentéViseur mal réglé

Couple (moyenne ; écart-type) : Tireur :
DébutantDébutantExpérimentéViseur mal réglé

55

TABLEUR

[Calculer.]
On considère la série statistique donnée par le tableur ci-dessous. On déterminera à l’aide des questions posées la moyenne et l’écart-type de la série.

1. À quoi correspond la valeur $200 \: ?$ Comment l’obtenir ?

2. Quelle formule faut-il entrer en B3 puis étirer vers la droite ?

3. Quelle formule faut-il entrer en H3 pour obtenir la moyenne de la série ?

4. Quelle formule faut-il entrer en B4 puis étirer vers la droite ?

5. Comment obtenir l’écart-type en H4 ?

56

[Calculer.]
Le tableau ci-dessous récapitule les taux d’audience à la télévision pour six catégories. Par exemple, en 2018, les émissions sportives ont obtenu 36 % de l’audience, notamment grâce aux résultats de l’équipe de France de football lors de la coupe du monde.

	2014	2015	2016	2017	2018
Sport	22	9	23	11	36
Information	6	4	2	13	9
Fiction FR	18	32	37	42	26
Fiction US	32	37	2	4	18
Divertissement	16	14	29	22	7
Cinéma	6	4	7	8	4
Total	100	100	100	100	100

1. Pour chaque catégorie :
a. calculer la moyenne des audiences obtenues de l’année 2014 jusqu’à l’année 2018 ;

b. déterminer l’écart-type à la calculatrice.

2. Comment interpréter ces différents résultats ?

57

[Calculer.] ◉◉◉
Durant l’année scolaire 2018-2019, Ismaël a été lycéen en terminale S, spécialité SVT. Il a utilisé ses moyennes annuelles pour faire une estimation du résultat qu’il pourrait obtenir au bac. Pour cela, il a utilisé les coefficients utilisés pour le bac cette année-là.
N.B : La note de français est celle qu’il a obtenue lors de l’épreuve anticipée du bac en juin 2018.

Matière	Maths	Ph.-Ch.	SVT	Franç.	Hist.-Géo.	Philo	LV1	LV2	EPS
Coeff.	7	6	8	4	3	3	3	2	2
Moyenne	11,1	12,3	13,8	10,5	11,6	10,4	12,7	9,2	9,9

Estimer la note qu’il a obtenu au bac sachant qu'il a été aussi stable qu’il l’a été durant l’année. Arrondir au centième.

58

[Calculer.] ◉◉◉
On considère une série d’effectif total $\mathrm { N } = n _ { 1 } + n _ { 2 }.$
$n _ { 1 }$ éléments sont égaux à la valeur $x _ { 1 }$ et $n _ { 2 }$ éléments ont pour valeur $x _ { 2 }.$
1. Exprimer la moyenne $m$ de cette série.

2. On sélectionne $n _ { 3 }$ éléments parmi ceux ayant pour valeur $x _ { 1 }$ et on change leur valeur par la valeur $x _ { 3 }.$ On considère $n _ { 3 } \lt n _ { 1 }.$ Exprimer la nouvelle moyenne $m^\prime$ en fonction de $m$ et des autres données de l’énoncé.

59

[Calculer.]
Lors de la Coupe du monde de volley-ball féminin Japon 2018, on donne les tailles des joueuses des équipes des États-Unis et de la Chine.
États-Unis (en pieds-pouces) : $5’11” \: ;$ $5’9” \: ;$ $5’7” \: ;$ $6’1” \: ;$ $5’10” \: ;$ $6’2” \: ;$ $6’2” \: ;$ $6’2” \: ;$ $6’4” \: ;$ $6’2” \: ;$ $6’0” \: ;$ $6’4”.$
Chine (en m) : $1\text{,}9 \: ;$ $1\text{,}81 \: ;$ $1\text{,}92 \: ;$ $1\text{,}89 \: ;$ $1\text{,}9 \: ;$ $1\text{,}81 \: ;$ $1\text{,}67 \: ;$ $1\text{,}82 \: ;$ $1\text{,}72 \: ;$ $1\text{,}87 \: ;$ $1\text{,}96 \: ;$ $1\text{,}93 \: ;$ $1\text{,}82 \: ;$ $1\text{,}84 \: ;$ $1\text{,}89 \: ;$ $1\text{,}8 \: ;$ $1\text{,}91 \: ;$ $1\text{,}9.$
(sources : USA Volley-Ball et Wikipedia.)

1. Calculer la taille moyenne et l’écart-type de l’équipe chinoise en mètres.

2. On sait que $1’ = 1$ pied $= 12$ pouces $= 12”$.
a. Convertir chaque taille de l’équipe des États-Unis en pouces.

b. Calculer la taille moyenne et l’écart-type de l’équipe états-unienne en pouces.

3. Sachant que $1” = 2\text{,}54$ cm, comparer les tailles des deux équipes.

60

[Chercher.] ◉◉◉
Ci-dessous, on a deux copies d’écran de calculatrices qui donnent des résumés statistiques de deux séries de valeurs entières comprises entre $0$ et $5.$

Trouver une série qui convient à chaque écran.