Chapitre 11
Cours
Modélisation d'interactions fondamentales
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Charge électrique, électrisation, loi de Coulomb
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ALa charge électrique
Déjà dans l'Antiquité, on savait qu'en frottant un morceau d'ambre avec de la fourrure ou de la laine, il pouvait attirer à lui des objets légers. Cette attraction a pour origine les propriétés électriques de la matière.
Selon les matières mises en jeu, une attraction ou une répulsion peuvent être observées. Il existe deux caractères électriques, liés à deux types de charges électriques : positive et négative.
Des charges de même signe se repoussent alors que des charges de signes opposés s'attirent (doc. 2).
Toute charge est égale à un multiple de la charge élémentaire e= 1,602 \times 10-19 C. L'unité du système international de la charge est le coulomb, noté C :
Selon les matières mises en jeu, une attraction ou une répulsion peuvent être observées. Il existe deux caractères électriques, liés à deux types de charges électriques : positive et négative.
Des charges de même signe se repoussent alors que des charges de signes opposés s'attirent (doc. 2).
Toute charge est égale à un multiple de la charge élémentaire e= 1,602 \times 10-19 C. L'unité du système international de la charge est le coulomb, noté C :
- un électron porte une charge de -e et un proton une charge de +e ;
- la cohésion de la matière est assurée par les charges des particules qui la constituent, même si la matière est lacunaire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1 Table triboélectrique

Cette table permet de déterminer le matériau qui cède et celui qui reçoit les électrons lors d'une électrisation par frottement entre eux
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2 Attraction, répulsion électrique

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BÉlectrisation
1. Électrisation par frottement
Lors du frottement entre l'ambre et la laine, la laine donne certains de ses électrons à l'ambre. Les deux matériaux sont ici électrisés par frottement, l'ambre devient électriquement négatif et la laine électriquement positive.
2. Électrisation par contact
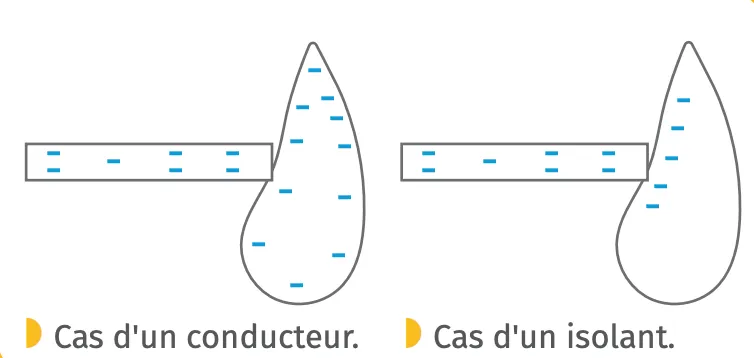
Un objet chargé électriquement, mis en contact avec un objet neutre, lui transfère une partie de sa charge (doc. 3). Si le matériau est :
3. Électrisation par influence
Lorsque l'on approche un objet chargé :
Lors du frottement entre l'ambre et la laine, la laine donne certains de ses électrons à l'ambre. Les deux matériaux sont ici électrisés par frottement, l'ambre devient électriquement négatif et la laine électriquement positive.
2. Électrisation par contact
Un objet chargé électriquement, mis en contact avec un objet neutre, lui transfère une partie de sa charge (doc. 3). Si le matériau est :
- conducteur, alors la charge se répartit sur toute sa surface ;
- isolant, alors la charge reste au niveau de la zone de contact.
3. Électrisation par influence
Lorsque l'on approche un objet chargé :
- d'un matériau conducteur : la répartition des charges est modifiée dans le conducteur ;
- d'une substance dipolaire : les dipôles s'orientent dans le sens du champ électrostatique créé par l'objet (doc. 4).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Charge électrique : propriété de la matière lui permettant d'interagir avec un champ électromagnétique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 3 Électrisation par contact

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CLoi de Coulomb
Au XVIIIe siècle, Charles-Augustin Coulomb (1736-1806) effectue des mesures de forces électrostatiques sur des sphères chargées à l'aide d'une balance de torsion.
Il démontre que la valeur de cette force F_{\mathrm{e}} est proportionnelle aux charges électriques mises en jeu, et proportionnelle à l'inverse du carré de la distance séparant le centre des sphères :
Il démontre que la valeur de cette force F_{\mathrm{e}} est proportionnelle aux charges électriques mises en jeu, et proportionnelle à l'inverse du carré de la distance séparant le centre des sphères :
F_{\mathrm{e}}=k \cdot \dfrac{\vert{q_{\mathrm{A}}} \cdot q_{\mathrm{B}}\vert}{d_{\mathrm{AB}}^{2}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 4 Électrisation par influence

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 La force gravitationnelle et la force électrostatique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A De l'interaction à la force
Soit deux objets \text{A} et \text{B} qui agissent de manière réciproque l'un sur l'autre : \text{A} agit sur \text{B} et \text{B} agit sur \text{A}, on dit alors que ces objets sont en interaction.
Chaque action est modélisée par une force, elle-même représentée par un vecteur portant quatre caractéristiques : un sens, une direction, une intensité et un point d'application (doc. 5).
Chaque action est modélisée par une force, elle-même représentée par un vecteur portant quatre caractéristiques : un sens, une direction, une intensité et un point d'application (doc. 5).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 5 Représentation des forces

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B La force gravitationnelle
Tous les corps qui ont une masse s'attirent les uns les autres : ce
phénomène est appelé gravitation. Ces actions sont réciproques, on parle donc d'interaction gravitationnelle.
La force modélisant ces actions est appelée force d'attraction gravitationnelle, elle est décrite par la relation :
avec G la constante universelle de la gravitation (G = 6,67 \times 10-11 N·kg-2·m2), m_{\text{A}} et m_{\text{B}} les masses (en kg) des corps \text{A} et \text{B}, et d la distance entre \text{A} et \text{B} exprimée en mètre (m).
\vec{e}_{\mathrm{r}} est le vecteur unitaire porté par la droite \text{(AB)}, orienté de \text{A} vers \text{B.}
L'intensité de la force gravitationnelle est égale à la valeur absolue de la force précédente : F_{\mathrm{g}}=G \cdot \dfrac{m_{\mathrm{A}} \cdot m_{\mathrm{B}}}{d^{2}}.
On remarque que l'action gravitationnelle d'un corps \text{A} sur un corps \text{B} est de même intensité que celle du corps \text{B} sur le corps \text{A.} Ainsi, la Terre attire autant à elle la Lune que la Lune attire à elle la Terre.
La force modélisant ces actions est appelée force d'attraction gravitationnelle, elle est décrite par la relation :
\vec{F}_{\mathrm{g}}(\mathrm{A} / \mathrm{B})=-G \cdot \dfrac{m_{\mathrm{A}} \cdot m_{\mathrm{B}}}{d^{2}} \vec{\mathrm{e}}_{\mathrm{r}}
avec G la constante universelle de la gravitation (G = 6,67 \times 10-11 N·kg-2·m2), m_{\text{A}} et m_{\text{B}} les masses (en kg) des corps \text{A} et \text{B}, et d la distance entre \text{A} et \text{B} exprimée en mètre (m).
\vec{e}_{\mathrm{r}} est le vecteur unitaire porté par la droite \text{(AB)}, orienté de \text{A} vers \text{B.}
L'intensité de la force gravitationnelle est égale à la valeur absolue de la force précédente : F_{\mathrm{g}}=G \cdot \dfrac{m_{\mathrm{A}} \cdot m_{\mathrm{B}}}{d^{2}}.
On remarque que l'action gravitationnelle d'un corps \text{A} sur un corps \text{B} est de même intensité que celle du corps \text{B} sur le corps \text{A.} Ainsi, la Terre attire autant à elle la Lune que la Lune attire à elle la Terre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
➜ Attention au référentiel choisi ! Habituellement, l'origine du repère spatial est prise au centre du corps de masse la plus grande.
Par exemple, lors de l'étude de l'interaction gravitationnelle entre le Soleil et la Terre, on se place généralement dans le référentiel héliocentrique, donc :
\vec{F}_{\mathrm{g}}(\text {Soleil/Terre})=-G \cdot \dfrac{m_{\text {Soleil}} \cdot m_{\text {Terre}}}{d^{2}} \vec{e}_{\mathrm{r}}
\vec{F}_{\mathrm{g}}(\text {Terre} / \text {Soleil})=G \cdot \dfrac{m_{\text {Soleil}} \cdot m_{\text {Terre}}}{d^{2}} \vec{e}_{\mathrm{r}}
avec \vec{e}_{\text{r}} vecteur unitaire orienté du Soleil vers la Terre.
Par exemple, lors de l'étude de l'interaction gravitationnelle entre le Soleil et la Terre, on se place généralement dans le référentiel héliocentrique, donc :
\vec{F}_{\mathrm{g}}(\text {Soleil/Terre})=-G \cdot \dfrac{m_{\text {Soleil}} \cdot m_{\text {Terre}}}{d^{2}} \vec{e}_{\mathrm{r}}
\vec{F}_{\mathrm{g}}(\text {Terre} / \text {Soleil})=G \cdot \dfrac{m_{\text {Soleil}} \cdot m_{\text {Terre}}}{d^{2}} \vec{e}_{\mathrm{r}}
avec \vec{e}_{\text{r}} vecteur unitaire orienté du Soleil vers la Terre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 6 Mesure de G par Cavendish
John Cavendish (1732-1796), avec 4 masses, un fil, un miroir et un rayon lumineux, a mesuré la constante de gravité G avec une remarquable précision.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
C La force électrostatique
Tous les corps possédant une charge électrique s'attirent ou se
repoussent de manière réciproque.
La force modélisant ces actions est appelée force électrostatique, elle est décrite par la relation :
avec k = 8,99 \times 109 N·m2·C-2, q_{\text{A}} et q_{\text{B}} les valeurs des charges électriques portées respectivement par les corps \text{A} et \text{B} et exprimées en coulomb (C), et d la distance entre \text{A} et \text{B} exprimée en mètre (m).
L'intensité de cette force est égale à la valeur absolue de la relation précédente : F_{\mathrm{e}}(\mathrm{A} / \mathrm{B})=k \cdot \dfrac{\vert q_{\mathrm{A}} \cdot q_{\mathrm{B}}\vert}{d^{2}}.
On remarque ici aussi que l'action électrostatique d'un corps \text{A} sur un corps \text{B} est de même intensité que celle du corps \text{B} sur le corps \text{A} (doc. 7).
La force modélisant ces actions est appelée force électrostatique, elle est décrite par la relation :
\vec{F}_{\mathrm{e}}(\mathrm{A} / \mathrm{B})=k \cdot \dfrac{q_{\mathrm{A}} \cdot q_{\mathrm{B}}}{d^{2}} \vec{e}_{\mathrm{r}}
avec k = 8,99 \times 109 N·m2·C-2, q_{\text{A}} et q_{\text{B}} les valeurs des charges électriques portées respectivement par les corps \text{A} et \text{B} et exprimées en coulomb (C), et d la distance entre \text{A} et \text{B} exprimée en mètre (m).
L'intensité de cette force est égale à la valeur absolue de la relation précédente : F_{\mathrm{e}}(\mathrm{A} / \mathrm{B})=k \cdot \dfrac{\vert q_{\mathrm{A}} \cdot q_{\mathrm{B}}\vert}{d^{2}}.
On remarque ici aussi que l'action électrostatique d'un corps \text{A} sur un corps \text{B} est de même intensité que celle du corps \text{B} sur le corps \text{A} (doc. 7).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 7 Attraction, répulsion électrique

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
➜ Attention à bien vérifier le signe des charges, cela a une conséquence directe sur l'orientation des forces mises en jeu !
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3 Le champ gravitationnel et le champ électrostatique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A Les champs
1. Généralités
Un champ représente la cartographie dans l'espace d'une grandeur physique.
On définit deux types de champs :
2. Étude d'un champ vectoriel
Pour dessiner un champ vectoriel, on représente dans l'espace les vecteurs des grandeurs qui nous intéressent.
Afin de mieux visualiser un champ vectoriel, on trace les lignes de champ. Ce sont les courbes qui suivent les vecteurs en respectant leur direction : elles sont tangentes en tout point au vecteur du champ.
Plus les lignes de champ sont proches les unes des autres, plus le champ est intense dans la zone considérée.
Un champ représente la cartographie dans l'espace d'une grandeur physique.
On définit deux types de champs :
- les champs scalaires dont la grandeur cartographiée est scalaire, par exemple les champs de température et de pression ;
- les champs vectoriels dont la grandeur cartographiée est vectorielle, par exemple les champs de vitesse (vent), gravitationnel et électrostatique (doc. 8).
2. Étude d'un champ vectoriel
Pour dessiner un champ vectoriel, on représente dans l'espace les vecteurs des grandeurs qui nous intéressent.
Afin de mieux visualiser un champ vectoriel, on trace les lignes de champ. Ce sont les courbes qui suivent les vecteurs en respectant leur direction : elles sont tangentes en tout point au vecteur du champ.
Plus les lignes de champ sont proches les unes des autres, plus le champ est intense dans la zone considérée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 8 Champ scalaire de température

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Champ : cartographie des valeurs d'une grandeur dans l'espace.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Champ gravitationnel
Tous les corps ayant une masse s'attirent les uns les autres.
Afin de décrire l'action gravitationnelle d'une masse en particulier dans une zone spatiale donnée, on fixe une masse et on représente le champ gravitationnel qu'elle crée.
La valeur du champ gravitationnel créé par une masse m peut être déterminée à partir de la relation \overrightarrow{\mathcal{G}}=G \cdot \dfrac{m}{d^{2}} \vec{e}_{\text{r}} G est la constante universelle de la gravitation (G = 6,67 \times 10-11 N·kg-2·m2).
On appelle couramment « champ de pesanteur terrestre », le champ gravitationnel de la Terre à sa surface (doc. 9).
Afin de décrire l'action gravitationnelle d'une masse en particulier dans une zone spatiale donnée, on fixe une masse et on représente le champ gravitationnel qu'elle crée.
La valeur du champ gravitationnel créé par une masse m peut être déterminée à partir de la relation \overrightarrow{\mathcal{G}}=G \cdot \dfrac{m}{d^{2}} \vec{e}_{\text{r}} G est la constante universelle de la gravitation (G = 6,67 \times 10-11 N·kg-2·m2).
On appelle couramment « champ de pesanteur terrestre », le champ gravitationnel de la Terre à sa surface (doc. 9).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 9 Champ gravitationnel

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CLe champ électrostatique
Tous les objets portant une charge repoussent ou attirent tous les autres objets portant une charge électrique.
Afin de décrire l'action électrostatique d'une charge électrique dans une zone spatiale donnée, on se place du point de vue de cette charge et on représente le champ électrostatique créé (doc. 10).
La valeur du champ électrostatique créé par une charge q en un point peut être déterminée à partir de la relation vectorielle :
\vec{E}=k \cdot \dfrac{q}{d^{2}} \vec{e}_{\text{r}} où k= 9,0 \times 109 N·m2·C-2.
Afin de décrire l'action électrostatique d'une charge électrique dans une zone spatiale donnée, on se place du point de vue de cette charge et on représente le champ électrostatique créé (doc. 10).
La valeur du champ électrostatique créé par une charge q en un point peut être déterminée à partir de la relation vectorielle :
\vec{E}=k \cdot \dfrac{q}{d^{2}} \vec{e}_{\text{r}} où k= 9,0 \times 109 N·m2·C-2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
➜ L'unité d'un champ dépend de la grandeur cartographiée :
- l'unité de \mathcal{G} est le newton par kilogramme N·kg-1 ou en m·s‑2 ;
- l'unité de E est le newton par coulomb N·C-1 ou en V·m-1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 10 Champ électrostatique créé par une charge électrique

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

