Chapitre 2
Cours 3
Étude des fonctions polynômes du second degré
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le plan est muni d'un repère orthonormé. f est une fonction polynôme du second
degré : f ( x ) = a x ^ { 2 } + b x + c = a ( x - \alpha ) ^ { 2 } + \beta.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ASens de variation d'une fonction polynôme du second degré
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
1. Si a \lt 0 , alors f est croissante sur ] - \infty \: ; \alpha ] et décroissante sur [ \alpha \: ; + \infty [.

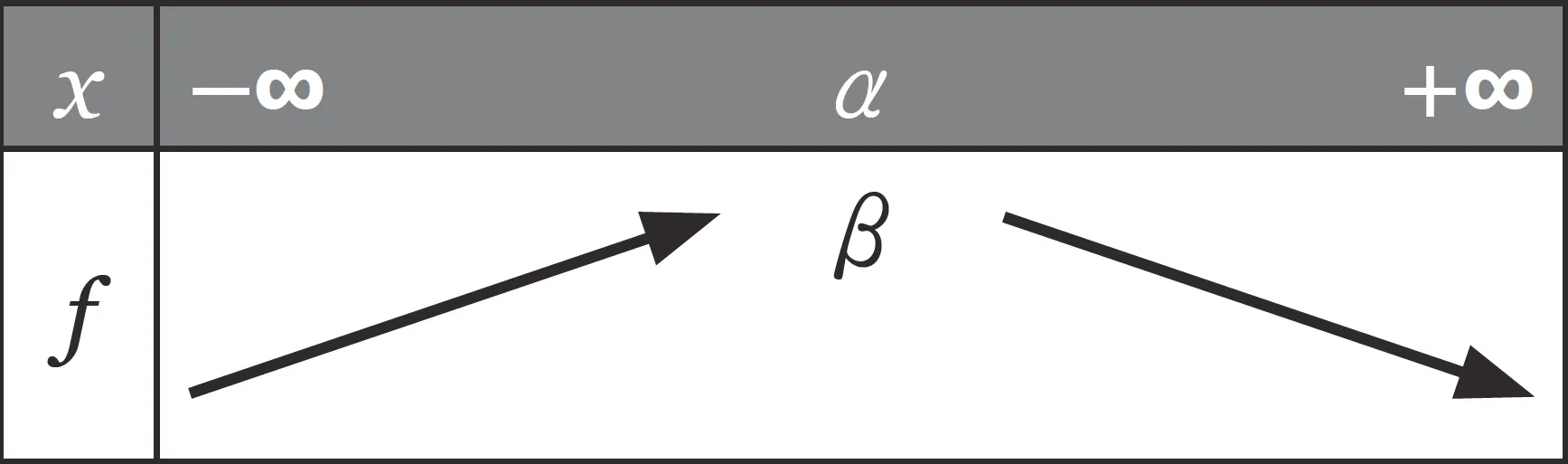
2. Si a \gt 0 , alors f est décroissante sur ] - \infty \: ; \alpha ] et croissante sur [ \alpha \: ; + \infty [.

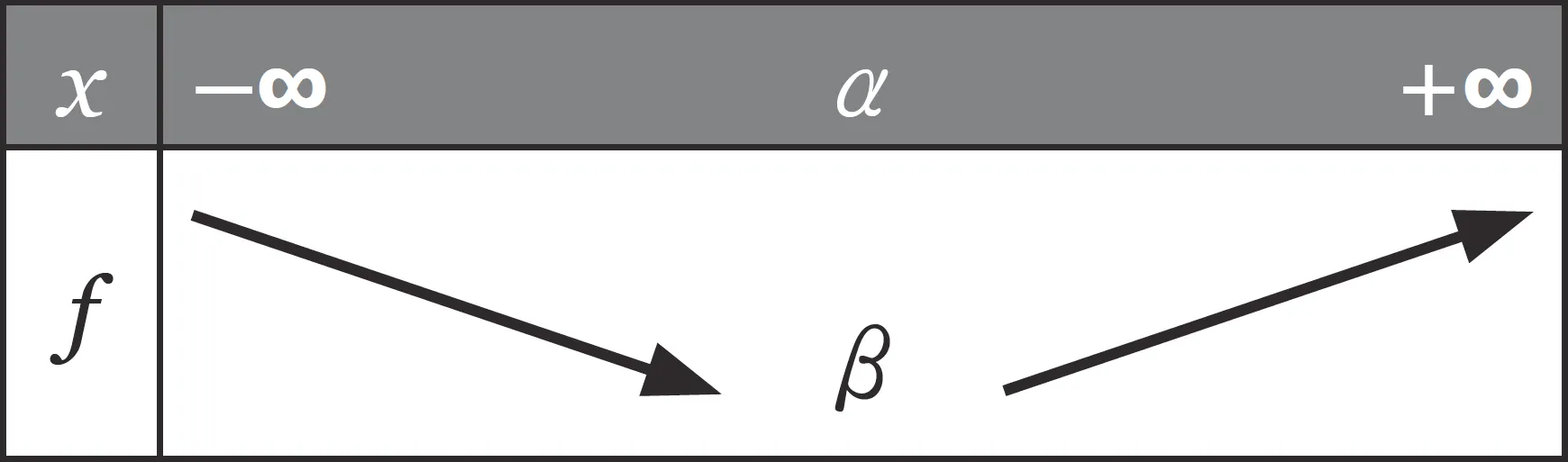


2. Si a \gt 0 , alors f est décroissante sur ] - \infty \: ; \alpha ] et croissante sur [ \alpha \: ; + \infty [.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour étudier les variations d'une fonction polynôme du second degré, on utilise la forme
canonique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On dit que la parabole est « tournée vers le haut » lorsque a \gt 0 et « tournée vers le bas » lorsque a \lt 0 .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
1. Soit a \lt 0.
Sur l'intervalle ] - \infty \: ; \alpha ] :
u et v sont deux réels tels que u \lt v \leqslant \alpha donc u - \alpha \lt v - \alpha \leqslant 0.
Ainsi : ( u - \alpha ) ^ { 2 } \gt ( v - \alpha ) ^ { 2 } puisque la fonction carré est décroissante sur ] - \infty \: ; 0 ].
a ( u - \alpha ) ^ { 2 } \lt a ( v - \alpha ) ^ { 2 } puisque a \lt 0 donc a ( u - \alpha ) ^ { 2 } + \beta \lt a ( v - \alpha ) ^ { 2 } + \beta soit f ( u ) \lt f ( v ).
f est donc croissante sur ] - \infty \: ; \alpha ] .
Sur l'intervalle [ \alpha \: ; + \infty [ \: :
u et v sont deux réels tels que \alpha \leqslant u \lt v donc 0 \leqslant u - \alpha \lt v - \alpha.
Ainsi : ( u - \alpha ) ^ { 2 } \lt ( v - \alpha ) ^ { 2 } puisque la fonction carré est croissante sur [ 0 \: ; + \infty [.
a ( u - \alpha ) ^ { 2 } \gt a ( v - \alpha ) ^ { 2 } puisque a \lt 0 donc a ( u - \alpha ) ^ { 2 } + \beta \gt a ( v - \alpha ) ^ { 2 } + \beta soit f ( u ) \gt f ( v ).
f est donc décroissante sur [ \alpha \: ; + \infty [.
2. On applique un raisonnement analogue lorsque a \gt 0 .
Sur l'intervalle ] - \infty \: ; \alpha ] :
u et v sont deux réels tels que u \lt v \leqslant \alpha donc u - \alpha \lt v - \alpha \leqslant 0.
Ainsi : ( u - \alpha ) ^ { 2 } \gt ( v - \alpha ) ^ { 2 } puisque la fonction carré est décroissante sur ] - \infty \: ; 0 ].
a ( u - \alpha ) ^ { 2 } \lt a ( v - \alpha ) ^ { 2 } puisque a \lt 0 donc a ( u - \alpha ) ^ { 2 } + \beta \lt a ( v - \alpha ) ^ { 2 } + \beta soit f ( u ) \lt f ( v ).
f est donc croissante sur ] - \infty \: ; \alpha ] .
Sur l'intervalle [ \alpha \: ; + \infty [ \: :
u et v sont deux réels tels que \alpha \leqslant u \lt v donc 0 \leqslant u - \alpha \lt v - \alpha.
Ainsi : ( u - \alpha ) ^ { 2 } \lt ( v - \alpha ) ^ { 2 } puisque la fonction carré est croissante sur [ 0 \: ; + \infty [.
a ( u - \alpha ) ^ { 2 } \gt a ( v - \alpha ) ^ { 2 } puisque a \lt 0 donc a ( u - \alpha ) ^ { 2 } + \beta \gt a ( v - \alpha ) ^ { 2 } + \beta soit f ( u ) \gt f ( v ).
f est donc décroissante sur [ \alpha \: ; + \infty [.
2. On applique un raisonnement analogue lorsque a \gt 0 .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Cas a \lt 0

Cas a \gt 0


Cas a \gt 0

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On peut aussi utiliser la symétrie de la courbe par rapport à la droite d'équation x = a .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
f est une fonction polynôme du second degré définie sur \mathbb { R } par f ( x ) = 3 - ( x + 2 ) ^ { 2 }. En détaillant les étapes, déterminer les variations de f sur ] - \infty \: ; - 2 ].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Repérer les valeurs de a, \alpha et \beta pour connaître les variations de f sur \mathbb { R }.
- Prendre deux réels u et v tels que u \lt v \leqslant \alpha.
- Repérer les priorités de calcul, puis effectuer les calculs étape par étape.
- Utiliser les variations de la fonction carré.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
a = - 1 \lt 0 , \alpha = - 2 et \beta = 3.
Montrons que f est croissante sur ] - \infty \: ; - 2 ]. On considère deux réels u et v tels que u \lt v \leqslant - 2.
u + 2 \lt v + 2 \leqslant 0
\Leftrightarrow ( u + 2 ) ^ { 2 } > ( v + 2 ) ^ { 2 } car la fonction carré est décroissante sur ] - \infty \: ; 0 ]
\Leftrightarrow - ( u + 2 ) ^ { 2 } \lt - ( v + 2 ) ^ { 2 } car on multiplie par –1
\Leftrightarrow 3 - ( u + 2 ) ^ { 2 } \lt 3 - ( v + 2 ) ^ { 2 }
\Leftrightarrow f ( u ) \lt f ( v )
f est bien croissante sur ] - \infty \: ; -2 ].
Montrons que f est croissante sur ] - \infty \: ; - 2 ]. On considère deux réels u et v tels que u \lt v \leqslant - 2.
u + 2 \lt v + 2 \leqslant 0
\Leftrightarrow ( u + 2 ) ^ { 2 } > ( v + 2 ) ^ { 2 } car la fonction carré est décroissante sur ] - \infty \: ; 0 ]
\Leftrightarrow - ( u + 2 ) ^ { 2 } \lt - ( v + 2 ) ^ { 2 } car on multiplie par –1
\Leftrightarrow 3 - ( u + 2 ) ^ { 2 } \lt 3 - ( v + 2 ) ^ { 2 }
\Leftrightarrow f ( u ) \lt f ( v )
f est bien croissante sur ] - \infty \: ; -2 ].
Pour s'entraîner
Exercices p. 59 et p. 63
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BExtremum d'une fonction polynôme du second degré
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
1. Si a \lt 0 , alors f admet pour maximum \beta sur \mathbb { R }, atteint au point d'abscisse \alpha.
2. Si a \gt 0 , alors f admet pour minimum \beta sur \mathbb { R }, atteint au point d'abscisse \alpha.
2. Si a \gt 0 , alors f admet pour minimum \beta sur \mathbb { R }, atteint au point d'abscisse \alpha.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Cas a \lt 0


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On retrouve les coordonnées du sommet \text{S} ( \alpha \: ; \beta ) de la parabole \mathcal { P }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Cas a \gt 0


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
1. On considère le cas a \lt 0.
Pour tout réel x , on a : ( x - \alpha ) ^ { 2 } \geqslant 0 donc
a ( x - \alpha ) ^ { 2 } \leqslant 0 car a \lt 0 . D'où a ( x - \alpha ) ^ { 2 } + \beta \leqslant \beta soit f ( x ) \leqslant \beta.
De plus : f ( \alpha ) = a ( \alpha - \alpha ) ^ { 2 } + \beta = \beta.
\beta est donc un maximum de f sur \mathbb { R }, atteint au point d'abscisse \alpha.
2. On applique un raisonnement analogue lorsque a \gt 0 .
Pour tout réel x , on a : ( x - \alpha ) ^ { 2 } \geqslant 0 donc
a ( x - \alpha ) ^ { 2 } \leqslant 0 car a \lt 0 . D'où a ( x - \alpha ) ^ { 2 } + \beta \leqslant \beta soit f ( x ) \leqslant \beta.
De plus : f ( \alpha ) = a ( \alpha - \alpha ) ^ { 2 } + \beta = \beta.
\beta est donc un maximum de f sur \mathbb { R }, atteint au point d'abscisse \alpha.
2. On applique un raisonnement analogue lorsque a \gt 0 .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
f est une fonction polynôme du second degré définie sur \mathbb { R } par f ( x ) = - 2 + 3 ( x - 1 ) ^ { 2 }.
Déterminer l'extremum de f sur \mathbb { R }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Repérer les valeurs de a , \alpha et \beta pour connaître la nature et la valeur de l'extremum de f .
- Écrire que, pour tout réel x , ( x - \alpha ) ^ { 2 } \geqslant 0.
- Repérer les priorités de calcul puis effectuer les calculs étape par étape.
- Écrire f ( \alpha ) = \beta.
- Conclure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
Pour tout réel x , on a :
( x - 1 ) ^ { 2 } \geqslant 0
\Leftrightarrow 3 ( x - 1 ) ^ { 2 } \geqslant 0
\Leftrightarrow - 2 + 3 ( x - 1 ) ^ { 2 } \geqslant - 2
\Leftrightarrow f ( x ) \geqslant - 2.
De plus : f ( 1 ) = - 2 + 3 ( 1 - 1 ) ^ { 2 } = - 2.
-2 est donc le minimum de f sur \mathbb { R }, atteint en x = 1 .
Pour s'entraîner
Exercices et p. 63
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CSigne d'une fonction polynôme du second degré
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode
Pour étudier le signe d'une fonction polynôme du second degré, on utilise la forme
factorisée puis on dresse un tableau de signes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le cas général (notamment lorsque f n'est pas factorisable) sera étudié dans le chapitre 3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
f est la fonction définie sur \mathbb { R } par f ( x ) = - 3 ( x - 1 ) ( x + 2 ).
Le tableau de signes de f est :

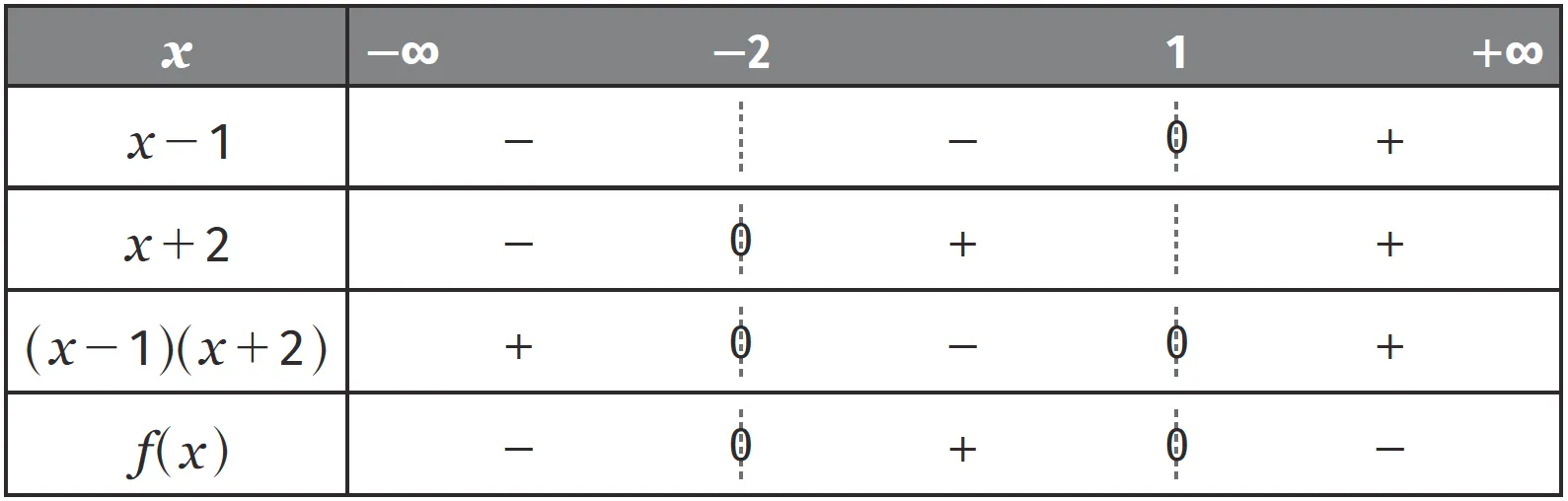
Le tableau de signes de f est :


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
f et g sont définies sur \mathbb { R } par f ( x ) = 3 x ^ { 2 } - 2 x + 5 et g ( x ) = 7 x + 17.
1. Démontrer que, pour tout réel x , f ( x ) - g ( x ) = 3 ( x - 4 ) ( x + 1 ).
2. Étudier la position relative des courbes représentatives C_f et C_g des fonctions f et g .
1. Démontrer que, pour tout réel x , f ( x ) - g ( x ) = 3 ( x - 4 ) ( x + 1 ).
2. Étudier la position relative des courbes représentatives C_f et C_g des fonctions f et g .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Déterminer l'expression de f - g puis développer la forme donnée.
- Étudier le signe de la forme factorisée de f - g en utilisant un tableau de signes.
- Conclure :
- lorsque f - g est positive, C_f est au-dessus de C_g .
- lorsque f - g est négative, C_f est en dessous de C_g .
- lorsque f - g est nulle, C_f et C_g sont sécantes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
1. Pour tout réel x , on a :
\begin{aligned} f ( x ) - g ( x ) & = 3 x ^ { 2 } - 2 x + 5 - ( 7 x + 17 ) \\ & = 3 x ^ { 2 } - 2 x + 5 - 7 x - 17 \\ & = 3 x ^ { 2 } - 9 x - 12 \end{aligned}
\begin{aligned} \text{et } 3 ( x - 4 ) ( x + 1 ) & = 3 \left( x ^ { 2 } + x - 4 x - 4 \right) \\ & = 3 \left( x ^ { 2 } - 3 x - 4 \right) \\ & = 3 x ^ { 2 } - 9 x - 12 \end{aligned}
Donc, pour tout réel x , f ( x ) - g ( x ) = 3 ( x - 4 ) ( x + 1 ).
2. On obtient :

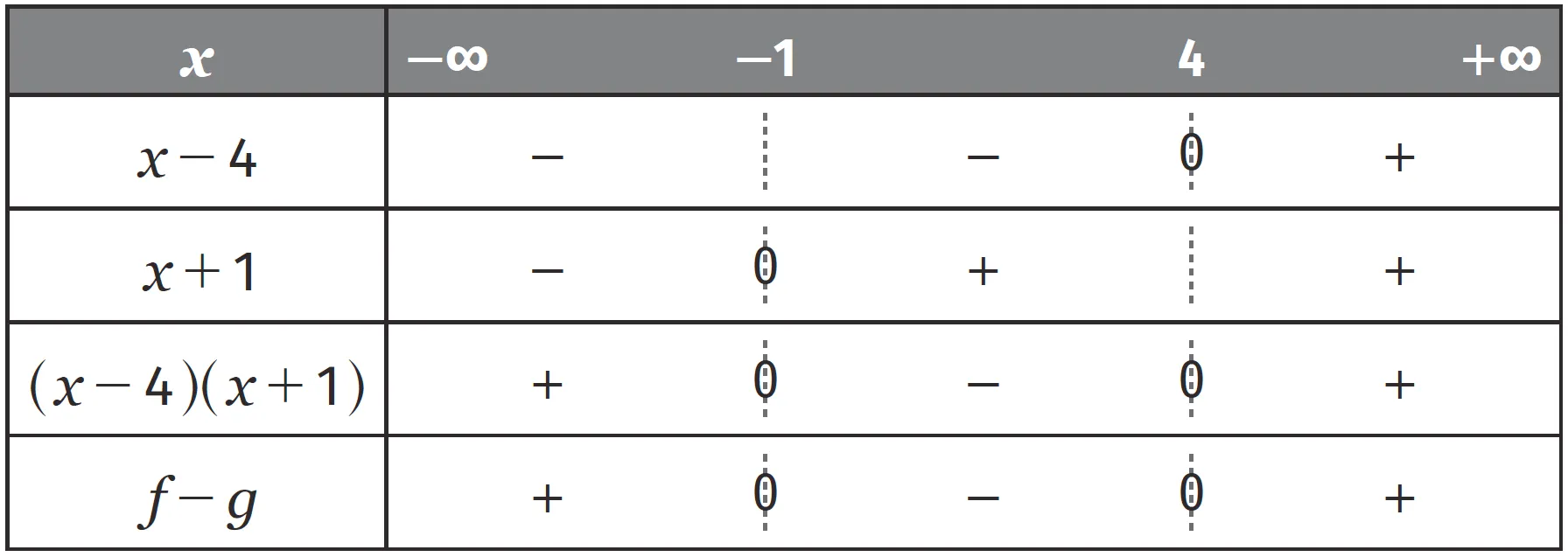
C_f est au-dessus de C_g sur ] - \infty \: ; - 1 ] et sur [ 4 \: ; + \infty [ et en dessous sur [ - 1 \: ; 4 ]. C_f et C_g sont sécantes en -1 et 4.
\begin{aligned} f ( x ) - g ( x ) & = 3 x ^ { 2 } - 2 x + 5 - ( 7 x + 17 ) \\ & = 3 x ^ { 2 } - 2 x + 5 - 7 x - 17 \\ & = 3 x ^ { 2 } - 9 x - 12 \end{aligned}
\begin{aligned} \text{et } 3 ( x - 4 ) ( x + 1 ) & = 3 \left( x ^ { 2 } + x - 4 x - 4 \right) \\ & = 3 \left( x ^ { 2 } - 3 x - 4 \right) \\ & = 3 x ^ { 2 } - 9 x - 12 \end{aligned}
Donc, pour tout réel x , f ( x ) - g ( x ) = 3 ( x - 4 ) ( x + 1 ).
2. On obtient :


C_f est au-dessus de C_g sur ] - \infty \: ; - 1 ] et sur [ 4 \: ; + \infty [ et en dessous sur [ - 1 \: ; 4 ]. C_f et C_g sont sécantes en -1 et 4.
Pour s'entraîner
Exercices p. 59 et p. 64
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

