Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 2
Entraînement 2
Fonctions polynômes du second degré
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
Algo
[Calculer.]
On considère un réel k quelconque. On reprend l'algorithme de l'exercice 43, ci-dessous, afin d'obtenir les solutions éventuelles de l'équation x^2 = k avec k \in \mathbb { R }.
1. Recopier et compléter l'algorithme.
\boxed{
\begin{array} { l } { \text {Définir Solution } (k) \text { : } } \\
\quad \text {Si } k \lt 0 \text { alors : } \\
\quad \quad\text{Retourner « … solution » } \\
\quad \text {Sinon } \\
\quad \quad \text {Si ... alors : } \\
\quad \quad \quad \text {Retourner } 0 \\
\quad \quad \text {Sinon } m \leftarrow \text {...} \\
\quad \quad \quad n \leftarrow \text {...} \\
\quad \quad \quad \text {Retourner } m \text { et } n\\
\quad \quad \text {Fin Si} \\
\quad \text {Fin Si} \\
\end{array}
}
1. Recopier et compléter l'algorithme.
2. a. Programmer cet algorithme à l'aide de la calculatrice ou d'un ordinateur.
b. Tester l'algorithme avec : k = 4 , k = 0 et k = -3 .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52
Algo
[Calculer.]
On considère l'algorithme suivant, où x désigne un réel.
1. Que contient la variable y à la fin de l'exécution de l'algorithme lorsque la variable x contient les valeurs suivantes avant l'exécution :
a. x = 1 \: ?
b. x = - 2 \: ?
c. x = \dfrac { 1 } { 3 } \: ?
2. Donner l'expression de la fonction f qui, à tout nombre réel x , associe le nombre y retourné en fin d'algorithme.
3. Quelle est la nature de cette fonction f \: ?
\boxed{
\begin{array} { l } { y \leftarrow x^2} \\
y \leftarrow 3 y + 5 x + 1 \\
\end{array}
}
1. Que contient la variable y à la fin de l'exécution de l'algorithme lorsque la variable x contient les valeurs suivantes avant l'exécution :
a. x = 1 \: ?
b. x = - 2 \: ?
c. x = \dfrac { 1 } { 3 } \: ?
2. Donner l'expression de la fonction f qui, à tout nombre réel x , associe le nombre y retourné en fin d'algorithme.
3. Quelle est la nature de cette fonction f \: ?
4. Recopier et compléter la traduction suivante de cet algorithme en langage Python.
def fonction_mystere(x): y = ... y = ... return y
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
[Calculer.]
On définit la fonction carré f sur \mathbb { R } par f(x) = x^2.
1. Développer et simplifier ( \sqrt { 5 } - 7 ) ^ { 2 }.
2. En déduire les antécédents du nombre réel ( 54 - 14 \sqrt { 5 } ) par la fonction carré.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54
[Raisonner.]
On considère les fonctions f et g définies sur \mathbb { R } par
f(x) = x^2 et g(x) = 3x. On note respectivement C_f et
C_g les courbes représentatives des fonctions f et g
dans un repère orthonormé.
1. a. Tracer, à l'aide d'une calculatrice ou de GeoGebra, les courbes C_f et C_g.
b. Conjecturer alors les coordonnées des points d'intersection
des courbes C_f et C_g.
2. Démontrer de manière algébrique la conjecture émise.
2. Démontrer de manière algébrique la conjecture émise.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55
Tableur
[Représenter.]
Voici une feuille de calcul d'un tableur.
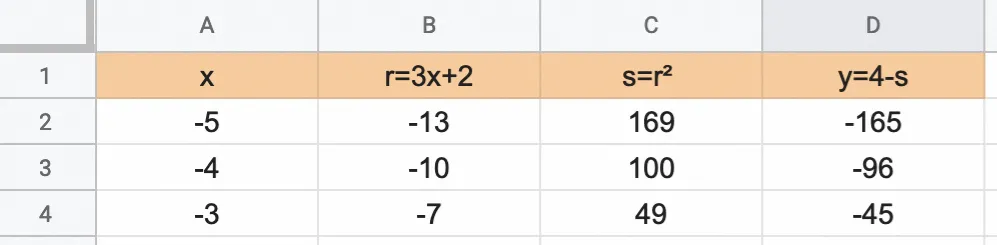
1. Quelles formules sont à saisir pour respecter les notations de la ligne 1 dans les cellules B2, C2 et D2 ?
Le zoom est accessible dans la version Premium.
2. On définit la fonction f sur [ - 5 \: ; 5 ] qui à x associe y .
a. Déterminer l'expression de f en fonction de x .
b. Quelle est la nature de cette fonction ?
a. Déterminer l'expression de f en fonction de x .
b. Quelle est la nature de cette fonction ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56
[Calculer.] f et g sont des fonctions définies sur \mathbb { R } par f ( x ) = ( x - 3 ) ^ { 2 } + 2 et g ( x ) = - 2 ( x - 1 ) ^ { 2 } + 8. Déterminer les éventuels antécédents de 0, de 6 et de 8 par f puis par g . On donnera les valeurs exactes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
[Raisonner.]
On considère les fonctions f et g définies sur \mathbb { R } par f ( x ) = x ^ { 2 } et g ( x ) = 4 x - 4. On note respectivement C_f et C_g les courbes représentatives des fonctions f et g dans un repère orthonormé.
1. a. Tracer, à l'aide d'une calculatrice ou de GeoGebra, les courbes représentatives des fonctions f et g.
GeoGebra
b. Conjecturer alors les coordonnées des éventuels
points d'intersection des courbes C_f et C_g.
2. Démontrer de manière algébrique la conjecture émise.
2. Démontrer de manière algébrique la conjecture émise.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58
[Raisonner.]
On considère les fonctions f et g définies sur \mathbb { R } par f ( x ) = 3 x ^ { 2 } - x et g ( x ) = \dfrac { 2 } { 3 } x. On note respectivement C_f et C_g les courbes représentatives des fonctions f et g dans un repère orthonormé.
1. a. Tracer, à l'aide d'une calculatrice ou de GeoGebra, les courbes représentatives des fonctions f et g, notées respectivement C_f et C_g.
GeoGebra
b. Conjecturer alors les coordonnées des éventuels
points d'intersection des courbes C_f et C_g.
2. Démontrer de manière algébrique la conjecture émise.
2. Démontrer de manière algébrique la conjecture émise.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
[Chercher.]
f est une fonction polynôme du second degré.
- On donne les informations suivantes :
- Les antécédents de 0 par f sont -2 et 3.
- L'image de 4 par f est -5 .
Déterminer une expression de f en fonction de x .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
[Calculer.]
f est la fonction définie sur \mathbb { R } par f ( x ) = 5 x ^ { 2 } + 2 x - \sqrt { 7 }. On admet que l'équation f(x) = 0 a deux solutions, une positive \lambda et une négative \mu. L'objectif est de trouver un encadrement d'amplitude
0\text{,}001 de \lambda et \mu. À l'aide d'une calculatrice :
1. a. Tracer la représentation graphique de f .
GeoGebra
b. Déterminer deux entiers consécutifs encadrants \lambda.
2. a. Compléter le tableau de valeurs de f avec un pas de 0\text{,}1 sur l'intervalle formé par les deux entiers de la question précédente.
b. En déduire un encadrement d'amplitude 0\text{,}1 de \lambda.
c. Recommencer jusqu'à obtenir un encadrement d'amplitude 0\text{,}001.
3. Déterminer un encadrement d'amplitude 0\text{,}001 de \mu.
2. a. Compléter le tableau de valeurs de f avec un pas de 0\text{,}1 sur l'intervalle formé par les deux entiers de la question précédente.
| x | |||||||
| f(x) |
b. En déduire un encadrement d'amplitude 0\text{,}1 de \lambda.
c. Recommencer jusqu'à obtenir un encadrement d'amplitude 0\text{,}001.
3. Déterminer un encadrement d'amplitude 0\text{,}001 de \mu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
[Chercher.]
f est la fonction définie sur \mathbb { R } par f ( x ) = \dfrac { 1 } { 7 } x ^ { 2 } - \sqrt { 5 } x + 3. On admet que l'équation f(x) = 0 admet deux solutions.
À l'aide de la calculatrice, déterminer une valeur approchée à 10 ^ { - 3 } près de chacune d'elles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
[Chercher.]
f est une fonction polynôme du second degré. Sans essayer de trouver l'expression de f , compléter le tableau de valeurs suivant.
| x | -5 | -1 | 2 | |
| f(x) | 66 | 18 | 4,56 | 3 |
| x | 4 | 4,6 | 7 | 11 |
| f(x) | 3 | 4,56 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
[Chercher.]
Voici la courbe représentative \text{C}, dans un repère orthogonal, d'une fonction polynôme du second degré f définie sur \mathbb { R } par les expressions suivantes :
- f ( x ) = a x ^ { 2 } + b x + c : forme développée ;
- f ( x ) = a \left( x - x _ { 1 } \right) \left( x - x _ { 2 } \right) : forme factorisée ;
- f ( x ) = a ( x - \alpha ) ^ { 2 } + \beta : forme canonique.
Le zoom est accessible dans la version Premium.
1. Répondre aux questions suivantes par lecture graphique.
a. Quel est le signe de a ?
b. Donner les valeurs de c , x _ { 1 } , x _ { 2 } , \alpha et \beta.
2. En déduire la valeur de a .
a. Quel est le signe de a ?
b. Donner les valeurs de c , x _ { 1 } , x _ { 2 } , \alpha et \beta.
2. En déduire la valeur de a .
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah