Approximation des racines par la méthode de Héron

D’après le mathématicien Héron d’Alexandrie, déterminer $\sqrt { m }$ revient à tracer un carré d’aire égale à $m.$ Étudions le cas $m = 2 .$ Dans l’ensemble de cette méthode les points ont des coordonnées positives.

1. Lancer GeoGebra et placer les points $\text{O} ( 0 \: ; 0 )$ et $\mathrm { A } _ { 1 } ( m \: ; 0 ).$ Tracer le rectangle $\mathrm { O } \mathrm { A } _ { 1 } \mathrm { B } _ { 1 } \mathrm { C } _ { 1 }$ d’aire $m.$

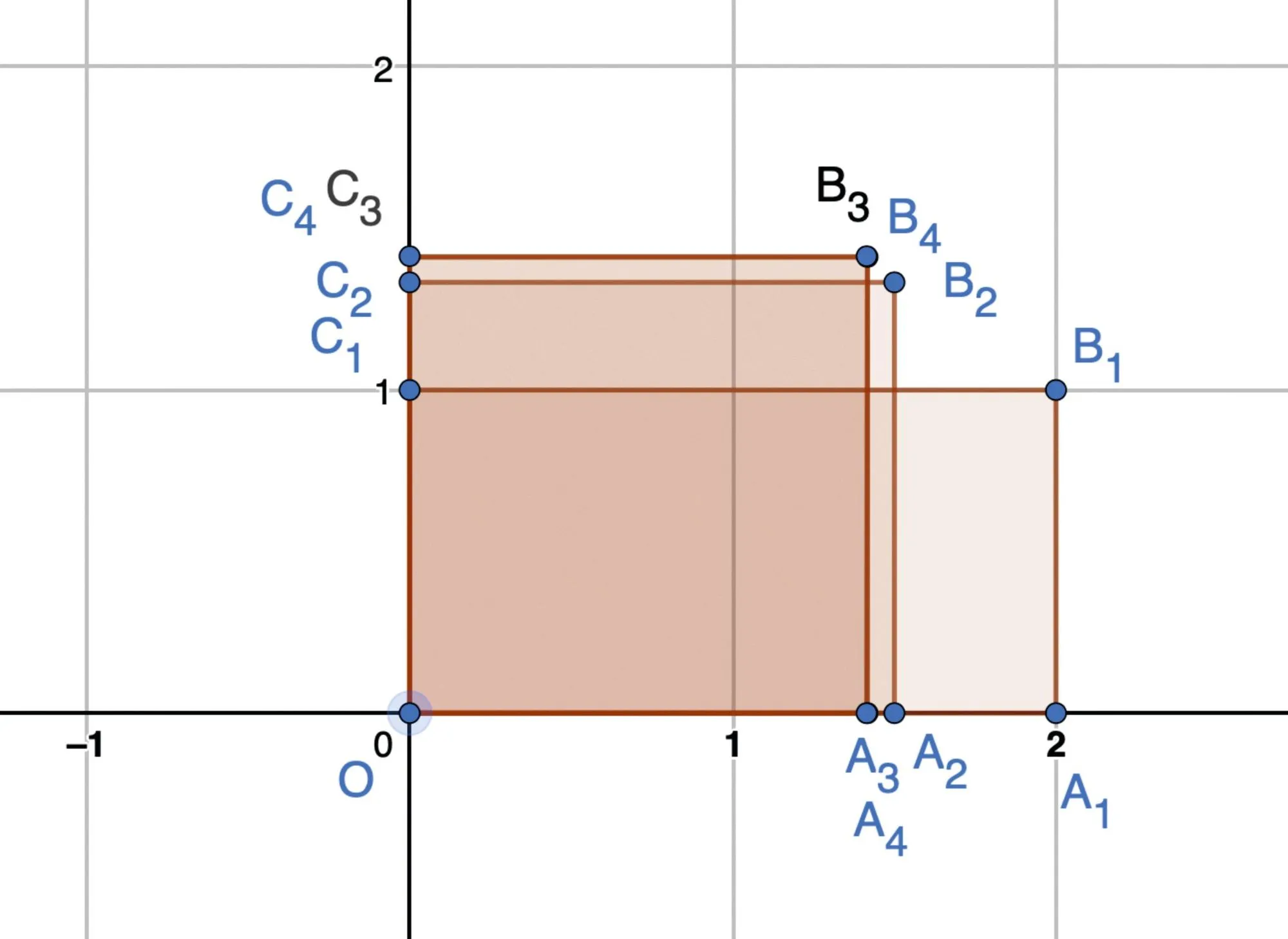
2. a. Placer $\text{A}_{2}$ d’ordonnée $0$ et d’abscisse $\dfrac { x _ { \mathrm { B } _ { 1 } } + y _ { \mathrm { B } _ { 1 } } } { 2 }.$
b. Calculer la longueur $\mathrm { A } _ { 2 } \mathrm { B } _ { 2 }$ pour que le rectangle $\mathrm { OA } _ { 2 } \mathrm { B } _ { 2 } \mathrm { C } _ { 2 }$ soit d’aire $m.$ Quelles sont les coordonnées de $\text{B}_{2} \: ?$

3. a. Recommencer cette opération jusqu’à la construction de $\text{B}_{4}.$
On commencera par calculer l’abscisse de $\text{A}_{3} \: :$ $\dfrac { x _ { \mathrm { B } _ { 2 } } + y _ { \mathrm { B } _ { 2 } } } { 2 }$

b. Que remarque-t-on sur les coordonnées de $\mathrm { B } _ { k } ?$

c. En déduire une valeur approchée de $\sqrt { 2 }.$

4. a. En utilisant cette méthode, déterminer une valeur approchée de $\sqrt { 5 }.$

b. En déduire des approximations des solutions de $- 2 ( x + 3 ) ^ { 2 } + 10 = 0.$

Lancer le module Geogebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

Soit $n$ un entier naturel non nul. On considère l’algorithme de Héron suivant.

Étape 1 : $x _ { 0 } = m$ et $x _ { 1 } = \dfrac { x _ { 0 } + \dfrac { m } { x _ { 0 } } } { 2 }$

Étape 2 : $x _ { 2 } = \dfrac { x _ { 1 } + \dfrac { m } { x _ { 1 } } } { 2 }$

Étape 3 : $x _ { 3 } = \dfrac { x _ { 2 } + \dfrac { m } { x _ { 2 } } } { 2 }$
...
Étape $n$ : $x _ { n } = \dfrac { x _ { n - 1 } + \dfrac { m } { x _ { n - 1 } } } { 2 }$

1. Compléter l’algorithme suivant afin d’obtenir l’affichage de $x_ { n }$ pour $n$ et $m$ donnés.

$\boxed{ \begin{array} { l } \text {Fonction Heron}(m, n) \\ \quad \text {X } \leftarrow m \\ \quad \quad \text {Pour } k \text { allant de ... à ... } \\ \quad \quad \quad \text {X } \leftarrow \text {...} \\ \quad \quad \text {Fin Pour} \\ \quad \text {Retourner X} \\ \text {Fin Fonction} \end{array} }$

2. a. Expliquer les lignes de cet algorithme.

b. Modifier cet algorithme pour que l’ensemble des valeurs $x_{k}$ pour $k$ allant de $1$ à $n$ soient affichées.

3. a. Programmer cet algorithme avec Python et le tester pour $m = 2$ et $n = 4 .$
b. Qu’observe-t-on sur les différentes valeurs affichées ?

c. En déduire une valeur approchée de $\sqrt { 2 }.$

4. a. En utilisant cet algorithme, déterminer une valeur approchée de $\sqrt { 5 }.$

b. En déduire des approximations des solutions de $- 2 ( x + 3 ) ^ { 2 } + 10 = 0.$