Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 2
Entraînement 1
Fonction valeur absolue
9 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39
[Calculer.]
Sans utiliser la calculatrice, exprimer les nombres suivants sans le symbole valeur absolue.
1. | 3 - 5 |
2. \left| 2 - \dfrac { 3 } { 7 } \right|
3. | \pi - 1 |
4. | 4 - \sqrt { 23 } |
5. \left| \dfrac { 1 - \sqrt { 2 } } { \sqrt { 5 } - 2 } \right|
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40
[Raisonner.] f est la fonction définie sur \mathbb { R } par f ( x ) = 5 - 3 | x |. 1. Étudier la parité de f .
2. En déduire une interprétation graphique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41
[Raisonner.]
Dans chaque cas, préciser en justifiant si l'affirmation est vraie ou fausse. Dans le cas où l'affirmation est fausse, la rectifier pour qu'elle soit vraie. 1. L'image de \sqrt { 6 } - 3 par la fonction valeur absolue est 3 - \sqrt { 6 }.
2. L'image de 5 par la fonction valeur absolue est -5 .
3. Si | x | \lt 3 , alors x \in ] - 3 \: ; 3 [.
4. Pour tout réel x , on a : \sqrt { x ^ { 2 } } = x.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42
[Calculer.]
Résoudre les inéquations suivantes.
1. | x | \lt 2
2. 3 \leqslant | x | \leqslant 4
2. 3 \leqslant | x | \leqslant 4
3. | x - 3 | \leqslant 5
4. | x + 4 | > 5
4. | x + 4 | > 5
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43
Algo
[Calculer.]
On considère un réel k quelconque. Voici un algorithme incomplet permettant d'obtenir les
solutions éventuelles de l'équation | x | = k :
\boxed{
\begin{array} { l } { \text {Définir Solution } (k) \text { : } } \\
\quad \text {Si } k \lt 0 \text { alors : } \\
\quad \quad\text{Retourner « … solution » } \\
\quad \text {Sinon } \\
\quad \quad \text {Si ... alors : } \\
\quad \quad \quad \text {Retourner } 0 \\
\quad \quad \text {Sinon } m \leftarrow \text {...} \\
\quad \quad \quad n \leftarrow \text {...} \\
\quad \quad \quad \text {Retourner } m \text { et } n\\
\quad \quad \text {Fin Si} \\
\quad \text {Fin Si} \\
\end{array}
}
1. Recopier et compléter l'algorithme.
2. a. Programmer cet algorithme à l'aide de la calculatrice ou d'un ordinateur.
b. Tester l'algorithme avec : k = 4 , k = 0 et k = -3 .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44
Démo
[Raisonner.]
Soit a \geqslant 0. On se propose de trouver une condition nécessaire et suffisante sur le réel x pour que | x | \leqslant a \:\: ( \mathrm { I } ). 1. Résoudre l'inéquation ( \mathrm { I } ) sur [ 0 \: ; + \infty [.
2. Résoudre l'inéquation ( \mathrm { I } ) sur ] - \infty \: ; 0 ].
3. Conclure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45
[Représenter.]
1. À partir de la représentation de la fonction valeur absolue faite à la calculatrice, résoudre :
Le zoom est accessible dans la version Premium.
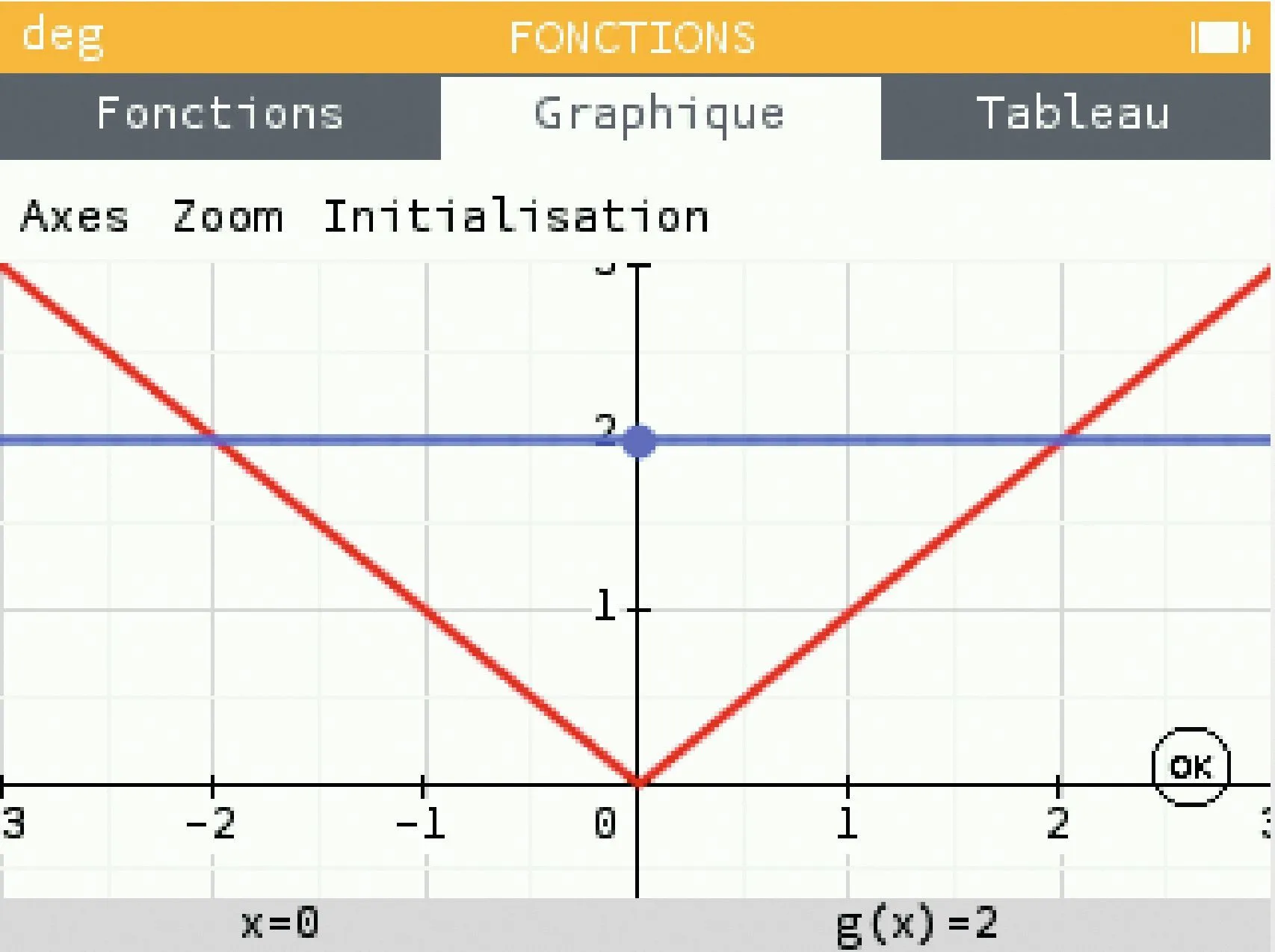
a. | x | = 2
b. | x | \lt 2
c.| x | \gt 2
2. En déduire alors la résolution de l'inéquation | x + 4 | \geqslant 2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46
[Raisonner.]
x est un réel tel que 2 \lt x \leqslant 5. Déterminer un encadrement des expressions suivantes. 1. | x |
2. 3 | x |
3. | x | - 1
4. 4 | x |+2
5. 1-5 | x |
6. 4-| x -2|
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47
[Raisonner.]
Reprendre l'exercice précédent pour x vérifiant les conditions suivantes. 1. - 4 \leqslant x \leqslant - 3
2. - 5 \lt x \leqslant 3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
[Calculer.] Dans chaque cas, donner un encadrement de | x |. On pourra éventuellement se référer à la courbe représentative de la fonction valeur absolue. 1. - 3 \leqslant x \lt - 2
2. 5 \leqslant x \leqslant 7
3. - \pi \lt x \lt 2 \pi
4. - 3 \lt x \leqslant 2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
Démo
[Raisonner.]
Soit f la fonction définie sur \mathbb { R } par f ( x ) = \sqrt { x ^ { 2 } }. 1. Justifier que f est définie sur \mathcal { D } _ { f } = \mathbb { R }.
2. Déterminer l'image par f de quatre nombres réels appartenant à l'intervalle [ - 10 ; 10 ] en prenant soin de ne pas choisir que des nombres de même signe.
3. Que peut-on conjecturer ? Démontrer cette conjecture.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
[Raisonner.]
Le but de l'exercice est d'établir un lien entre | x | \times | y | et | x y |, pour tous réels x et y.
1. a. Choisir deux réels x et y quelconques.
b. Calculer | x | \times | y | et | x y |.
c. Reproduire l'opération plusieurs fois pour établir une conjecture.
b. Calculer | x | \times | y | et | x y |.
c. Reproduire l'opération plusieurs fois pour établir une conjecture.
2. x et y sont maintenant des réels quelconques. Montrer la conjecture dans les quatre cas suivants.
a. x = 0 ou y = 0
b. x \lt 0 et y \lt 0
c. x \lt 0 et y \gt 0
d. x \gt 0 et y \gt 0
3. Conclure.
a. x = 0 ou y = 0
b. x \lt 0 et y \lt 0
c. x \lt 0 et y \gt 0
d. x \gt 0 et y \gt 0
3. Conclure.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah