Chapitre 2
Entraînement 3
Étude des fonctions polynômes du second degré
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
[Chercher.] Pour chaque cas, donner un encadrement de x^2 , ou une inégalité vérifiée par x^2 .
1. - 2 \lt x \leqslant 7
2. 4 \leqslant x \lt 7
3. x \gt - 3
2. 4 \leqslant x \lt 7
3. x \gt - 3
4. x \lt - 2
5. - 6 \leqslant x \lt 3
6. - 11 \lt x \leqslant - 2
5. - 6 \leqslant x \lt 3
6. - 11 \lt x \leqslant - 2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
[Raisonner.] x est un réel tel que - 4 \lt x \leqslant 3. Déterminer un encadrement de :
1. ( x + 5 ) ^ { 2 } - 1
2. - 3 ( x - 4 ) ^ { 2 } + 6
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
66
[Chercher.]
Résoudre dans \mathbb { R } les inéquations suivantes.
1. ( x - 3 ) ^ { 2 } \leqslant 36
2. 3 ( x + 1 ) ^ { 2 } - 8 \leqslant 4
2. 3 ( x + 1 ) ^ { 2 } - 8 \leqslant 4
3. 2 ( x + 1 ) ^ { 2 } - 4 \geqslant 10
4. - 5 ( x - 2 ) ^ { 2 } \geqslant 10
4. - 5 ( x - 2 ) ^ { 2 } \geqslant 10
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
67
[Chercher.] f est une fonction polynôme du second degré définie par f(x) = ax^2 + bx + c . On note C_f sa courbe représentative dans un repère orthonormé.
On donne les informations suivantes :
- Le point de C_f d'abscisse 0 a pour ordonnée -2 .
- f est d'abord croissante puis décroissante.
- Les antécédents de -2 par f sont 0 et 5.
Proposer deux expressions possibles de f en fonction de x .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
68
DÉMO
[Raisonner.]
f est la fonction définie sur \mathbb { R } par f ( x ) = 5 x ^ { 2 } - 3.
L'objectif de cet exercice est de démontrer que f est décroissante sur ] - \infty \: ; 0 ] puis de dresser son tableau de variations sur \mathbb { R }. 1. Compléter la démonstration suivante :
« On considère deux réels a et b tels que : a \lt b \leqslant
Alors : a^2
5a^2
5a^2 - 3
f(a)
Donc, la fonction f est
2. Dresser le tableau de variations de f sur \mathbb { R }.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
69
[Raisonner.]
f est la fonction définie sur \mathbb { R } par f(x) = -4x^2 + 1 . 1. Démontrer que f est croissante sur ] - \infty \: ; 0 ].
2. Dresser son tableau de variations sur \mathbb { R }.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
70
DÉMO
[Raisonner.] f est la fonction définie sur \mathbb { R } par f ( x ) = 4 ( x + 2 ) ^ { 2 } - 3.
L'objectif de cet exercice est de démontrer que f est décroissante sur ] - \infty \: ; -2 ] puis de dresser son tableau de variations sur \mathbb { R }. 1. Compléter la démonstration suivante :
« On considère deux réels a et b tels que : a \lt b \leqslant
Alors : a + 2
( a + 2 ) ^ { 2 }
4 ( a + 2 ) ^ { 2 }
4 ( a + 2 ) ^ { 2 }-3
f(a)
Donc, la fonction f est
2. Dresser le tableau de variations de f sur \mathbb { R }.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
71
[Raisonner.] f est la fonction définie sur \mathbb { R } par f ( x ) = - 2 ( x + 7 ) ^ { 2 } - 1 . C_f est la représentation graphique de f dans un repère orthonormal du plan. 1. a. Démontrer que la fonction f est croissante sur ] - \infty \: ; - 7 ].
b. Dresser son tableau de variations sur \mathbb { R }.
Cliquez pour accéder à une zone de dessin
2. Donner l'équation réduite de l'axe de symétrie de C_f et les coordonnées du sommet \text{S} de C_f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
72
DÉMO
[Raisonner.] f est la fonction définie sur \mathbb { R } par f ( x ) = - ( x + 3 ) ^ { 2 } + 5.
L'objectif de cet exercice est de démontrer que f admet un maximum sur \mathbb { R }.
Compléter la démonstration suivante :
« Pour tout réel x , on a :
( x + 3 ) ^ { 2 }
-( x + 3 ) ^ { 2 }
-( x + 3 ) ^ { 2 }+5
f(x)
De plus : f (
Donc, la fonction f admet
Il est atteint pour x =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
73
[Raisonner.]
f est la fonction définie sur \mathbb { R } par {f ( x ) = 6 ( x - 2 ) ^ { 2 } - 7.}
Déterminer l'extremum de f sur \mathbb { R }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
74
[Raisonner.]
g est la fonction définie sur \mathbb { R } par {g ( x ) = - 3 ( x + 4 ) ^ { 2 } - 2.}
Déterminer l'extremum de g sur \mathbb { R }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
75
DÉMO
[Raisonner.] f est la fonction définie sur \mathbb { R } par f ( x ) = 5 ( x - 1 ) ^ { 2 } - 3. C_f est la représentation graphique de f dans un repère orthonormé du plan. 1. Démontrer que f est décroissante sur ] - \infty \: ; 1 ].
2. Dresser le tableau de variations de f sur \mathbb { R }.
Cliquez pour accéder à une zone de dessin
3. Déterminer l'extremum de f sur \mathbb { R }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
76
[Représenter.]
f est une fonction polynôme définie sur \mathbb { R } par f(x) = ax^2 + bx + c dont voici le tableau de signes.


Dans chaque cas, préciser si l'affirmation est vraie ou fausse. Justifier chacune de vos réponses. Dans le cas où l'affirmation est fausse, la rectifier pour que celle-ci soit vraie.
1. f ( - 10 ) \lt 0
2. f ( - 9 ) \geqslant f ( 1 )
3. f(0) = 2
2. f ( - 9 ) \geqslant f ( 1 )
3. f(0) = 2
4. a \lt 0
5. L'ensemble des solutions de l'équation f ( x ) = 0 est \mathrm { S } = \{ - 8 \: ; 2 \}.
6. L'ensemble des solutions de l'inéquation f ( x ) \lt 0 est \mathrm { S } = [ - 8 \: ; 2 ].
5. L'ensemble des solutions de l'équation f ( x ) = 0 est \mathrm { S } = \{ - 8 \: ; 2 \}.
6. L'ensemble des solutions de l'inéquation f ( x ) \lt 0 est \mathrm { S } = [ - 8 \: ; 2 ].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
77
[Représenter.]
f est définie sur \mathbb { R } par : f ( x ) = 2 ( x - 3 ) ^ { 2 } - 8 = 2 ( x - 5 ) ( x - 1 ). \mathcal { P } est sa représentation graphique dans un repère orthonormé. 1. Déterminer la forme développée de f .
2. Sans démonstration et en précisant la forme utilisée,
donner :
a. l'axe de symétrie et le sommet de \mathcal { P } ;
b. le signe de f .
a. l'axe de symétrie et le sommet de \mathcal { P } ;
b. le signe de f .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
78
[Représenter.] f est une fonction polynôme du second degré dont on a tracé la représentation graphique à l'aide de la calculatrice.

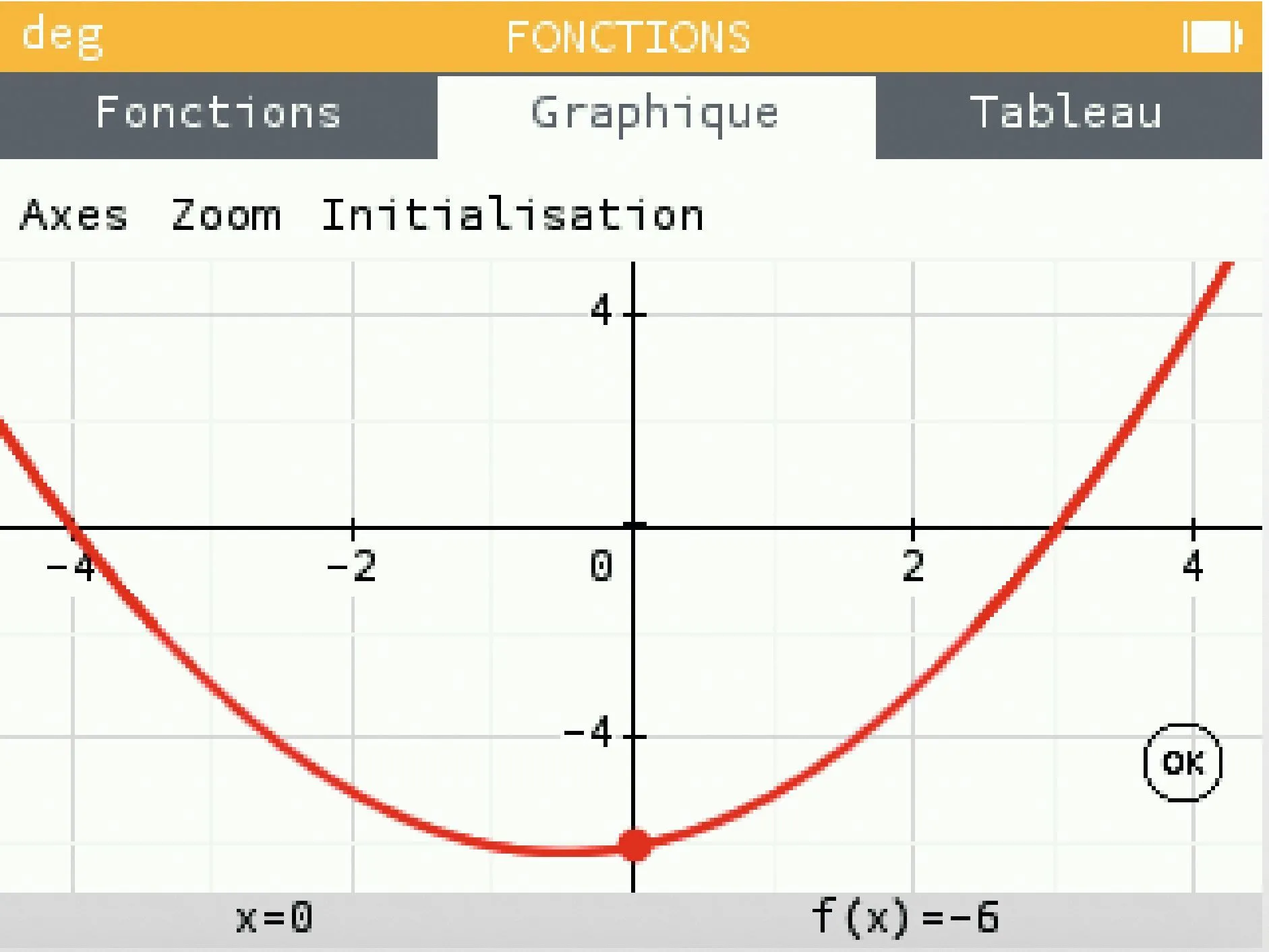
1. Dresser le tableau de signe de f sur \mathbb { R }.
Cliquez pour accéder à une zone de dessin
2. Déterminer la forme factorisée de f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
79
[Chercher.]
f est une fonction polynôme du second degré dont on donne les informations suivantes :
- l'ensemble des solutions de l'inéquation f ( x ) \geqslant 0 est ] - \infty \: ; 1 ] \cup [ 2 \: ; + \infty [ \: ;
- l'image de 0 par f est 3.
Déterminer une expression de la fonction f en fonction de x .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
80
[Chercher.]
f est une fonction polynôme du second degré dont voici le tableau de signes.


Proposer une expression de f en fonction de x .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
81
[Chercher.] f est la fonction définie sur \mathbb { R } par f ( x ) = 5 ( x - 2 ) ( x + 5 ) 1. Étudier le signe de f sur \mathbb { R }.
2. En déduire l'ensemble des solutions de :
a. f ( x ) = 0
b. f ( x ) \leqslant 0
c. f ( x ) \gt 0
a. f ( x ) = 0
b. f ( x ) \leqslant 0
c. f ( x ) \gt 0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
82
[Chercher.] Résoudre dans \mathbb { R } les inéquations suivantes. 1. 5 ( x + 2 ) ( x - 6 ) \lt 0
2. - ( x - 5 ) ( x + 11 ) \geqslant 0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
83
[Chercher.]
f est la fonction définie sur \mathbb { R } par : {f ( x ) = 6 ( x - 3 ) ( x + 4 ).} C_f est la représentation graphique de f dans un repère orthonormal du plan. 1. Déterminer les antécédents de 0 par f .
2. Déterminer l'ensemble des abscisses des points de C_f situés au-dessus de l'axe des abscisses.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
84
[Raisonner.] On considère les fonctions f et g définies sur \mathbb { R } par f ( x ) = x ^ { 2 } et g ( x ) = 6 x - 9.
1. a. Tracer, à l'aide de GeoGebra ou d'une calculatrice, les courbes représentatives des fonctions f et g , notées respectivement C_f et C_g .
b. Conjecturer alors les coordonnées du ou des points
d'intersection des courbes C_f et C_g .
c. Conjecturer la position relative des courbes C_f et C_g .
2. Démontrer de manière algébrique les deux conjectures émises.
c. Conjecturer la position relative des courbes C_f et C_g .
2. Démontrer de manière algébrique les deux conjectures émises.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
85
[Raisonner.] On considère les fonctions f et g définies sur \mathbb { R } par f ( x ) = x ^ { 2 } et g ( x ) = - 2 x ^ { 2 } + 5 x + 2.
1. a. Tracer, à l'aide de GeoGebra ou d'une calculatrice, les courbes représentatives des fonctions f et g , notées respectivement C_f et C_g .
b. Conjecturer les coordonnées des points d'intersection des courbes C_f et C_g .
b. Conjecturer les coordonnées des points d'intersection des courbes C_f et C_g .
c. Conjecturer la position relative des courbes C_f et C_g .
2. Justifier que pour tout réel x , on a : f ( x ) - g ( x ) = ( 3 x + 1 ) ( x - 2 ).
3. Démontrer les conjectures émises.
2. Justifier que pour tout réel x , on a : f ( x ) - g ( x ) = ( 3 x + 1 ) ( x - 2 ).
3. Démontrer les conjectures émises.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
86
DÉMO
[Raisonner.] f est la fonction définie sur \mathbb { R } par f ( x ) = 3 ( x - 1 ) \left( x - \dfrac { 7 } { 3 } \right).
C_f est la représentation graphique de f dans un repère orthonormé du plan.
1. Montrer que, pour tout réel x , on a :
a. f ( x ) = 3 x ^ { 2 } - 10 x + 7
b. f ( x ) = 3 \left( x - \dfrac { 5 } { 3 } \right) ^ { 2 } - \dfrac { 4 } { 3 }
a. f ( x ) = 3 x ^ { 2 } - 10 x + 7
b. f ( x ) = 3 \left( x - \dfrac { 5 } { 3 } \right) ^ { 2 } - \dfrac { 4 } { 3 }
2. Dans chacun des cas suivants, indiquer la forme la plus adaptée et résoudre les inéquations :
a. f ( x ) \leqslant 0
b. f ( x ) \gt 7
c. f ( x ) \leqslant 6
a. f ( x ) \leqslant 0
b. f ( x ) \gt 7
c. f ( x ) \leqslant 6
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
87
[Raisonner.]
f est la fonction définie sur \mathbb { R } par f ( x ) = - \left( x - \dfrac { 13 } { 2 } \right) \left( x - \dfrac { 1 } { 2 } \right).
C_f est la représentation graphique de f dans un repère orthonormal du plan.
À l'aide de l'outil calcul formel de GeoGebra, nous obtenons les résultats suivants.
C_f est la représentation graphique de f dans un repère orthonormal du plan.
À l'aide de l'outil calcul formel de GeoGebra, nous obtenons les résultats suivants.

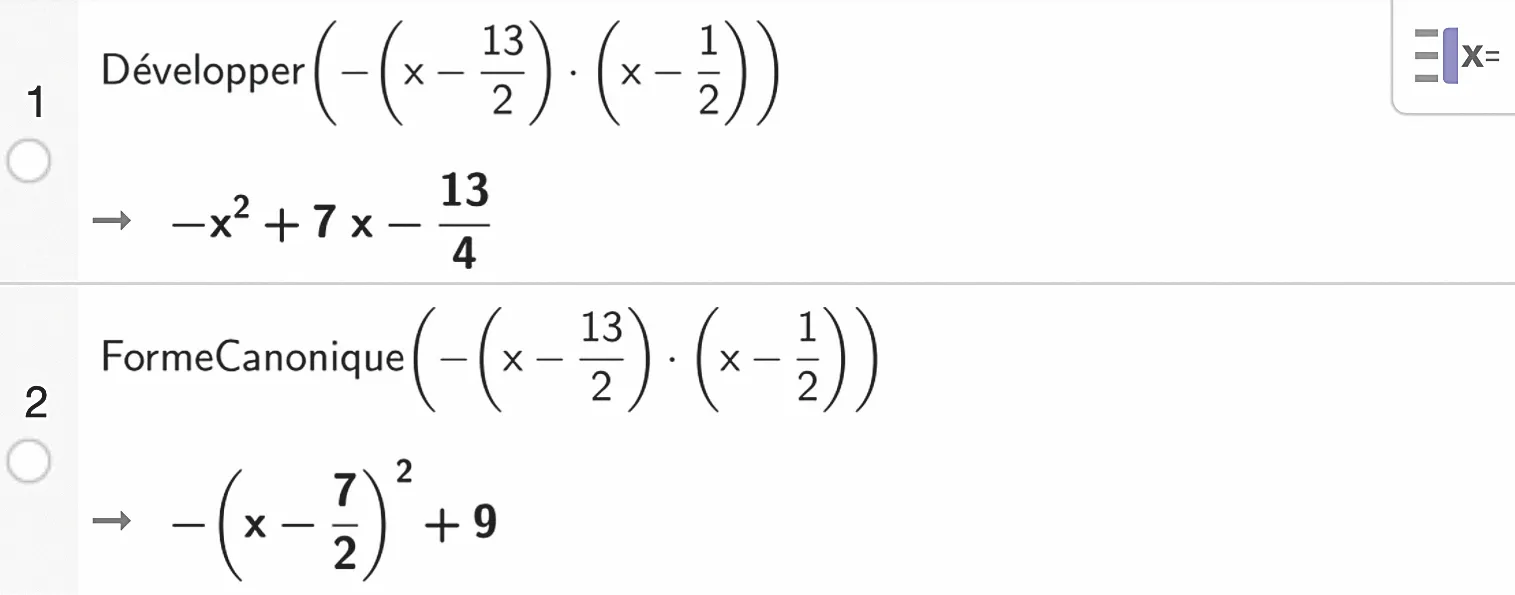
Dans chacun des cas suivants, indiquer la forme la plus
adaptée et effectuer la tâche demandée.
1. Calculer f(0).
2. Résoudre l'équation f(x) = 9 .
3. Dresser le tableau de signes de f .
2. Résoudre l'équation f(x) = 9 .
3. Dresser le tableau de signes de f .
Cliquez pour accéder à une zone de dessin
4. Résoudre l'inéquation f(x) \gt 0 .
5. Déterminer l'ensemble des abscisses des points de C_f se situant en dessous de l'axe des abscisses.
5. Déterminer l'ensemble des abscisses des points de C_f se situant en dessous de l'axe des abscisses.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
88
DÉMO
[Raisonner.] f est la fonction définie sur \mathbb { R } par f ( x ) = - 3 ( x + 2 ) ^ { 2 } + 27. C_f est la représentation graphique de f dans un repère orthonormal du plan.
1. Montrer que, pour tout réel x , on a :
a. f ( x ) = - 3 x ^ { 2 } - 12 x + 15 ;
b. f ( x ) = - 3 ( x - 1 ) ( x + 5 ).
2. Dans chacun des cas suivants, indiquer la forme la plus adaptée et effectuer la tâche demandée.
a. Déterminer les antécédents de 0 par f .
b. Calculer f(-2) .
a. f ( x ) = - 3 x ^ { 2 } - 12 x + 15 ;
b. f ( x ) = - 3 ( x - 1 ) ( x + 5 ).
2. Dans chacun des cas suivants, indiquer la forme la plus adaptée et effectuer la tâche demandée.
a. Déterminer les antécédents de 0 par f .
b. Calculer f(-2) .
c. Déterminer l'extremum de f sur \mathbb { R }.
d. Résoudre l'équation f ( x ) = 15.
e. Déterminer les coordonnées du point d'intersection de C_f avec l'axe des ordonnées.
d. Résoudre l'équation f ( x ) = 15.
e. Déterminer les coordonnées du point d'intersection de C_f avec l'axe des ordonnées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
89
[Chercher.]
Francis, entrepreneur, décide de fabriquer une gouttière dont la section a une forme parabolique.



La fonction polynôme du second degré f qui servira à la conception est représentée ci-dessus. Pour lancer la fabrication, Francis doit déterminer une expression de la fonction f . Hélas, il a perdu la plupart de ses documents de préparation.
Il connaît seulement deux informations :
- L'ensemble des solutions de f ( x ) \leqslant 0 est un intervalle d'amplitude 10 ;
- Le sommet de la parabole représentant f est le point S ( - 3 \: ; - 5 ).
Aider Fabrice à retrouver une expression de f pour lancer la production.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
90
[Chercher.]
À l'aide de la calculatrice, on a tracé la représentation graphique d'une fonction polynôme du second degré g. Le sommet de la parabole est le point de coordonnées \left( - \dfrac { 1 } { 2 } \: ; - \dfrac { 25 } { 12 } \right).
De plus, la courbe coupe l'axe des ordonnées au point de coordonnées (0 \: ; - 2) .

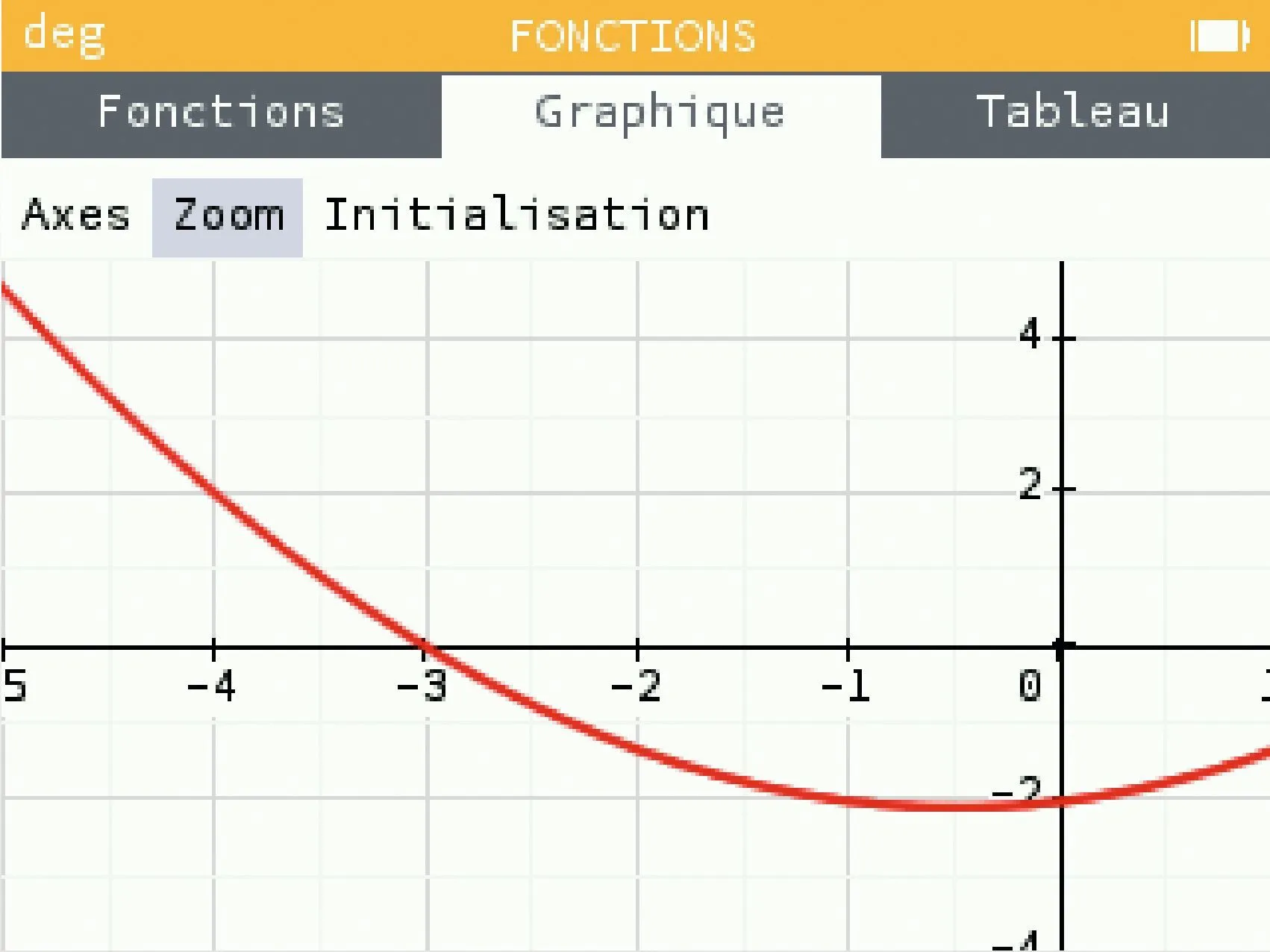
En le justifiant, déterminer les deux solutions de l'équation g(x) = 0 .
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

