Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 2
TP / TICE 1
Approcher l'aire sous une courbe par la méthode des rectangles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
f est définie sur [ 0 \: ; 1 ] par f(x) = x^2. On note \mathcal { P } sa représentation graphique. \mathcal { D } est l'aire du domaine hachuré en rouge.
On subdivise l'intervalle [ 0 \: ; 1 ] en n intervalles de la forme \left[ \dfrac { k } { n } \: ; \dfrac { k + 1 } { n } \right],
où n et k sont des entiers tels que 1 \leqslant n \leqslant 20 et 0 \leqslant k \leqslant n - 1.
On note \text{A}_{k} l'aire de chaque rectangle bleu de la figure.
\mathcal { P } coupe chaque rectangle au milieu de la largeur. On note \mathrm { I } = \mathrm { A } _ { 0 } + \mathrm { A } _ { 1 } + \ldots + \mathrm { A } _ { n - 1 }.
La méthode des rectangles montre que \text{I} est une valeur approchée de \mathcal { D }.
On note \text{A}_{k} l'aire de chaque rectangle bleu de la figure.
\mathcal { P } coupe chaque rectangle au milieu de la largeur. On note \mathrm { I } = \mathrm { A } _ { 0 } + \mathrm { A } _ { 1 } + \ldots + \mathrm { A } _ { n - 1 }.
La méthode des rectangles montre que \text{I} est une valeur approchée de \mathcal { D }.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Question préliminaire
En utilisant le graphique, exprimer \text{A}_{k} en fonction de k .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
On souhaite approcher \mathcal { D } en calculant \text{I} à l'aide d'une des trois méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1GeoGebra
Avec GeoGebra, tracer la courbe \mathcal { P } en utilisant la
saisie : f(x) = \text{Si} (0 \lt x \lt 1, x ^ 2).
1. a. Faire une construction pour n = 3 .
b. Déterminer une valeur approchée de \mathcal{D} .
2. On souhaite désormais obtenir un encadrement plus précis de \mathcal{D} en faisant varier la valeur de n .
a. Créer un curseur n variant de 0 à 20 avec un pas de 1.
b. Définir le nombre \text{I} par : \text{I}=\text{SommeRectangles}(x^2 , 0 ,1, n,1/2).
c. En déduire une valeur approchée de \mathcal{D} pour n = 20 .
2. On souhaite désormais obtenir un encadrement plus précis de \mathcal{D} en faisant varier la valeur de n .
a. Créer un curseur n variant de 0 à 20 avec un pas de 1.
b. Définir le nombre \text{I} par : \text{I}=\text{SommeRectangles}(x^2 , 0 ,1, n,1/2).
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
n est un entier naturel non nul. On considère l'algorithme suivant :
\boxed{
\begin{array} { l } { \text { Fonction Aire} (n) \text { : } } \\
\quad \text { I } \leftarrow \dfrac { 1 } { n } \times \left( \dfrac { 1 } { 2 n } \right) ^ { 2 } \\
\quad \quad \text { Pour } k \text { allant de ... à ... } \\
\quad \quad \quad \text {I} \leftarrow \text {...} \\
\quad \quad \text {Fin Pour} \\
\quad \text {Retourner I}\\
\text {Fin Fonction} \\
\end{array}
}
1. Exprimer \text{A}_{0} en fonction de n .
2. Expliquer la ligne 2 de cet algorithme.
3. Compléter cet algorithme afin d'obtenir \text{I} pour un entier naturel n donné.
4. Programmer et tester cet algorithme avec Python et en déduire une valeur approchée de \mathcal{D} pour n = 20 .
2. Expliquer la ligne 2 de cet algorithme.
3. Compléter cet algorithme afin d'obtenir \text{I} pour un entier naturel n donné.
4. Programmer et tester cet algorithme avec Python et en déduire une valeur approchée de \mathcal{D} pour n = 20 .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 3Tableur
Ouvrir une feuille de calcul et recopier la feuille suivante.
Le zoom est accessible dans la version Premium.
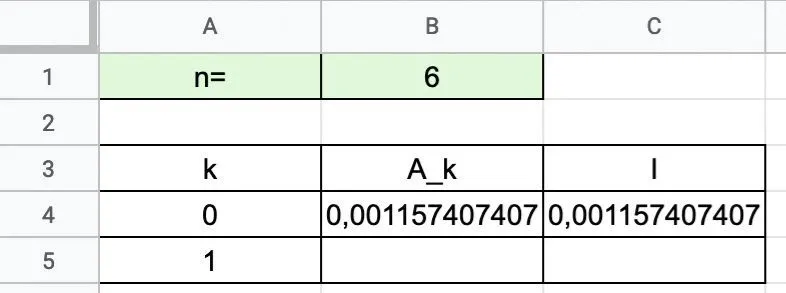
1. a. Calculer \text{A}_{0} pour n = 6 .
b. Comment calculer la valeur obtenue en B4.
c. Quelle formule faut-il écrire en B5 pour obtenir \text{A}_{1} ?
d. Jusqu'à quelle ligne doit-on étirer la formule pour obtenir toutes les valeurs de \text{A}_{k} pour n = 6 ?
Aide : On pensera à utiliser les symboles \$ si nécessaire.
2. a. En C5, on a saisi = \text{C}4 + \text{B}5. Expliquer la formule.
b. En déduire une valeur approchée de \mathcal {D}.
b. Comment calculer la valeur obtenue en B4.
c. Quelle formule faut-il écrire en B5 pour obtenir \text{A}_{1} ?
d. Jusqu'à quelle ligne doit-on étirer la formule pour obtenir toutes les valeurs de \text{A}_{k} pour n = 6 ?
Aide : On pensera à utiliser les symboles \$ si nécessaire.
2. a. En C5, on a saisi = \text{C}4 + \text{B}5. Expliquer la formule.
b. En déduire une valeur approchée de \mathcal {D}.
3. Modifier la feuille de calcul pour obtenir une valeur approchée de \mathcal {D} pour n = 20 .
GeoGebra
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah