Sommaire

Mes pages

ouverture

p. 1-11

Nombres et calculs

Fonctions

Ch. 1

Généralités sur les fonctions

Ch. 2

Variations de fonctions

Ch. 3

Fonctions affines

Ch. 4

Fonctions de référence

Géométrie

Ch. 5

Repérage et configuration dans le plan

Ch. 6

Notion de vecteur

Ch. 7

Colinéarité de vecteurs

Ch. 8

Équations de droites

Statistiques et probabilités

Ch. 9

Informations chiffrées

Ch. 10

Statistiques descriptives

Ch. 11

Probabilités et échantillonnage

Annexes

Exercices transversaux

Cahier d'algorithmique et de programmation

Rappels de collège

Jeux de société

Nos dossiers d'actualité

Dossier d'actualité

Page précédente

Chapitre 0

Cours et exercices

Intervalles et valeur absolue

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Cours

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Définition

Soient a et b deux nombres réels.

On appelle intervalle fermé [a\,; b] l'ensemble des nombres réels x tels que a \leqslant x \leqslant b.
On appelle intervalle ouvert ]a\,; b[ l'ensemble des nombres réels x tels que a \lt x \lt b .
On définit de même les intervalles [a\,; b[ et ]a\,; b] .
On note [a\,; +\infty[ l'ensemble des nombres réels x tels que x \geqslant a .
On note ]a\,; +\infty[ l'ensemble des nombres réels x tels que x \gt a .
On définit de même ]-\infty \,; a] et ]-\infty \,; a[ .

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Notation

Le symbole +\infty se lit « plus l'infini ».
Le symbole -\infty se lit « moins l'infini ».

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Définition

Soient \text{I} et \text{J} deux intervalles.

L'intersection de \text{I} et \text{J} est l'ensemble des réels qui appartiennent à la fois à I et à J.
La réunion de \text{I} et \text{J} est l'ensemble des réels qui appartiennent à \text{I} ou à \text{J}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Notation

L'intersection de deux intervalles \text{I} et \text{J} se note \text{I} \cap \text{J}.
La réunion de deux intervalles \text{I} et \text{J} se note \text{I} \cup \text{J}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exemples

La réunion des intervalles [3\,; 7] et [4\,; 10] est l'intervalle [3\,; 10]. On note [3\,; 7] \cup [4\,; 10].
L'intersection des intervalles [3\,; 7] et [4\,; 10] est l'intervalle [4\,; 7] . On note [3\,; 7] \cap [4\,; 10] .

On peut représenter graphiquement un intervalle sur une droite graduée :

Intervalle	Représentation graphique
[-3\,;4]
]2\,;7[

On a dessiné des crochets au bord de l'intervalle pour indiquer s'il est ouvert ou fermé.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

EXCLU. PREMIUM 2023

Union et intersection d'intervalles

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Définition

On appelle valeur absolue d'un nombre réel x la distance entre x et 0 . On la note |x|.
Soient a et b deux nombres réels. On appelle distance entre a et b le nombre |a-b|.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Propriété

Soit x \in \R. On a |x|=\left\{\begin{array}{l}{x \quad \text { si } x \geqslant 0} \\ {-x \text { si } x\lt 0}\end{array}\right. .

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Remarque

Si a et r sont deux réels avec r > 0\:: x \in[a-r\,; a+r] \Leftrightarrow |x-a| \leqslant r.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exemples

|5|=5 et |-2|=2
x \in[-2\,; 4] \Leftrightarrow x \in[1-3\,; 1+3] \Leftrightarrow|x-1| \leqslant 3

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercices

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

14
[Représenter.]
Recopier et compléter le tableau comme dans l'exemple suivant.

Inégalité	Intervalle	Représentation graphique
2\leqslant x \leqslant 4	x\in[2\, ;4]

Inégalité	Intervalle	Représentation graphique
0\lt x \leqslant 5	x\in]0\, ;5]
	x\in]-3\, ;7[
	x\in]-\infty\, ;4]
3 \leqslant x

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

15
[Raisonner.]
Compléter avec \in ou \notin.

1. 2 ] 1\, ; 3[

2. 0 [-1\, ; 2[

3. \dfrac{1}{3} [0\, ; 3]

4. 2 ]-2\, ; 2[

5. \sqrt{2} [-3\, ; 1]

6. 0 ] 0\, ;+\infty[

7. -100 ]-\infty \, ; 1[

8. \dfrac{1}{10} [0{,}01\, ; 0{,}2[

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

16
[Calculer.]
Recopier et compléter comme dans l'exemple puis écrire sous forme mathématique en utilisant le symbole \Leftrightarrow.
Exemple :
x \in [1\, ;2] si et seulement si 3x \in [3\, ;6]
x \in [1\, ;2] \Leftrightarrow 3x \in [3\, ;6]

1. x \in [7\, ; 20 ] si et seulement si 7x \in ...

2. x \in ]-1\, ; 3 ] si et seulement si 7-x \in ...

3. x \in [-5\, ; 7 ] si et seulement si 2x+3 \in ...

4. x \in ... si et seulement si -2x \in [1\, ; +\infty [

5. x \in ... si et seulement si 3-x \in ]-\infty\, ; 6]

6. x \in ... si et seulement si 7+2x \in [-1\, ; 1]

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

17
[Représenter.]
On considère, dans le plan muni d'un repère orthonormé, l'ensemble des points \text{M}(x\, ; y) tels que :
1 \lt x \lt 4 et 5 \leqslant y \leqslant 6 .

1. Représenter graphiquement cet ensemble.
2. Reprendre la question précédente avec l'ensemble des points \text{N}(x\, ; y) tels que :
1 \leqslant 2x + 1 \leqslant 4 et 5 \lt 2 - 5y \lt 6 .

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

18
Python
[Calculer.]

On donne ci-dessous le même programme en Scratch et en Python.

Capture d'écran d'un algorithme Scratch vérifiant si une valeur x est dans l'intervalle [a, b].

def DansIntervalle(a, b, x):
	if x > a and x < b:
  	return(True)
  else:
  	return(False)

1. Que fait ce programme ?

2. Modifier ce programme pour qu'il teste si un nombre appartient à l'intervalle [a\, ; b] puis à l'intervalle ]a\, ; b] et enfin à l'intervalle [a\, ; b[ .

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

19
Python
[Calculer.]
On donne ci-dessous le même programme en Scratch et en Python.

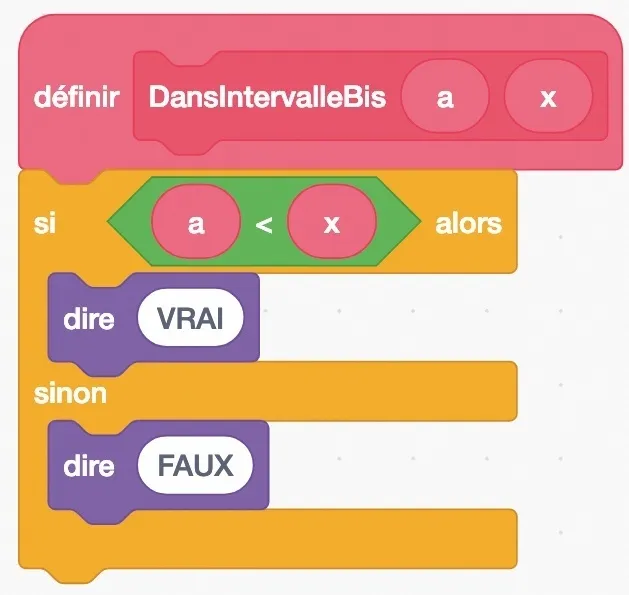
Capture d'écran d'un algorithme Scratch : test si la variable 'a' est inférieure à 'x', affichant 'VRAI' ou 'FAUX'.

def DansIntervalleBis(a, x):
	if a < x:
  	return(True)
  else:
  	return(False)

1. Que fait ce programme ?

2. Modifier ce programme pour qu'il teste si un nombre appartient à l'intervalle [a\, ; +\infty[ puis à l'intervalle ]-\infty\, ; a] et enfin à l'intervalle ]-\infty\, ; a[ .

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

20
[Représenter.]
Chaque assertion suivante est supposée vraie. Dans chaque cas, écrire, sous forme d'intervalle ou de réunion d'intervalles, le plus petit ensemble auquel appartient x .

1. x \geqslant 3 ou x \leqslant 0

2. x-6 > 0 ou 5x \leqslant 5

3. x \leqslant 2 ou -4x\leqslant -20

4. x \geqslant 3 ou 3x \geqslant 12

5. 7x-4 \geqslant 3 ou 1-x>0

6. 1-x >-3 ou 2x+1\leqslant 7

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

21
[Raisonner.]
Écrire chaque condition sous forme d'intersection et trouver l'ensemble des réels a appartenant à cette intersection.

1. a \lt 3 et a > -6

2. a \geqslant -5 et -a \geqslant -7

3. 2a+1 \lt 3 et 3a-1\geqslant 0

4. 3(2-a)\lt 3 et a-1 \geqslant 2

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Anecdote

Le symbole \infty pour représenter l'infini a été introduit par John Wallis en 1655.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

22
[Calculer.]
Parmi les nombres suivants, lesquels sont égaux à leur valeur absolue ?

1. 2

2. 3-\dfrac{8}{3}

3. 25-9 \pi

4. \dfrac{1}{2}-\dfrac{1}{3}

5. \sqrt{2}-\sqrt{5}

6. -2+9 \times(-3)

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

23
[Calculer.]
Donner la valeur absolue des nombres suivants.

1. -5

2. \dfrac{-2}{-3}

3. -\sqrt{289}

4. 3-\dfrac{2}{3} \times(6-4)

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

24
[Calculer.]
Calculer les valeurs absolues suivantes.

1. \left|10^{-7}-10^{-3}\right|

2. |17-25|

3. |1-\sqrt{2}|

4. |-3-\pi|

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

25
[Calculer.]
Dans chaque cas, donner la distance entre les deux nombres réels donnés.

1. -2 et -12

2. \dfrac{5}{3} et \dfrac{7}{6}

3. -\pi et 2\pi

4. -4 et 6

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

26
[Raisonner.]
Pour chacune des inégalités suivantes, justifier si elle est vérifiée par le nombre 2 ou non.

1. \left|x-3 \right| \leqslant 2

2. \left|x-3\right|\lt 1

3. \left|x+3 \right| \leqslant 2

4. \left|x-2 \right|\lt 1

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

27
[Calculer.]
Résoudre les équations suivantes.

1. \left|x\right|=8

2. \left|x\right|=-5

3. \left|x-1\right|=3

4. \left|2 x+1\right|=4

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

28
Vrai / Faux
[Chercher.]
Pour chaque proposition, dire si elle est vraie ou fausse en justifiant.

1. Pour tout x \in \mathbb{R}, 1+x^{2}=\left|1+x^{2}\right|.

2. Pour tout k \in \mathbb{Z}, \left|k\right|=-k.

3. Pour tout x \in \mathbb{R}, \left|(-x)^{2}\right|=-x^{2}.

4. Pour tout n \in \mathbb{N}, \left|n^{2}-n\right|=n^{2}-n.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

29
[Calculer.]
Quel est le plus grand intervalle auquel appartient x dans chacun des cas suivants ?

1. \left|x-2\right| \leqslant 3

2. x \leqslant 15

3. \left|x\right| \leqslant 1

4. 0 \leqslant x \leqslant 2

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

30
[Calculer.]
Donner un encadrement des nombres suivants à 10^-3 près.

1. \dfrac{1}{7}

2. 0{,}7586

3. \sqrt{17}

4. 2{,}356 \times 10^{-3}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

31
[Calculer.]
Donner un encadrement d'amplitude 10^-2 des nombres suivants.

1. -327{,}426

2. \dfrac{5}{8}

3. \sqrt{2}

4. 4{,}52686 \times 10^{2}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

32
[Modéliser.]
Dans la boîte de nuit le Macumba, il faut avoir strictement plus de 32 ans pour entrer. Dans la boîte de nuit la Playa, il faut avoir au plus 40 ans.

1. Dans quel intervalle d'âge doit se situer une personne qui veut pouvoir rentrer dans les deux boîtes de nuit ?

2. Dans quel ensemble doit se situer l'âge d'une personne qui veut pouvoir entrer dans l'une des deux boîtes de nuit ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

33
[Modéliser.]
L'Insee estime qu'un couple avec deux enfants appartient à la classe moyenne quand les revenus du foyer sont situés dans l'intervalle [3\, 253\, ; 5\, 609].
M. Martin gagne 2 731 € et Mme Martin gagne 2 732 €. Ils ont deux enfants qui ne rapportent aucun revenu. La famille appartient-elle à la classe moyenne ?

Page suivante

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille