1. Recopier la feuille de calcul ci-dessous.

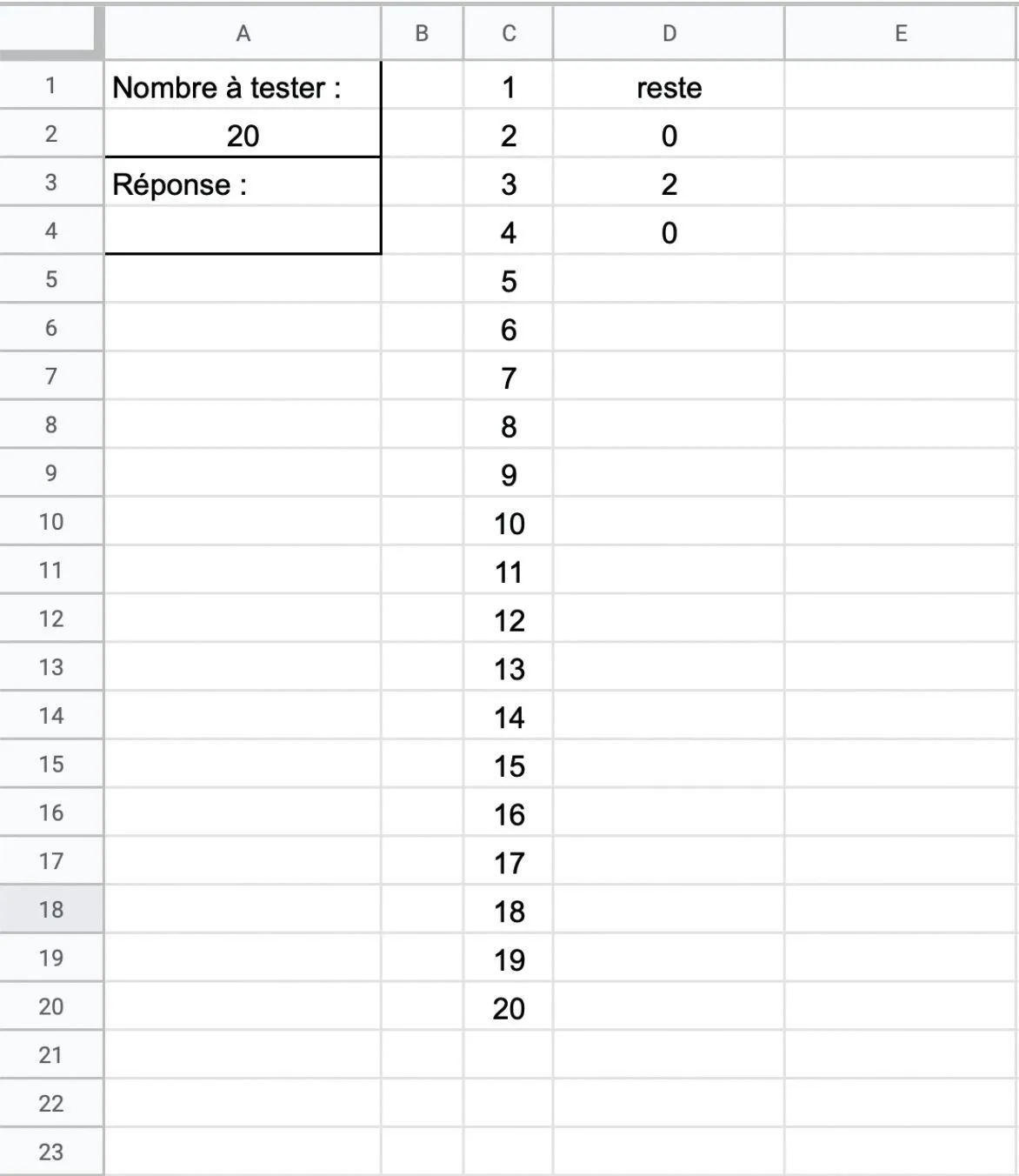
2. À l'aide de l'instruction \bf{=MOD(a\: ; b)} qui donne le reste de la division euclidienne d'un nombre entier a par un nombre entier b, écrire dans D2 une formule qui affiche le reste de la division de A2 par C2. Puis tirer cette formule vers le bas, jusqu'à la cellule D19.

3. À l'aide de la fonction \bf{= PRODUIT()} et de la fonction \bf{= SI()}, écrire une formule dans A4 qui affiche « premier » si le nombre situé en A2 est premier.

4. À l'aide de cette méthode, tester la primalité de 7 ; 29 et 91.

5. Pour n \geqslant 400 , le tableur semble ne plus pouvoir fonctionner correctement. Pour tester la primalité d'un entier inférieur à 10\,000, pourquoi est-il suffisant de tester les nombres uniquement jusqu'à 100 ? (Voir

Pour aller plus loin

ci-après.)

1. On complétera le programme ci-dessous au fur et à mesure des questions.

def Premier(nombre) :
	ntest = ...
  reponse = True
  while ... :
  	if ... :
      reponse = False
    ntest = ntest + 1
  return(...)

2. À l'aide de l'instruction \bf{a \% b} qui donne le reste de la division d'un nombre entier a par un nombre entier b , compléter le test de la ligne 5.

3. Quelle valeur doit on affecter à la variable \bf{ntest} à la ligne 2 ?

4. Compléter la ligne 4 du programme.

5. Tester la primalité de 7 ; 29 ; 91 et 529 à l'aide de cette méthode.