Vecteurs du plan

Un vecteur \overrightarrow{\text{AB}} est caractérisé par sa norme (la longueur \text{AB}), sa direction (inclinaison de la droite (\text{AB})) et son sens (de \text{A} vers \text{B}). Il définit la translation de vecteur \overrightarrow{\text{AB}} transformant \text{A} en \text{B} .

Le point \text{A} est l'origine du vecteur \overrightarrow{\text{AB}} et le point \text{B} en est l'extrémité.

On peut nommer un vecteur \overrightarrow{\text{AB}} sous la forme de vecteur \overrightarrow{u}. On note dans ce cas \overrightarrow{\text{AB}} = \overrightarrow{u} .

\overrightarrow{\text{AB}} = \overrightarrow{\text{CD}} si, et seulement si, \text{ABDC} est un parallélogramme (éventuellement aplati).

Pour tous points distincts du plan \text{A} et \text{B} : \overrightarrow{\text{AM}}=\overrightarrow{\text{MB}} si, et seulement si, \text{M} est le milieu de [\text{AB}] .

-\overrightarrow{\text{AB}}=\overrightarrow{\text{BA}}

1. On construit l'image du point \text{D} par la translation du vecteur \overrightarrow{s_{1}} , égal au vecteur \overrightarrow{s} , puis l'image du point obtenu par la translation de vecteur \overrightarrow{r_{1}} , égal au vecteur \overrightarrow{r}. On obtient ainsi le point \text{A} .

2. On construit le vecteur \overrightarrow{r^{\prime}}=\overrightarrow{r} dont l'extrémité est \text{B} . Son origine est \text{D}'.
De même on obtient \text{A}' avec le vecteur \overrightarrow{s^{\prime}}=\overrightarrow{s} d'origine \text{B}.

Pour tous points du plan \text{A} , \text{B} , \text{C} et \text{D} , on a :
1. la relation de Chasles : \overrightarrow{\text{AB}}+\overrightarrow{\text{BD}}=\overrightarrow{\text{AD}}.
2. la propriété du parallélogramme : \overrightarrow{\text{AB}}+\overrightarrow{\text{AC}}=\overrightarrow{\text{AD}} si, et seulement si, \text{ABDC} est un parallélogramme.

Relation de Chasles
La translation qui transforme \text{A} en \text{B} suivie de la translation qui transforme \text{B} en \text{D} est la translation qui transforme \text{A} en \text{D}. D'après la définition, on a bien \overrightarrow{\text{AB}}+\overrightarrow{\text{BD}}=\overrightarrow{\text{AD}}.

Propriété du parallélogramme

Si \overrightarrow{\text{AB}}+\overrightarrow{\text{AC}}=\overrightarrow{\text{AD}} alors, d'après la relation de Chasles, \overrightarrow{\text{AB}}+\overrightarrow{\text{AC}}=\overrightarrow{\text{AC}} + \overrightarrow{\text{CD}} soit encore \overrightarrow{\text{AB}} = \overrightarrow{\text{CD}}. Donc \text{ABDC} est un parallélogramme.

Réciproquement, si \text{ABDC} est un parallélogramme alors \overrightarrow{\text{AC}}=\overrightarrow{\text{BD}}. Donc \overrightarrow{\text{AB}}+\overrightarrow{\text{AC}}=\overrightarrow{\text{AB}} + \overrightarrow{\text{BD}} soit encore \overrightarrow{\text{AB}}+\overrightarrow{\text{AC}}=\overrightarrow{\text{AD}} d'après la relation de Chasles.

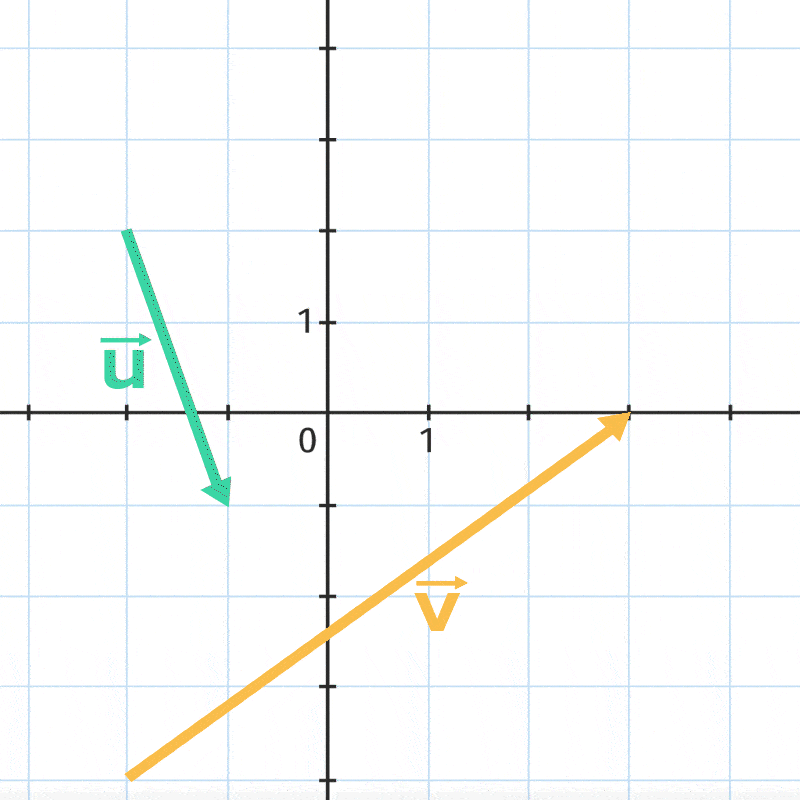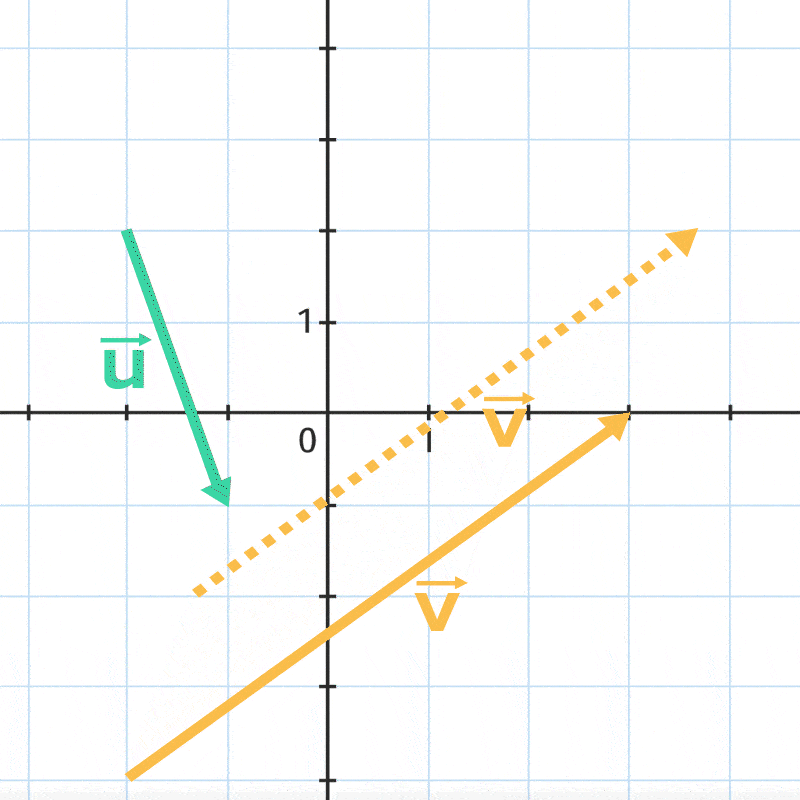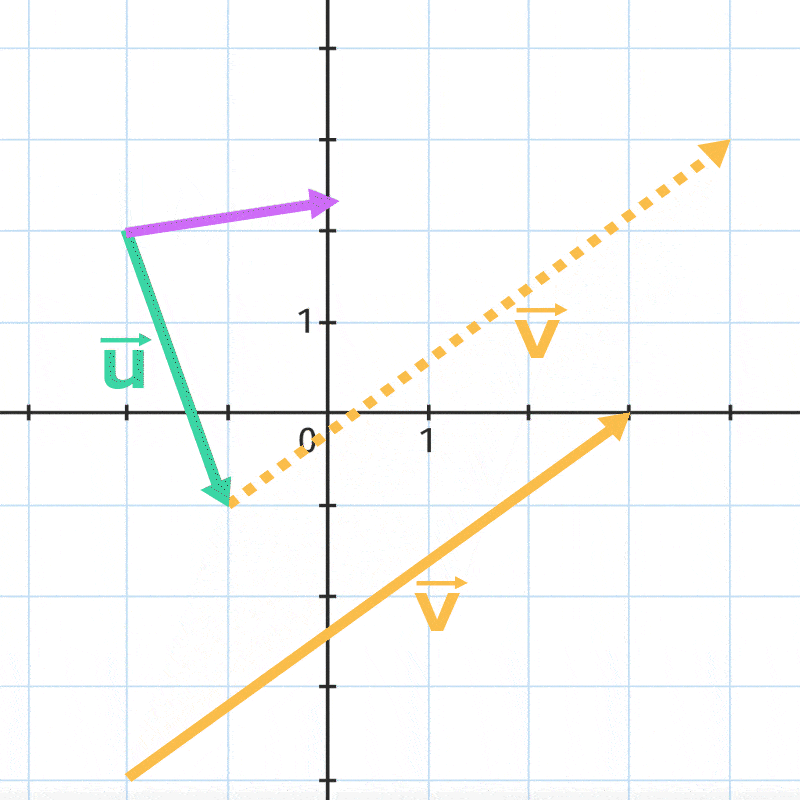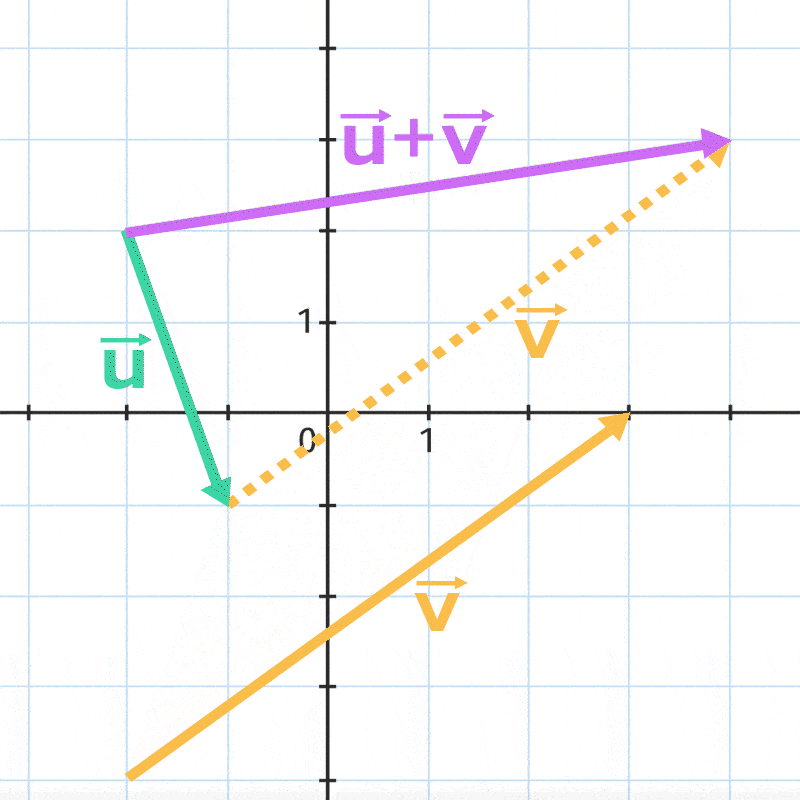
Déplacer le curseur pour tracer la somme des vecteurs \overrightarrow{u} et \overrightarrow{v}.

1. On construit le vecteur \overrightarrow{\mathrm{BB}^{\prime}} égal au vecteur \overrightarrow{\mathrm{CD}} puis, en appliquant la relation de Chasles, on obtient en vert \overrightarrow{\text{AB}^{\prime}}=\overrightarrow{\text{AB}}+\overrightarrow{\text{BB}^{\prime}} puis \overrightarrow{\mathrm{FF}^{\prime}}.

2. En appliquant la propriété du parallélogramme, on obtient en rouge \overrightarrow{\text{AA}^{\prime}}=\overrightarrow{\text{AB}}+\overrightarrow{\text{AE}} puis le vecteur \overrightarrow{c} d'origine \text{O}.