Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 6
TP / TICE 2
Somme de vecteurs
8 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Dans un repère orthonormé (\text{O} ; \text{I} , \text{J}) , on considère les points \mathrm{A}\left(x_{\mathrm{A}}\: ; y_{\mathrm{A}}\right), \mathrm{B}\left(x_{\mathrm{B}} \:; y_{\mathrm{B}}\right),
\mathrm{C}\left(x_{\mathrm{C}} \:; y_{\mathrm{C}}\right) et
\mathrm{G}\left(x_{\mathrm{G}}\: ; y_{\mathrm{G}}\right).
On s'intéresse aux conditions sur les coordonnées de \text{G} pour que \overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}=\overrightarrow{0}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Question préliminaire
Traduire l'égalité vectorielle \overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}=\overrightarrow{0} par deux égalités, l'une portant sur les abscisses des points \text{A}, \text{B}, \text{C} et \text{G} et l'autre portant sur leurs ordonnées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Observer les effets de cette égalité vectorielle en utilisant une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Python
1. a. Dans un fichier GeoGebra, placer les points
\text{A} (-2 \: ; -4), \text{B}(1 \: ; 5) et \text{C} (7 \: ; 2).
b. Créer deux curseurs x_{\text{G}} et y_{\text{G}} variant de -6 à 6.
c. Créer le point \text{G} de coordonnées (x_{\text{G}} \: ; y_{\text{G}}).
d. Construire le vecteur \overrightarrow{b} tel que \overrightarrow{b}=\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}.
b. Créer deux curseurs x_{\text{G}} et y_{\text{G}} variant de -6 à 6.
c. Créer le point \text{G} de coordonnées (x_{\text{G}} \: ; y_{\text{G}}).
d. Construire le vecteur \overrightarrow{b} tel que \overrightarrow{b}=\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}.
GeoGebra
2. En utilisant le logiciel, déterminer les valeurs des curseurs x_{\text{G}} et y_{\text{G}} pour que \overrightarrow{b} = \overrightarrow{0}.
3. En déduire les coordonnées du point \text{G} . Vérifier ce résultat avec la question préliminaire.
4. Créer le point \text{D} , milieu de [\text{AB}] et vérifier graphiquement que les points \text{D} , \text{G} et \text{C} sont alignés.
5. Afficher les longueurs \text{DG} et \text{GC} puis calculer le rapport \dfrac{\text{CG}}{\text{CD}}.
6. Reproduire la même démarche (alignement des points et rapport de longueur) en changeant les coordonnées des points \text{A} , \text{B} et \text{C} par \text{A} (-3 \: ; 1), \text{B}(6 \: ; 3) et \text{C}(6 \: ; -7).
7. Changer encore les coordonnées des points \text{A} , \text{B} et \text{C} et vérifier à chaque fois l'alignement des points \text{C} , \text{G} et \text{D} ainsi que le calcul du rapport \dfrac{\mathrm{CG}}{\mathrm{CD}}.
8. En déduire la construction du point \text{M} tel que \overrightarrow{\mathrm{MR}}+\overrightarrow{\mathrm{MS}}+\overrightarrow{\mathrm{MT}}=\overrightarrow{0} dans un triangle \text{RST} quelconque.
3. En déduire les coordonnées du point \text{G} . Vérifier ce résultat avec la question préliminaire.
4. Créer le point \text{D} , milieu de [\text{AB}] et vérifier graphiquement que les points \text{D} , \text{G} et \text{C} sont alignés.
5. Afficher les longueurs \text{DG} et \text{GC} puis calculer le rapport \dfrac{\text{CG}}{\text{CD}}.
6. Reproduire la même démarche (alignement des points et rapport de longueur) en changeant les coordonnées des points \text{A} , \text{B} et \text{C} par \text{A} (-3 \: ; 1), \text{B}(6 \: ; 3) et \text{C}(6 \: ; -7).
7. Changer encore les coordonnées des points \text{A} , \text{B} et \text{C} et vérifier à chaque fois l'alignement des points \text{C} , \text{G} et \text{D} ainsi que le calcul du rapport \dfrac{\mathrm{CG}}{\mathrm{CD}}.
8. En déduire la construction du point \text{M} tel que \overrightarrow{\mathrm{MR}}+\overrightarrow{\mathrm{MS}}+\overrightarrow{\mathrm{MT}}=\overrightarrow{0} dans un triangle \text{RST} quelconque.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
1. Dans un tableur, recopier et compléter la feuille de calcul suivante.
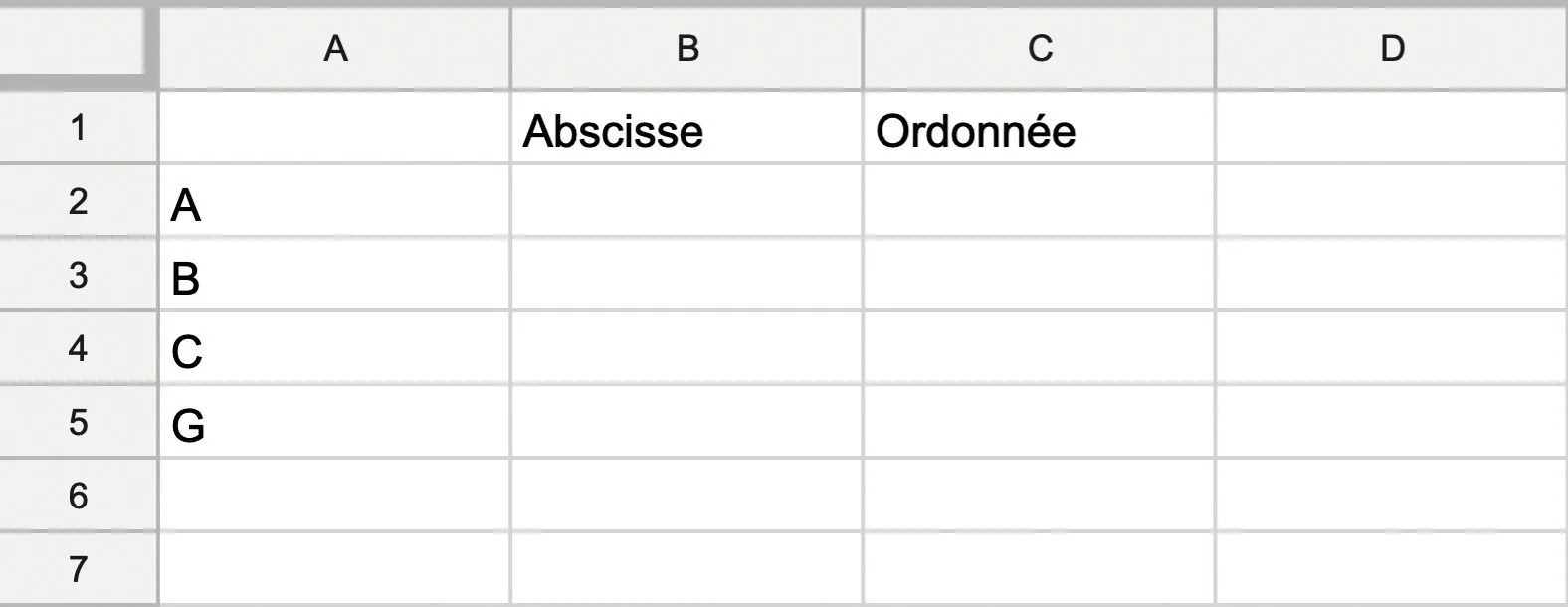
2. a. Grâce à la question préliminaire, quelles formules faut-il entrer dans les cellules B5 et C5 pour afficher les coordonnées du point \text{G} ?
b. Dans la ligne 6 du tableur, afficher l'abscisse et l'ordonnée du vecteur \overrightarrow{b}=\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}. Le résultat est-il cohérent ?
3. Soit \text{D} le milieu de [\text{AB}] . Afficher, dans la ligne 7 du tableur, les coordonnées de ce point en fonction des abscisses et des ordonnées des points \text{A} et \text{B} .
Le zoom est accessible dans la version Premium.
2. a. Grâce à la question préliminaire, quelles formules faut-il entrer dans les cellules B5 et C5 pour afficher les coordonnées du point \text{G} ?
b. Dans la ligne 6 du tableur, afficher l'abscisse et l'ordonnée du vecteur \overrightarrow{b}=\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}. Le résultat est-il cohérent ?
3. Soit \text{D} le milieu de [\text{AB}] . Afficher, dans la ligne 7 du tableur, les coordonnées de ce point en fonction des abscisses et des ordonnées des points \text{A} et \text{B} .
4. En utilisant les formules adéquates, afficher :
la valeur de la distance \text{CG}\,;
la valeur de la distance \text{GD}\,;
la valeur de la distance \text{CD}.
Que peut-on en déduire concernant les points \text{C} , \text{G} et \text{D} ?
5. Faire afficher la valeur du rapport \dfrac{\mathrm{CG}}{\mathrm{CD}}.
6. Répondre aux questions 3. et 4. en utilisant les points \text{A} , \text{B} et \text{C} définis par \text{A}(-3 \: ; 1), \text{B}(6 \: ; 3) et \text{C}(6\: ; -7).
7. Changer encore les coordonnées des points \text{A} , \text{B} et \text{C} et conjecturer la position relative des points \text{C} , \text{G} et \text{D} ainsi que la valeur du rapport \dfrac{\mathrm{CG}}{\mathrm{CD}}.
8. En déduire la construction du point \text{M} tel que \overrightarrow{\mathrm{MR}}+\overrightarrow{\mathrm{MS}}+\overrightarrow{\mathrm{MT}}=\overrightarrow{0} dans un triangle \text{RST} quelconque.
5. Faire afficher la valeur du rapport \dfrac{\mathrm{CG}}{\mathrm{CD}}.
6. Répondre aux questions 3. et 4. en utilisant les points \text{A} , \text{B} et \text{C} définis par \text{A}(-3 \: ; 1), \text{B}(6 \: ; 3) et \text{C}(6\: ; -7).
7. Changer encore les coordonnées des points \text{A} , \text{B} et \text{C} et conjecturer la position relative des points \text{C} , \text{G} et \text{D} ainsi que la valeur du rapport \dfrac{\mathrm{CG}}{\mathrm{CD}}.
8. En déduire la construction du point \text{M} tel que \overrightarrow{\mathrm{MR}}+\overrightarrow{\mathrm{MS}}+\overrightarrow{\mathrm{MT}}=\overrightarrow{0} dans un triangle \text{RST} quelconque.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah