Chapitre 12
Exercices
Travailler les automatismes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
À l'oral
Envie de réaliser ces exercices à l'oral ? Enregistrez-vous !
Enregistreur audio
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19
On considère une urne contenant cinq boules numérotées de 1 à 5. Définir deux expériences qui sont des épreuves de Bernoulli, puis deux autres qui n'en sont pas.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
On tire de manière équiprobable une carte dans un paquet de 52 cartes. On note \text{S} l'événement : « La carte est un 7. » Justifier qu'il s'agit bien d'une épreuve de Bernoulli et calculer la probabilité du succès \text{S}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
Décrire une situation concrète que l'on peut modéliser par une épreuve de Bernoulli dont le succès a pour probabilité p=0{,}13.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
Soit \text{X} la variable aléatoire qui compte le nombre de 7 obtenu en répétant dix fois l'expérience aléatoire de l'.
Quelle information manque‑t‑il à cet énoncé si on veut pouvoir conclure que \text{X} suit une loi binomiale ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
On effectue dix jets successifs d'un même dé équilibré à six faces. On nomme \text{Y} la variable aléatoire égale au plus petit résultat obtenu.
La variable \text{Y} suit�‑elle une loi binomiale ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
Soit \text{T} la variable aléatoire égale au nombre de lancers d'une pièce nécessaires pour obtenir cinq fois le côté pile.
La variable \text{T} suit‑elle une loi binomiale ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
Soit \text{Y} une variable aléatoire qui suit une loi binomiale \mathcal{B}(3~; 0{,}1). Déterminer \mathrm{E}(\mathrm{Y}), \mathrm{V}(\mathrm{Y}) et \sigma(\mathrm{Y}).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
Déterminer l'espérance de la variable \text{X} dont la distribution est représentée ci‑dessous. Justifier que \text{X} ne suit pas une loi binomiale.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Loi binomiale et calculs de probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=3 et p=0{,}95. 1. Construire l'arbre pondéré correspondant.
Cliquez pour accéder à une zone de dessin
2. En déduire \mathrm{P}(\mathrm{X}=1).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=4 et p=\frac{2}{3}.
Sans utiliser de calculatrice, calculer \mathrm{P}(\mathrm{X}=0) et \mathrm{P}(\mathrm{X}=2).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=3 et p=\frac{9}{10}. 1. Sans utiliser de calculatrice, calculer \mathrm{P}(\mathrm{X} \leqslant 1).
2. En déduire \mathrm{P}(\mathrm{X} \geqslant 2).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=4 et p=\cos \left(\frac{\pi}{4}\right).
Sans utiliser de calculatrice, calculer {\mathrm{P}(\mathrm{X}=3).}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=100 et p=0{,}15.
Calculer \mathrm{P}(\mathrm{X}=16), \mathrm{P}(\mathrm{X} \leqslant 16) et {\mathrm{P}(\mathrm{X}>16).}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=10 et p=0{,}7.
Déterminer \mathrm{P}(\mathrm{X}=6), \mathrm{P}(\mathrm{X} \leqslant 7) et {\mathrm{P}(\mathrm{X} \geqslant 5).}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=23 et p=0{,}42.
Calculer \mathrm{P}(\mathrm{X}>9), \mathrm{P}(\mathrm{X} \lt 13) et {\mathrm{P}(7 \leqslant \mathrm{X} \leqslant 10).}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34
Soit \text{X} une variable aléatoire suivant une loi binomiale de paramètres n et p=\frac{a}{100}, où a et n sont des entiers naturels.

À partir de la représentation graphique de la loi de probabilité de \text{X}, déterminer n et a.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35
On considère une variable aléatoire \text{X} qui suit la loi binomiale de paramètres n=10 et p=0{,}7.
La fonction LoiDeProbabilite ci‑dessous renvoie une liste bino telle que, pour tout entier naturel k, la valeur bino[k] est égale à \mathrm{P}(\mathrm{X}=k). La compléter.
Aide
La fonction factorial(n) permet d'obtenir n!.
from math import factorial def LoiDeProbabilite(): bino = 11*[0] for k in range(...) return bino
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36
La fonction python binomFRep ci‑dessous permet de calculer \mathrm{P}(\mathrm{X} \leqslant k) lorsque \text{X} suit une loi binomiale de paramètres n et p. La compléter.
from math import factorial def binomFRep(n, p, k): """ Si la v.a. suit une loi B(n,p), renvoie P(X <= k)""" s = 0 for i in range(...): s = s + factorial(n)/(factorial(i)*factorial(n-i))*... return s
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Espérance, variance et écart type
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=35 et p=\frac{3}{7}.
Sans utiliser de calculatrice, calculer et interpréter l'espérance de \text{X}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=75 et p=\frac{3}{5}.
Sans utiliser de calculatrice, calculer la variance et l'écart type de \text{X}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=31 et p=0{,}23.
Calculer l'espérance et la variance de \text{X}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=71 et p=\frac{7}{9}.
Calculer l'espérance et la variance de \text{X}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41
La variable aléatoire \text{X} suit une loi binomiale de paramètres n = 5 et p inconnu.
Sachant que \mathrm{E}(\mathrm{X})=3,7, déterminer p.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Introduction à l'échantillonnage
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=30 et p=0{,}23.
Déterminer le plus petit entier a tel que \mathrm{P}(\mathrm{X} \leqslant a) \geqslant 0{,}8.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=30 et p=0{,}55.
Déterminer le plus grand entier a tel que \mathrm{P}(\mathrm{X} \geqslant a) \geqslant 0{,}8.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=60 et p=0{,}45. 1. Déterminer deux entiers a et b tels que \mathrm{P}(\mathrm{X} \leqslant a) \approx 0{,}025 et \mathrm{P}(\mathrm{X} \leqslant b) \approx 0{,}975.
2. Que peut‑on alors dire de \mathrm{P}(a \leqslant \mathrm{X} \leqslant b) ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=200 et p=0{,}5. 1. Déterminer deux entiers a et b tels que \mathrm{P}(\mathrm{X} \leqslant a) \approx 0{,}05 et \mathrm{P}(\mathrm{X} \leqslant b) \approx 0{,}95.
2. Que peut‑on alors dire de \mathrm{P}(a \lt \mathrm{X} \leqslant b) ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46
Soit \text{X} une variable aléatoire qui suit la loi binomiale de paramètres n=5 et p=0{,}4. On considère la feuille de calcul suivante.

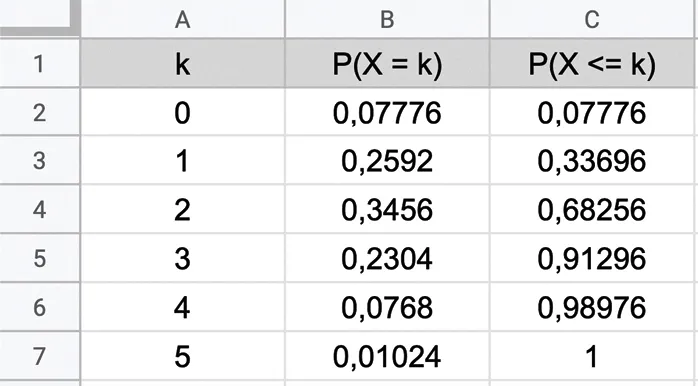


1. Quelle formule peut être entrée dans la cellule B2 puis étirée ?
2. Indiquer deux formules possibles pour obtenir le contenu de la cellule C4.
2. Indiquer deux formules possibles pour obtenir le contenu de la cellule C4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47
Déterminer le plus grand entier n tel que si \text{X} suit une loi binomiale de paramètres n et p=0{,}4, alors \mathrm{P}(\mathrm{X} \leqslant 5) \geqslant 0{,}05.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices inversés
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
Décrire une situation de la vie courante pouvant être modélisée par un schéma de Bernoulli de paramètres n=35 et p=0{,}83.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
Écrire une situation faisant intervenir la loi binomiale de paramètres n=35 et p=0{,}18.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

