Mathématiques Terminale Spécialité
Mes Pages
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 12
Entraînement 2
Loi binomiale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
Flash
Soit \text{X} une variable aléatoire suivant la loi binomiale de paramètres n=10 et p=0{,}6. Pour chacune des questions suivantes, une seule des réponses proposées est exacte. Préciser laquelle en justifiant. 1. La probabilité \mathrm{P}(\mathrm{X}=1) est égale à :
a. 10 \times 0{,}6 \times 0{,}4^{9}
b. \left(\begin{array}{c}10 \\ 1\end{array}\right) \times 0{,}6 \times 0{,}4
b. \left(\begin{array}{c}10 \\ 1\end{array}\right) \times 0{,}6 \times 0{,}4
c. 0{,}6 \times 10
d. \left(\begin{array}{c}10 \\ 1\end{array}\right)
d. \left(\begin{array}{c}10 \\ 1\end{array}\right)
2. La probabilité \mathrm{P}(\mathrm{X} \geqslant 1) est égale à :
a. \left(\begin{array}{c}10 \\ 1\end{array}\right) \times 0{,}6 \times 0{,}4^{9}
b. (1-0{,}6)^{10}
b. (1-0{,}6)^{10}
c. 1-0{,}6^{10}
d. 1-0{,}4^{10}
d. 1-0{,}4^{10}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
Flash
Soit \text{X} une variable aléatoire suivant la loi binomiale de paramètres n=25 et p=0{,}17.
En utilisant une calculatrice, donner une valeur approchée au millième des valeurs suivantes.
1. \mathrm{P}(\mathrm{X}=5)
2. \mathrm{P}(\mathrm{X} \leqslant 5)
2. \mathrm{P}(\mathrm{X} \leqslant 5)
3. \mathrm{E}(\mathrm{X})
4. \mathrm{V}(\mathrm{X})
4. \mathrm{V}(\mathrm{X})
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
Flash
Soit \text{X} une variable aléatoire suivant la loi binomiale de paramètres n=12 et p=0{,}39.
Déterminer l'entier k pour lequel la probabilité \mathrm{P}(\mathrm{X}=k) est maximale.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
Flash
Soient n un entier naturel non nul, p un réel appartenant à [0~; 1] et \text{X} une variable aléatoire suivant une loi binomiale de paramètres n et p.
Parmi les propositions suivantes, préciser, en justifiant, celles qui sont toujours vraies.
1. \mathrm{P}(\mathrm{X}=n)=\mathrm{P}(\mathrm{X} \leqslant n)
2. \mathrm{P}(\mathrm{X}=0)=\mathrm{P}(\mathrm{X} \leqslant 0)
3. À p fixé, plus n est grand, plus \mathrm{E}(\mathrm{X}) est grande.
2. \mathrm{P}(\mathrm{X}=0)=\mathrm{P}(\mathrm{X} \leqslant 0)
3. À p fixé, plus n est grand, plus \mathrm{E}(\mathrm{X}) est grande.
4. À n fixé, plus p est grand, plus \mathrm{E}(\mathrm{X}) est grande.
5. À p fixé, plus n est grand, plus \mathrm{V}(\mathrm{X}) est grande.
6. À n fixé, plus p est grand, plus \mathrm{V}(\mathrm{X}) est grande.
5. À p fixé, plus n est grand, plus \mathrm{V}(\mathrm{X}) est grande.
6. À n fixé, plus p est grand, plus \mathrm{V}(\mathrm{X}) est grande.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
[Chercher.]
Un dé à six faces non pipé est jeté sept fois de suite. La variable aléatoire \text{X} compte le nombre d'apparitions de la face 1. Quelle est la probabilité d'avoir \mathrm{X} = 7 sachant que la face 1 est apparue à chacun des six premiers jets ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
[Raisonner.]
Pour se rendre de son domicile au lycée, Kyllian doit traverser quatre passages piétons équipés d'une signalisation lumineuse. Il estime que les signalisations ne sont pas synchronisées et que la probabilité d'arriver à un passage avec un feu rouge est égale à 0{,}6. 1. En termes d'événements de probabilité, comment traduire le fait que les signalisations ne soient pas synchronisées ?
2. Aujourd'hui, à l'aller, tous les feux étaient verts. Quelle est la probabilité d'un tel événement ?
3. Lors de ce trajet, est‑il plus probable d'avoir un seul ou deux feux verts ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
[Communiquer.]
Pendant une partie de jeu de rôle, l'elfe joué par Delphine combat un troll. Deux stratégies sont possibles : une attaque normale ou une attaque spéciale. 1. Avec son attaque normale, elle doit lancer cinq dés à six faces. Pour vaincre le troll, elle doit obtenir au moins trois faces d'une valeur de 5 ou plus.
Quelle est la probabilité de le vaincre durant cette phase à l'aide d'une attaque normale ?
2. Avec une attaque spéciale, elle lance deux dés. Si elle obtient au moins un 6, l'ennemi est tué.
Quelle est la probabilité de vaincre le troll durant cette phase à l'aide d'une attaque spéciale ?
3. Quelle est l'attaque la plus efficace ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
66
[Raisonner.]
Tatiana participe à un jeu pour lequel elle doit payer 5 €. Dans un jeu de 32 cartes, elle doit tirer quatre cartes avec remise. Si elle obtient quatre as, elle gagne m €. Si elle tire un, deux ou trois as, elle gagne 10 €. Sinon, elle perd sa mise. 1. Si m=50, ce jeu est‑il équitable ? Justifier.
2. À partir de quelle valeur de m ce jeu devient‑il favorable à Tatiana ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
67
[Calculer.]
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=56 et p=0{,}13.
En détaillant la démarche, calculer les valeurs suivantes. 1. \mathrm{P}_{\mathrm{X} \leqslant 10}(\mathrm{X}=9)
2. \mathrm{P}_{\mathrm{X}>5}(\mathrm{X} \lt 15)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
68
[Calculer.]
La variable aléatoire \text{X} suit la loi binomiale de paramètres n=20 et p=0{,}65.
En utilisant éventuellement la calculatrice, calculer les valeurs suivantes.
1. \mathrm{P}(\mathrm{X}=13)
2. \mathrm{P}(\mathrm{X} \lt 15)
3. \mathrm{P}(7 \leqslant \mathrm{X} \leqslant 14)
2. \mathrm{P}(\mathrm{X} \lt 15)
3. \mathrm{P}(7 \leqslant \mathrm{X} \leqslant 14)
4. \mathrm{P}_{\mathrm{X} \lt 15}(\mathrm{X}=13)
5. \mathrm{P}_{7 \leqslant \mathrm{X} \leqslant 14}(\mathrm{X} \lt 15)
6. \mathrm{P}_{\mathrm{X} \lt 15}(7 \leqslant \mathrm{X} \leqslant 14)
5. \mathrm{P}_{7 \leqslant \mathrm{X} \leqslant 14}(\mathrm{X} \lt 15)
6. \mathrm{P}_{\mathrm{X} \lt 15}(7 \leqslant \mathrm{X} \leqslant 14)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
69
Algo
[Modéliser.]
Soit n un entier naturel non nul fixé. On lance n fois une pièce supposée équilibrée et on note, pour chaque lancer, le côté face (\text{F}) ou pile (\overline{\mathrm{F}}) obtenu. 1. Exprimer, en fonction de n, la probabilité p_n d'avoir au moins un « face » lors des n lancers.
2. Écrire un algorithme qui détermine la plus petite valeur de n telle que p_{n} \geqslant 0{,}9999.
3. Programmer cet algorithme avec Python.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
70
[Raisonner.]
On suppose que n touristes (n \geqslant 3) se retrouvent en haut de la falaise où se trouvent seulement deux chemins menant vers deux plages. Ces n touristes veulent tous se baigner et chacun d'eux choisit au hasard, de façon équiprobable et indépendamment des autres, l'une des deux directions suivantes : la plage à l'est ou la plage à l'ouest. On note \text{X} la variable aléatoire donnant le nombre de ces touristes qui choisissent la plage à l'est.
1. Déterminer la loi de probabilité suivie par \text{X}.
2. On suppose ici que les deux plages sont désertes au départ. On considère qu'un touriste est heureux s'il se retrouve seul sur une plage.
a. Peut‑il y avoir deux touristes heureux ?
b. Lorsque n=3, quelle est la probabilité d'avoir un touriste heureux ?
2. On suppose ici que les deux plages sont désertes au départ. On considère qu'un touriste est heureux s'il se retrouve seul sur une plage.
a. Peut‑il y avoir deux touristes heureux ?
b. Lorsque n=3, quelle est la probabilité d'avoir un touriste heureux ?
c. De façon générale, démontrer que la probabilité p qu'il y ait un touriste heureux parmi n touristes est p=\frac{n}{2^{n-1}}.
d. En déduire la probabilité, arrondie au centième, qu'il y ait un touriste heureux sur un groupe de dix touristes.
d. En déduire la probabilité, arrondie au centième, qu'il y ait un touriste heureux sur un groupe de dix touristes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Préciser pourquoi la variable aléatoire ne suit pas une loi binomiale en utilisant l'urne ci‑dessous.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
71
[Modéliser.]
On procède au tirage sans remise de quatre boules.
\text{X} est la variable aléatoire égale au nombre de boules rouges obtenu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
72
[Modéliser.]
On procède au tirage avec remise de quatre boules.
\text{Y} est la variable aléatoire égale au minimum des numéros obtenu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
73
[Communiquer.]
Dans chacun des cas suivants, déterminer si la variable aléatoire \text{X} suit ou non une loi binomiale en précisant les paramètres lorsque c'est le cas.
1. On lance quatre fois une pièce équilibrée.
La variable aléatoire \text{X} est égale à 1 si la même face est apparue 4 fois et à 0 sinon.
2. On lance dix fois un dé équilibré à six faces.
\text{X} est la variable aléatoire égale au plus grand résultat obtenu.
3. On lance sept fois une pièce non équilibrée telle que la probabilité d'apparition de face est le double de celle de pile. \text{X} compte le nombre d'apparitions de face.
4. On tire au hasard des cartes dans un jeu de 52 cartes.
\text{X} est la variable aléatoire donnant le nombre de cartes tirées avec remise avant d'obtenir l'as de coeur.
5. On lance un dé équilibré à six faces et on recommence tant que la face 1 n'est pas apparue.
La variable aléatoire \text{X} est égale au nombre d'apparitions de la face 4.
6. Une urne contient deux boules vertes, une boule rouge et une boule bleue. On tire avec remise quatre boules. La variable aléatoire \text{X} est égale au nombre de boules rouges obtenu.
La variable aléatoire \text{X} est égale à 1 si la même face est apparue 4 fois et à 0 sinon.
2. On lance dix fois un dé équilibré à six faces.
\text{X} est la variable aléatoire égale au plus grand résultat obtenu.
3. On lance sept fois une pièce non équilibrée telle que la probabilité d'apparition de face est le double de celle de pile. \text{X} compte le nombre d'apparitions de face.
4. On tire au hasard des cartes dans un jeu de 52 cartes.
\text{X} est la variable aléatoire donnant le nombre de cartes tirées avec remise avant d'obtenir l'as de coeur.
5. On lance un dé équilibré à six faces et on recommence tant que la face 1 n'est pas apparue.
La variable aléatoire \text{X} est égale au nombre d'apparitions de la face 4.
6. Une urne contient deux boules vertes, une boule rouge et une boule bleue. On tire avec remise quatre boules. La variable aléatoire \text{X} est égale au nombre de boules rouges obtenu.
7. Dans une urne contenant trois boules rouges et une boule noire, on prélève deux boules sans remise.
La variable aléatoire \text{X} est égale au nombre de boules rouges obtenu.
8. Dans un cinéma, lors de la projection d'un film, les personnes ayant réservé se présentent avec une probabilité égale à p=0{,}93. Il y a eu des réservations pour 100 personnes. Soit \text{X} la variable aléatoire qui donne le nombre de personnes ayant réservé qui se présentent lors de la projection.
9. On lance trois dés équilibrés à six faces. Soit \text{X} la variable aléatoire correspondant à la somme des trois faces.
10. Dans une urne contenant sept boules numérotées 0, et quatre boules numérotées 1, on prélève, avec remise, trois boules. La variable aléatoire \text{X} correspond à la somme des nombres inscrits sur les boules prélevées.
11. On prélève trois pièces, sans remise, dans un lot de 100 000 pièces contenant 1 000 pièces défectueuses.
La qualité de chaque pièce est supposée indépendante de celle des autres. La variable aléatoire \text{X} compte le nombre de pièces défectueuses obtenu.
La variable aléatoire \text{X} est égale au nombre de boules rouges obtenu.
8. Dans un cinéma, lors de la projection d'un film, les personnes ayant réservé se présentent avec une probabilité égale à p=0{,}93. Il y a eu des réservations pour 100 personnes. Soit \text{X} la variable aléatoire qui donne le nombre de personnes ayant réservé qui se présentent lors de la projection.
9. On lance trois dés équilibrés à six faces. Soit \text{X} la variable aléatoire correspondant à la somme des trois faces.
10. Dans une urne contenant sept boules numérotées 0, et quatre boules numérotées 1, on prélève, avec remise, trois boules. La variable aléatoire \text{X} correspond à la somme des nombres inscrits sur les boules prélevées.
11. On prélève trois pièces, sans remise, dans un lot de 100 000 pièces contenant 1 000 pièces défectueuses.
La qualité de chaque pièce est supposée indépendante de celle des autres. La variable aléatoire \text{X} compte le nombre de pièces défectueuses obtenu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
74
[Calculer.]
Soit \text{X} une variable aléatoire qui suit la loi binomiale de paramètres n=40 et p=0{,}31.
1. Calculer, si possible, \mathrm{P}(\mathrm{X}=11), \mathrm{P}(\mathrm{X}=13{,}5) et \mathrm{P}(\mathrm{X}=-1).
2. Calculer \mathrm{P}(\mathrm{X} \leqslant 12) et \mathrm{P}(\mathrm{X}>17).
2. Calculer \mathrm{P}(\mathrm{X} \leqslant 12) et \mathrm{P}(\mathrm{X}>17).
3. Calculer \mathrm{P}(10 \lt \mathrm{X} \leqslant 20) et \mathrm{P}(7,8 \leqslant \mathrm{X} \lt 9).
4. Calculer l'espérance, la variance et l'écart type de \text{X}.
4. Calculer l'espérance, la variance et l'écart type de \text{X}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
75
[Modéliser.]
Dans une course de 20 chevaux où tous les chevaux sont de même niveau, la probabilité qu'un parieur devine l'arrivée des quatre premiers chevaux dans l'ordre est \frac{1}{116~280}.
Pour une course, 80 000 parieurs jouent de manière indépendante et essaient de donner l'ordre d'arrivée des quatre premiers chevaux.
En utilisant une variable aléatoire suivant une loi binomiale à définir, calculer le nombre moyen, sur un très grand nombre de courses, de gagnants parmi les joueurs. On arrondira au centième.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
76
[Chercher.]
Soit \text{X} une variable aléatoire réelle qui suit une loi binomiale de paramètres n et p résumée dans le tableau ci‑dessous.
| \boldsymbol{x_i} | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| \mathbf{P}\left(\mathbf{X}=\boldsymbol{x}_{i}\right) | \frac{64}{15~625} | \frac{576}{15~625} | \frac{432}{3~125} | \frac{864}{3~125} | \frac{972}{3~125} | \frac{2~916}{15~625} | \frac{729}{15~625} |
Déterminer les valeurs des deux paramètres n et p de la loi binomiale.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
77
[Communiquer.]
Yasmine aime jouer à la roulette. Pendant une soirée, elle joue 40 fois la couleur rouge. Chaque coup, pour une mise de 1 €, elle gagne le triple de sa mise avec une probabilité égale à \frac{18}{37} et perd sa mise avec une probabilité égale à \frac{19}{37}.
Soient \text{X} et \text{G} les variables aléatoires égales respectivement au nombre de fois où Yasmine gagne et au gain algébrique (ce gain peut donc être négatif si Yasmine perd plus d'argent qu'elle n'en gagne).
Déterminer les gains maximaux, minimaux et moyens de Yasmine.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
78
[Chercher.]
Soit \text{X} une variable aléatoire.
Sachant que son espérance vaut 19{,}2 et que sa variance vaut 3{,}84, \text{X} peut‑elle suivre une loi binomiale ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
79
[Chercher.]
Soit \text{X} une variable aléatoire.
Sachant que son espérance vaut 18{,}72 et que sa variance vaut 13{,}104, \text{X} peut‑elle suivre une loi binomiale ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
80
[Calculer.]
Sven pratique le tir sportif. Il touche la cible avec une probabilité égale à \frac{3}{4}.
Pendant une séance d'entraînement, on admet que ses 60 tirs sont indépendants et réalisés dans des conditions identiques.
On note \mathrm{C} la variable aléatoire qui compte le nombre de fois où la cible est atteinte au cours de la séance. 1. Justifier que \mathrm{C} suit une loi binomiale et préciser ses paramètres.
2. Quelle est la probabilité, arrondie au millième, que Sven touche au moins 50 fois la cible pendant la séance ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
81
[Calculer.]
Dans un petit service départemental d'incendie et de secours (SDIS) du Grand Est, la variable aléatoire \text{X} donnant le nombre d'interventions quotidiennes suit la loi binomiale de paramètres n=6 et p=0{,}2. 1. Déterminer la probabilité qu'il se passe une journée sans aucune intervention.
2. Déterminer le nombre moyen d'interventions quotidiennes.
3. Sachant qu'une intervention a déjà eu lieu ce matin, quelle est la probabilité qu'il y ait au moins trois interventions aujourd'hui ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
82
Tableur
[Communiquer.]
Dominique a mis en place une feuille de calcul.
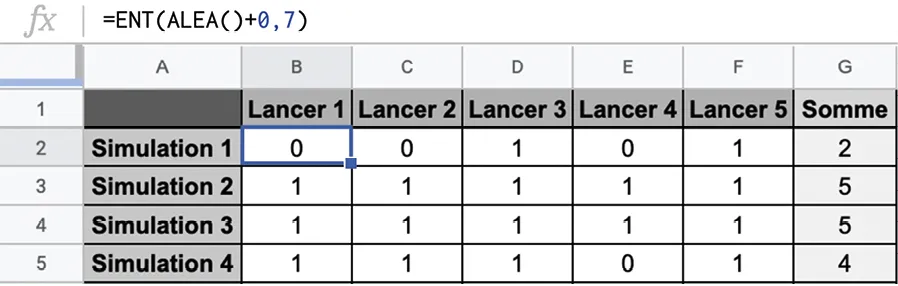
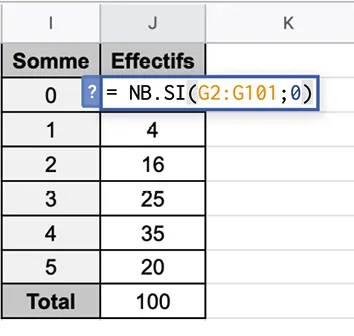
1. Expliquer ce que permettent de faire les deux formules.
2. Combien de lignes Simulation y a‑t‑il dans le document ?
2. Combien de lignes Simulation y a‑t‑il dans le document ?
3. Quel type de variable aléatoire Dominique a‑t‑il simulé ? Préciser ses paramètres.
4. Calculer la moyenne des effectifs, pondérés par les sommes. Le résultat est‑il surprenant ?
4. Calculer la moyenne des effectifs, pondérés par les sommes. Le résultat est‑il surprenant ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
83
PYTHON
[Communiquer.]
Le programme Python donné ci‑dessous simule la même expérience aléatoire que dans l'exercice précédent.
1. Expliquer ce que permettent de faire les lignes 8, 11 et 13.
2. Que renvoie ce programme ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
84
[Calculer.]
Lors de la kermesse de l'école, un jeu est organisé. Une urne contient 30 boules rouges et 10 boules noires.
Pour une mise initiale de 1 €, un joueur peut prélever au hasard et avec remise quatre boules de l'urne. Pour chaque boule noire obtenue, il gagne 1 €.
1. Quels sont les gains algébriques possibles ?
2. Quelle est la probabilité que le joueur perde 1 € ?
2. Quelle est la probabilité que le joueur perde 1 € ?
3. Quelle est la probabilité d'obtenir le gain maximal ?
4. Ce jeu est‑il équitable ? Justifier.
4. Ce jeu est‑il équitable ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
85
[Modéliser.]
Soit n un entier naturel non nul. On considère l'expérience aléatoire suivante : on lance n pièces équilibrées. Chaque pièce qui a donné pile est ensuite relancée une fois. La variable aléatoire \text{X} est égale au nombre de pile obtenu lors de la deuxième série de lancers. Déterminer la loi de probabilité suivie par \text{X}, puis son espérance et sa variance.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
86
[Calculer.]
Maxime est un cuisiner maladroit : à chaque fois qu'il fait un gâteau, il laisse tomber un œuf par terre avec une probabilité de 0{,}6. S'il laisse tomber un œuf, il devra en prendre un autre qu'il ne laissera pas tomber.
Maxime fait un gâteau par semaine et chaque gâteau nécessite un seul œuf : de combien d'œufs aura‑t‑il besoin en moyenne chaque année de 52 semaines ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
87
[Calculer.]
Un père de famille a deux filles jumelles. Chaque soir, il sort se promener avec l'une d'entre elles. Pour éviter les histoires, il choisit au hasard celle avec qui il ira se promener. Ses filles, très attachées à l'égalité, ne tolèrent chaque année (de 365 jours) que la différence de balades entre elles deux soient au maximum de six.
1. Quelle est la probabilité que, par hasard, une injustice apparaisse entre les deux sœurs ?
2. Quelle est la probabilité qu'une injustice ait lieu plus de trois fois pendant les vingt premières années de la vie des deux jumelles ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
88
Démo
[Raisonner.]
Soient n un entier naturel non nul, p un nombre réel compris entre 0 et 1 et \text{X} une variable aléatoire qui suit une loi binomiale \mathcal{B}(n~; p).
Cet exercice propose de démontrer que \mathrm{E}(\mathrm{X})=n p.
1. Démontrer que, pour tout entier k tel que 1 \leqslant k \leqslant n :
2. On rappelle que \mathrm{E}(\mathrm{X})=\mathop{\sum}\limits_{k=0}\limits^{n} k \times \mathrm{P}(\mathrm{X}=k).
Donner l'expression de \mathrm{P}(\mathrm{X}=k) lorsque 0 \leqslant k \leqslant n puis en déduire que l'espérance de \text{X} est égale à :
k\left(\begin{array}{l}n \\ k\end{array}\right)=n\left(\begin{array}{l}n-1 \\ k-1\end{array}\right).
2. On rappelle que \mathrm{E}(\mathrm{X})=\mathop{\sum}\limits_{k=0}\limits^{n} k \times \mathrm{P}(\mathrm{X}=k).
Donner l'expression de \mathrm{P}(\mathrm{X}=k) lorsque 0 \leqslant k \leqslant n puis en déduire que l'espérance de \text{X} est égale à :
\mathrm{E}(\mathrm{X})=n \mathop{\sum}\limits_{k=1}\limits^{n}\left(\begin{array}{l}n-1 \\ k-1\end{array}\right) p^{k}(1-p)^{n-k}.
Aide
k = 0 n'apparaît pas dans la somme : pourquoi ?
3. En effectuant le changement d'indice i = k - 1, montrer que \mathrm{E}(\mathrm{X})=n p \mathop{\sum}\limits_{i=0}\limits^{n-1}\left(\begin{array}{c}n-1 \\ i\end{array}\right) p^{i}(1-p)^{(n-1)-i}.
4. On admet que, pour tous réels a et b et tout n \in \mathbb{N}^{*} :
En utilisant le calcul de (p+(1-p))^{n-1}, simplifier l'écriture de \mathrm{E}(\mathrm{X}) et conclure.
4. On admet que, pour tous réels a et b et tout n \in \mathbb{N}^{*} :
(a+b)^{n}=\mathop{\sum}\limits_{i=0}\limits^{n}\left(\begin{array}{c}n \\ i\end{array}\right) a^{i} \times b^{n-i}.
En utilisant le calcul de (p+(1-p))^{n-1}, simplifier l'écriture de \mathrm{E}(\mathrm{X}) et conclure.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
