Chapitre 3
Entraînement 2
Point de vue local : nombre dérivé et tangente à la courbe
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 55
[Communiquer.]
Soit f une fonction dont on donne la représentation graphique \mathcal{C}_f ci‑dessous. On a représenté la tangente \mathrm{T}_{\mathrm{A}} à cette courbe au point \text{A} d'abscisse 2.
On admet que \mathrm{T}_{\mathrm{A}} passe par le point \mathrm{B}(0 \: ; 6).

1. Compléter la phrase suivante : « f^{\prime}(2) est le de la droite \mathrm{T}_{\mathrm{A}} ».
2. Déterminer graphiquement f^{\prime}(2).
On admet que \mathrm{T}_{\mathrm{A}} passe par le point \mathrm{B}(0 \: ; 6).

1. Compléter la phrase suivante : « f^{\prime}(2) est le
2. Déterminer graphiquement f^{\prime}(2).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 56
[Calculer.]
Soit g une fonction définie sur \R dont on donne la représentation graphique \mathcal{C}_g dans le repère ci‑dessous. On a tracé les tangentes à \mathcal{C}_g aux points d'abscisses 0, 2 et 4.

Calculer g^{\prime}(0), g^{\prime}(2) et g^{\prime}(4).

Calculer g^{\prime}(0), g^{\prime}(2) et g^{\prime}(4).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 57
[Représenter.]
Soit f la fonction définie, pour tout x strictement positif, par f(x)=\frac{1}{x}.
On note d la droite d'équation y=-4 x+4.
On admet que d est tangente à la courbe représentative de f en un point \text{A} d'abscisse a.
1. À l'aide de la calculatrice, tracer la courbe représentative de f ainsi que la droite d.
2. Déterminer, en justifiant, les coordonnées de \text{A}.
3. Déterminer sans calcul f^{\prime}(a).
On note d la droite d'équation y=-4 x+4.
On admet que d est tangente à la courbe représentative de f en un point \text{A} d'abscisse a.
1. À l'aide de la calculatrice, tracer la courbe représentative de f ainsi que la droite d.
2. Déterminer, en justifiant, les coordonnées de \text{A}.
3. Déterminer sans calcul f^{\prime}(a).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 58
[Représenter.]
Soit f une fonction dont on donne la représentation graphique \mathcal{C}_f ci‑dessous. On note \mathrm{T}_{\mathrm{A}} la tangente à cette courbe au point \text{A} d'abscisse 1.

1. Déterminer graphiquement f^{\prime}(1).
2. En déduire l'équation réduite de la tangente à la courbe représentative de f en \text{A}.

1. Déterminer graphiquement f^{\prime}(1).
2. En déduire l'équation réduite de la tangente à la courbe représentative de f en \text{A}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 59
[Représenter.]
Sur l'écran de la calculatrice, on a tracé la courbe représentative de la fonction f définie par f(x)=-x^{3}+x+2.

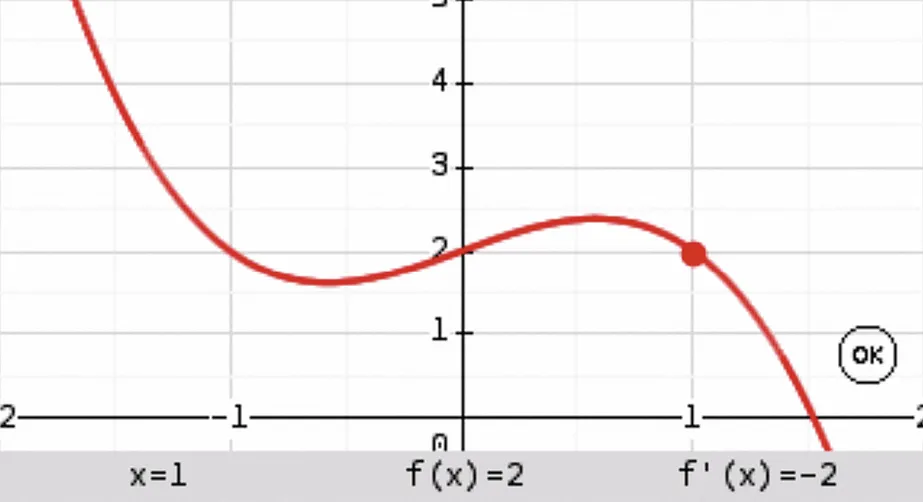
D'après les données affichées à l'écran, déterminer l'équation de la tangente à la courbe représentative de f au point d'abscisse 1.


D'après les données affichées à l'écran, déterminer l'équation de la tangente à la courbe représentative de f au point d'abscisse 1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 60
[Représenter.]
On a représenté une fonction f ainsi que la tangente \mathrm{T}_{\mathrm{A}} à sa courbe représentative au point \text{A} d'abscisse 6.

1. Par lecture graphique, déterminer f^{\prime}(6).
2. Déterminer l'équation réduite de la tangente \mathrm{T}_{\mathrm{A}}.

1. Par lecture graphique, déterminer f^{\prime}(6).
2. Déterminer l'équation réduite de la tangente \mathrm{T}_{\mathrm{A}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 61
[Raisonner.]
Soit f la fonction définie, pour tout réel x, par f(x)=x^{2}.
On se propose de déterminer f^{\prime}(3) par le calcul à l'aide des taux de variation.
1. Soit h un nombre réel.
Exprimer f(3+h) en fonction de h.
2.
On note \tau_{h}=\frac{f(3+h)-f(3)}{h} le taux de variation de f en 3. Exprimer \tau_{h} en fonction de h.
3. a. Calculer \tau_{1}, \tau_{0,1} puis \tau_{0,01}.
b. Vers quelle valeur tend \tau_{h} lorsque h se rapproche de 0 ?
4. En déduire f^{\prime}(3).
On se propose de déterminer f^{\prime}(3) par le calcul à l'aide des taux de variation.
1. Soit h un nombre réel.
Exprimer f(3+h) en fonction de h.
Aide
Pour tous réels a et b, (a+b)^{2}=a^{2}+2 a b+b^{2}.
3. a. Calculer \tau_{1}, \tau_{0,1} puis \tau_{0,01}.
b. Vers quelle valeur tend \tau_{h} lorsque h se rapproche de 0 ?
4. En déduire f^{\prime}(3).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 62
Exercice inversé
Proposer une fonction polynôme de degré 3
dont la tangente au point \mathrm{A}(1 \: ; 2) est horizontale.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 63
Exercice inversé
Proposer une fonction polynôme de degré 2 à coefficients entiers dont la tangente à la courbe représentative au point d'abscisse 1 a pour équation y=2 x-3.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

