Activité programmation

On enregistre la/les coordonnées x, ou x et y d'un point mobile à intervalles de temps connus
(\mathrm{Dt}) . \mathrm{M}_{1}\left(\begin{array}{l}{0} \\ {0}\end{array}\right) ; \mathrm{M}_{2}\left(\begin{array}{c}{1} \\ {0\text{,}125}\end{array}\right) ; \mathrm{M}_{3}\left(\begin{array}{c}{2} \\ {0\text{,}5}\end{array}\right) ; \mathrm{M}_{4}\left(\begin{array}{c}{3} \\ {1\text{,}125}\end{array}\right) ; \mathrm{M}_{5}\left(\begin{array}{l}{4} \\ {2}\end{array}\right).

\mathrm{M}_{6}\left(\begin{array}{c}{5} \\ {3\text{,}125}\end{array}\right) ; \mathrm{M}_{7}\left(\begin{array}{c}{6} \\ {4\text{,}5}\end{array}\right) ; \mathrm{M}_{8}\left(\begin{array}{c}{7} \\ {6\text{,}125}\end{array}\right) ; \mathrm{M}_{9}\left(\begin{array}{l}{8} \\ {8}\end{array}\right).

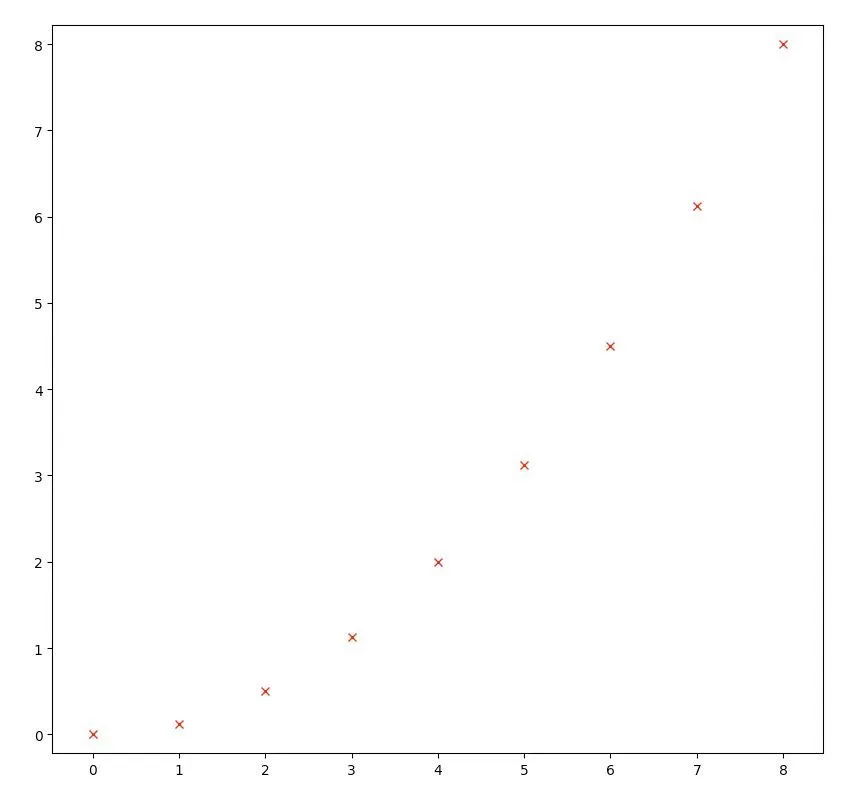
Écrire un script en langage Python permettant d'obtenir la trace de la trajectoire. On utilisera le module Python Matplotlib.

Le script doit permettre la saisie des coordonnées des points à la main et l'intervalle de temps Dt entre deux points.

Améliorations possibles

On peut ajouter la possibilité de récupérer les valeurs depuis un fichier .txt ou .csv généré par un logiciel de pointage.

• Pour que la courbe soit juste, il faut que le repère soit orthonormé. La valeur d'une graduation doit être la même en abcisse et en ordonnée.
  On utilise pour cela la commande Matplolib : plt.axis(‘equal').

Objectif de l'activité

On utilise le script précédent pour afficher la trajectoire d'un point mobile. On souhaite ensuite afficher le vecteur vitesse de ce point à une date donnée. Pour cela, il faut tracer la tangente à la courbe en ce point.

Question : rappeler la formule du vecteur vitesse au point \text{M}_{3}, approximé à la vitesse moyenne entre \text{M}_{2} et \text{M}_{4}.

Analyse du problème

Pour tracer le vecteur vitesse v_i, il faut déterminer ses coordonnées v_{x\text{i}} et v_{y\text{i}}. On les calcule à partir des coordonnées des points \text{M}_{\text{i}-1} et \mathrm{M}_{\mathrm{i}+1}.

Programmation

À partir de la fonction ci-dessous, écrire un script qui répond au cahier des charges.

def vitesse(x,y,Dt,i) :
 # x et y sont des listes contenant les coordonnées , i le numéro du point
 # dont on affiche la vitesse, Dt l'intervalle de temps entre chaque point
 # affichage du vecteur vitesse
 plt.arrow(x[i],y[i],(x[i+1]-x[i-1])/2,(y[i+1]-y[i-1])/2 , shape=‘full',lw=1,length_includes_head=True, rasterized=True, color = ‘c', head_width=.1,fc=‘c')
 # affichage de l'échelle
 plt.annotate(str(int(100/Dt)/100)+' m/s', xy=(1, 1), xytext=(max(x)-(max(x)-min(x))/5, min(y)+(max(y)-min(y))/8))
 plt.plot([max(x)-(max(x)-min(x))/5,max(x)-(max(x)-min(x))/10],[min(y)+(max(y)-min(y))/10,min(y)+(max(y)-min(y))/10],‘c')
 plt.show()