Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 1
Activités
Généralités sur les fonctions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ALe son : à consommer avec modération !
Exprimer la dépendance d'une variable par rapport à une autre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Par lecture graphique, recopier et compléter le tableau de valeurs suivant.| Distance d (en m) | 1 | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 |
| Intensité I (en dB) |
Aide
Sur quel axe doit-on lire l'intensité ? Et la distance ?
2
On donne les ordres de grandeur suivant :
- 75 dB : conversation animée ;
- 90 dB : rue à grande circulation ;
- 100 dB : seuil de danger auditif.
3
En observant le tableau de valeurs, recopier et compléter la phrase suivante : « Lorsque d double, I diminue environ de 4
Applications.
a) Préciser I pour les distances suivantes : 100 m, 25 m, 2 m et 50 cm.
b) Déterminer la distance d correspondante à 122 dB (risque desurdité) puis à 24 dB (léger fond sonore).
Aide
Utiliser le résultat de la question 3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan Une fonction a été définie ici. Quelles sont les deux variables concernées ? Quelle est celle qui dépend de l'autre ?
Bilan
Une fonction a été définie ici. Quelles sont les deux variables concernées ? Quelle est celle qui dépend de l'autre ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BLa valse des planètes
Déterminer des images et des antécédents par lecture graphique et par le calcul.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
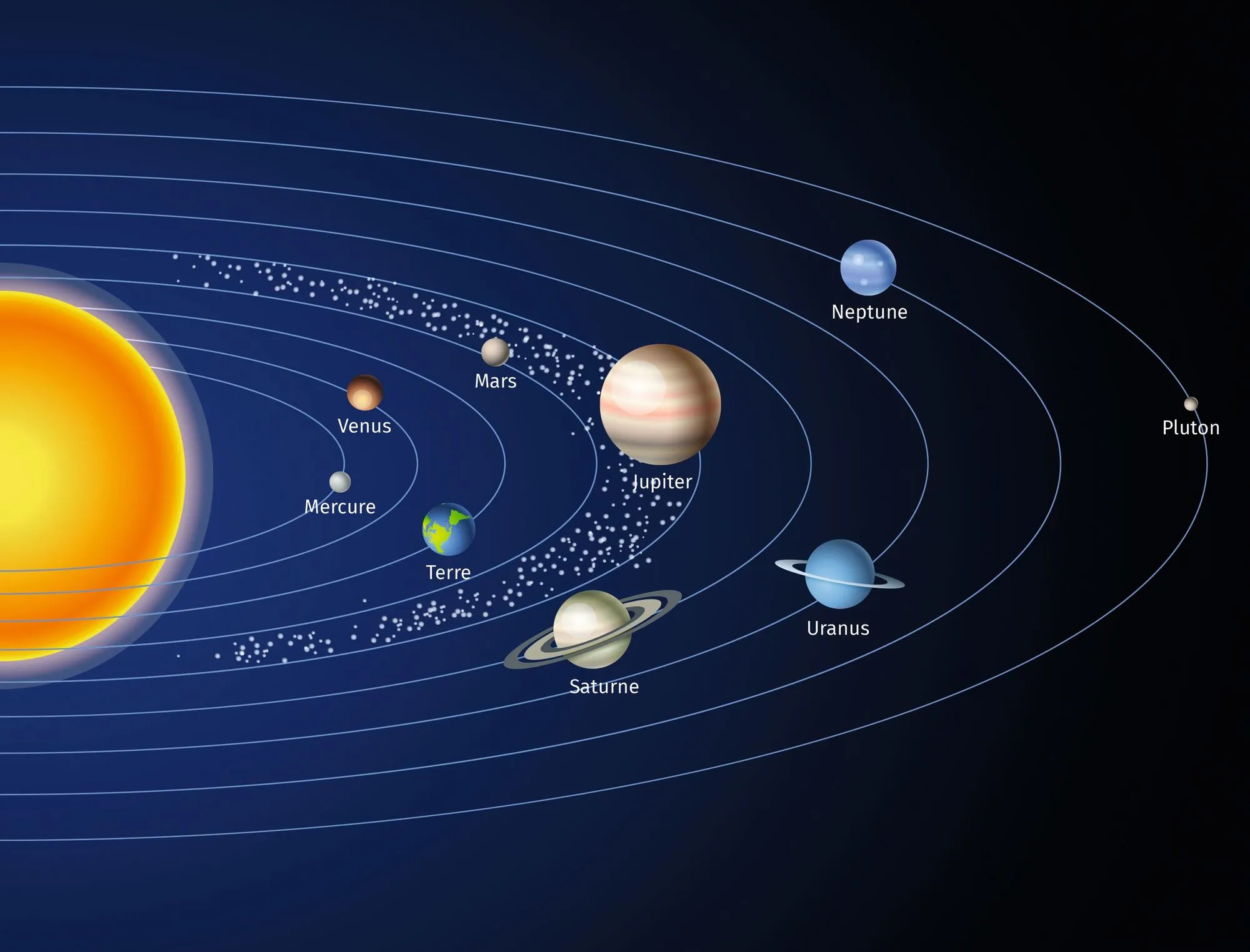
La 3e loi de Kepler indique que, pour une planète du système solaire, le carré de la période de révolution \text{P} (en seconde) est proportionnel au cube de la distance au Soleil (en mètre). Autrement dit, il existe un réel k tel que \mathrm{P}^{2}=k \times d^{3}. La constante k est exprimée en s2·m-3.
Afin de modéliser le problème, on donne :
Afin de modéliser le problème, on donne :
- la période \mathrm{P} en année terrestre ( \mathrm{P} = 1 pour la Terre) ;
- la distance d en unité astronomique (1 U.A. = distance Terre-Soleil donc d = 1 pour la Terre) ;
- la constante k égale à 1 ;
- la relation physique se ramène donc à l'égalité mathématique : \mathrm{P}^{2}=d^{3} .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
a) Calculer \mathrm{P} pour d = 1 puis d = 4.b) À l'aide la touche \sqrt[3]{ } de la calculatrice, calculer d lorsque \mathrm{P} = 8 .
c) Interpréter les résultats obtenus.
2
Recopier et compléter le tableau suivant.
| Planètes | Terre | Mars | Jupiter | Mercure | Vénus | Uranus | Neptune | Pluton | Éris |
| d (U.A.) | 1,52 | 5,2 | 0,39 | 0,72 | 19,2 | ||||
| \mathrm{P} (année) | 165 | 248 | 557 |
3
À partir de maintenant, on appelle \mathrm{P} la fonction qui, à toute distance d, fait correspondre la période
correspondante, notée \mathrm{P}(d). En utilisant le tableau précédent, donner la valeur de \mathrm{P} (1\text{,}52) et de \mathrm{P}(5\text{,}2) .
4
Pour contenir de l'eau liquide (zone d'habitabilité), on estime que l'on doit avoir 0{,}95 \leqslant d \leqslant 1{,}5 .
Calculer \mathrm{P} (0\text{,}95) et \mathrm{P} (1\text{,}5).5
a) Tracer la courbe représentative de \mathrm{P} en fonction de d pour d compris entre 0 et 6.b) Situer les différentes planètes et la zone d'habitabilité.
GeoGebra
6
Cérès est une planète naine dont la période varie entre 4 et 5 années. Préciser par lecture graphique :a) les deux planètes entre lesquelles elle se situe ;
b) les distances d minimale (périhélie) et maximale (aphélie) au Soleil.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan Quelles sont les différentes représentations de la fonction \mathrm{P} étudiées ici ? Les comparer.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CL'offre et la demande
Résoudre graphiquement des équations.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'offre et la demande sont deux notions importantes de l'économie de marché.
La demande correspond à la quantité d'un bien que les acheteurs sont prêts à acheter en fonction de différents prix.
L'offre est la quantité d'un bien que les vendeurs sont capables de vendre en fonction de différents prix.
L'offre et la demande sont donc dépendantes à la fois du prix et des quantités disponibles.
On considère un bien dont le prix p appartient à l'intervalle [60\: ; 100] et on résume les données dans le tableau de valeurs ci-dessous avec des unités fixées.
Compléter le tableau de valeurs et décrire l'offre en fonction du prix du bien. Est-ce prévisible ?
La demande correspond à la quantité d'un bien que les acheteurs sont prêts à acheter en fonction de différents prix.
L'offre est la quantité d'un bien que les vendeurs sont capables de vendre en fonction de différents prix.
L'offre et la demande sont donc dépendantes à la fois du prix et des quantités disponibles.
On considère un bien dont le prix p appartient à l'intervalle [60\: ; 100] et on résume les données dans le tableau de valeurs ci-dessous avec des unités fixées.
| Prix du bien | 10 | 30 | 50 | 80 | 100 |
| Quantité de la demande | 121 | 81 | 49 | 16 | 4 |
| Quantité de l'offre |
1
Décrire comment réagit la demande en fonction du prix du bien. Est-ce prévisible ?2
On admet que la quantité de l'offre de ce bien est définie en fonction du prix p par O(p)=\dfrac{p^{2}}{100}.Compléter le tableau de valeurs et décrire l'offre en fonction du prix du bien. Est-ce prévisible ?
3
On cherche les valeurs de p telles que O(p) = 49 . À l'aide de la calculatrice, tracer la représentation graphique de la fonction O et déterminer graphiquement une solution à cette équation. Interpréter le résultat.4
On admet que la quantité de la demande de ce bien est définie en fonction du prix p par D(p)=\dfrac{(120-p)^{2}}{100}.a) À l'aide de la calculatrice ou de GeoGebra, tracer la représentation graphique de la fonction D (en laissant apparaître celle de la fonction O).
GeoGebra
b) Déterminer le point d'intersection des représentations graphiques des fonctions O et D.
c) Quelle interprétation peut-on en faire ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan Soient f et g deux fonctions définies pour tout x \in \mathbf{D} et k un réel.
Comment résoudre graphiquement les équations f(x) = k et f(x) = g(x) ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'intensité sonore est mesurée en décibel (dB). La courbe rouge représente l'intensité sonore I lors d'un concert en fonction de la distance d des enceintes (en m), à partir d'une distance de 1 m.
Le zoom est accessible dans la version Premium.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah