Mathématiques Expertes Terminale
Mes Pages
Nombres complexes
Ch. 1
Nombres complexes, point de vue algébrique
Ch. 2
Nombres complexes, point de vue géométrique
Arithmétique
Ch. 3
Divisibilité dans Z
Ch. 4
PGCD et applications
Ch. 5
Nombres premiers
Graphes et matrices
Ch. 6
Calcul matriciel et applications aux graphes
Ch. 7
Suites et matrices
Annexes
Cahier d'algorithmique et de programmation
Chapitre 1
TP INFO 1
Suite de nombres complexes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Soient \alpha et \beta deux réels non simultanément nuls et soit q le nombre complexe q=\alpha+\mathrm{i} \beta.
On définit sur \mathbb{N} :
- une suite de nombres complexes (z_n) telle que z_0 = 1 et, pour tout entier naturel n, z_{n+1}=q z_{n} ;
- les suites de nombres réels (a_n), (b_n) et (u_n) définies, pour tout entier naturel n, par a_{n}=\operatorname{Re}\left(z_{n}\right), b_{n}=\operatorname{Im}\left(z_{n}\right) et u_{n}=\sqrt{a_{n}^{2}+b_{n}^{2}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Étudier la convergence de la suite \boldsymbol{(u_n)} pour différentes valeurs de \boldsymbol{q} à l'aide d'une des deux méthodes.
Objectif
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Question préliminaire
1. Pour cette question uniquement, on pose q=\mathrm{i}.
a. Calculer z_1, z_2, z_3 et z_4, puis en déduire les valeurs de u_0, u_1, u_2, u_3 et u_4.
b. Conjecturer, pour tout entier naturel n, une expression de u_n en fonction de n.
a. Calculer z_1, z_2, z_3 et z_4, puis en déduire les valeurs de u_0, u_1, u_2, u_3 et u_4.
b. Conjecturer, pour tout entier naturel n, une expression de u_n en fonction de n.
c. Démontrer cette conjecture et en déduire la convergence de la suite (u_n).
2. Répondre aux questions précédentes avec q=2\mathrm{i}.
Aide
On pourra démontrer que,
pour tout entier n, u_{n+1}=u_{n}.
2. Répondre aux questions précédentes avec q=2\mathrm{i}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Tableur
1. Exprimer, pour tout entier naturel n, z_{n+1} en fontion de z_n, puis a_{n+1} et b_{n+1} en fonction de a_n et de b_n.
2. À l'aide d'une feuille de calcul, on souhaite créer un tableau donnant les valeurs de a_n, b_n et u_n pour n variant de 0 à 30.
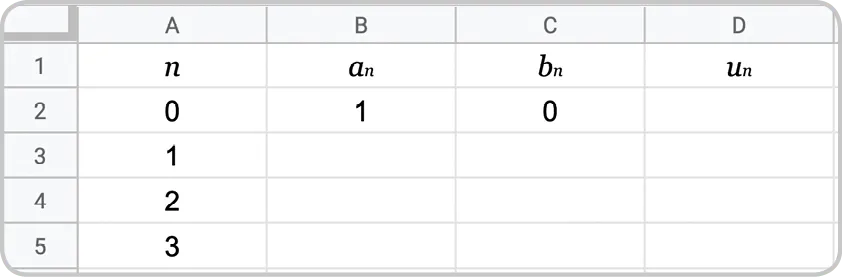
a. Quelles formules doit‑on entrer dans les cellules B3 et C3 pour obtenir les valeurs de a_n et b_n pour 1 \leqslant n \leqslant 30 par recopie vers le bas ?
2. À l'aide d'une feuille de calcul, on souhaite créer un tableau donnant les valeurs de a_n, b_n et u_n pour n variant de 0 à 30.
a. Quelles formules doit‑on entrer dans les cellules B3 et C3 pour obtenir les valeurs de a_n et b_n pour 1 \leqslant n \leqslant 30 par recopie vers le bas ?
b. Quelle formule doit‑on entrer dans la cellule D2 pour obtenir les valeurs de u_n pour 0 \leqslant n \leqslant 30 par recopie vers le bas ?
c. Quelle conjecture peut‑on faire pour la limite de la suite (u_n) ?
3. Que se passe‑t‑il lorsque q=2+2 \mathrm{i} ?
c. Quelle conjecture peut‑on faire pour la limite de la suite (u_n) ?
3. Que se passe‑t‑il lorsque q=2+2 \mathrm{i} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
1. Créer les nombres complexes \text{i} et q sur Python avec le code suivant en conjecturant le fonctionnement de la commande complex.
2. On considère la fonction z d'arguments n et q ci‑dessous. Que permet‑elle de calculer ?
3. Les commandes z.real et z.imag permettent d'obtenir respectivement les parties réelle et imaginaire du complexe z.
Écrire une fonction U prenant en argument n et q et renvoyant la valeur de u_n (penser à charger le module math pour le calcul d'une racine carrée).
4. À l'aide d'une boucle, afficher les valeurs de u_n pour l'entier n compris entre 1 et 30. Que peut‑on conjecturer à propos de la suite (u_n) ?
2. On considère la fonction z d'arguments n et q ci‑dessous. Que permet‑elle de calculer ?
3. Les commandes z.real et z.imag permettent d'obtenir respectivement les parties réelle et imaginaire du complexe z.
Écrire une fonction U prenant en argument n et q et renvoyant la valeur de u_n (penser à charger le module math pour le calcul d'une racine carrée).
4. À l'aide d'une boucle, afficher les valeurs de u_n pour l'entier n compris entre 1 et 30. Que peut‑on conjecturer à propos de la suite (u_n) ?
5. Que se passe‑t‑il lorsque q=2+2 \mathrm{i} ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
