Activités
Histoire des mathématiques
Histoire des mathématiques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AL'Algebra et il più di meno
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une équation du second degré avec Cardan
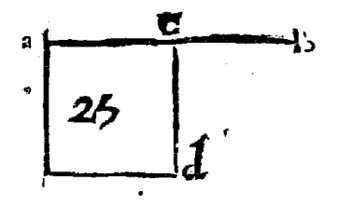
Dans son livre l'Ars Magna, Cardan s'intéresse au problème consistant à trouver deux nombres tels que leur somme soit égale à 10 et dont le produit vaut 40.


Extrait du chapitre XXXVII de l'Ars Magna de Cardan.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Montrer que le problème revient à résoudre l'équation x^{2}-10 x+40=0 et vérifier que cette équation n'a pas de solution réelle.2
Cardan utilise une méthode similaire à celle de Diophante pour la résoudre .Il explique que sa méthode donne comme solutions a=5+\sqrt{-15} et b=5-\sqrt{-15}, tout en précisant que \sqrt{-15} n'a pas de sens.
En faisant comme si \sqrt{-15} existait et vérifiait la propriété (\sqrt{x})^{2}=x valable pour tout réel positif, calculer a + b et ab. Que remarque‑t‑on ? Un nouveau nombre est né.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bombelli et les équations du troisième degré
Rafael Bombelli publie son Algebra en 1572. Pour résoudre des équations, il améliore les méthodes de Cardan‑Tartaglia‑Del Ferro, propose de nouvelles techniques, ainsi que des notations symboliques plus efficaces. De plus, il prouve que toutes les racines carrées de nombres négatifs peuvent s'écrire en fonction de \sqrt{-1} , qu'il nomme « più di meno », et que c'est un nombre comme les autres que l'on peut utiliser dans les calculs. Il donne alors les règles de signes à appliquer (en version originale ci‑contre).

Extrait de l'Algebra de Rafael Bombelli.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
À partir du texte de Bombelli, compléter le tableau ci‑dessous.
| \boldsymbol{1} | \boldsymbol{-1} | \boldsymbol{\sqrt{-1}} | \boldsymbol{-\sqrt{-1}} | |
| \boldsymbol{\sqrt{-1}} | ||||
| \boldsymbol{-\sqrt{-1}} |
Pour une équation de la forme x^{3}=p x+q, grâce à l'usage de ses notations symboliques, Bombelli montre que, lorsque \left(\frac{q}{2}\right)^{2} \geqslant\left(\frac{p}{3}\right)^{3}, une solution est égale à \sqrt[3]{\frac{q}{2}+\sqrt{\Delta}}+\sqrt[3]{\frac{q}{2}-\sqrt{\Delta}}, avec \Delta=\left(\frac{q}{2}\right)^{2}-\left(\frac{p}{3}\right)^{3}.
Remarque
- più : + (ou +1)
- meno : - (ou -1)
- uia : multiplié par
- fà : fait
- di meno : \sqrt{-1}
2
Cas de l'équation x^{3}=-6 x+20.
a) Vérifier que l'on peut appliquer la formule donnée par Bombelli.
b) Développer (1+\sqrt{3})^{3} et (1-\sqrt{3})^{3} puis, en utilisant la formule de Bombelli et le fait que \sqrt{108}=6 \sqrt{3}, déterminer une solution entière de l'équation x^{3}=-6 x+20.
3
Page 294 de son Algebra, Bombelli aborde le cas de l'équation x^{3}=15 x+4, qu'il note \mathop{\breve{1}}\limits\limits^{3}.a\mathop{\breve{15}}\limits\limits^{1}p.4.


Extrait de l'Algebra de Rafael Bombelli.
a) Expliquer pourquoi on ne peut pas appliquer la formule de Bombelli.
b) Vérifier que 4 est solution de l'équation.
c) Vérifier que les formules établies par Bombelli donneraient pour solution \sqrt[3]{2+11 \sqrt{-1}}+\sqrt[3]{2-11 \sqrt{-1}}.
d) Développer (2+\sqrt{-1})^{3} et conclure.
b) Vérifier que 4 est solution de l'équation.
c) Vérifier que les formules établies par Bombelli donneraient pour solution \sqrt[3]{2+11 \sqrt{-1}}+\sqrt[3]{2-11 \sqrt{-1}}.
d) Développer (2+\sqrt{-1})^{3} et conclure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BLa formule d'Euler
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Euler a montré que, en notation moderne, \mathrm{e}^{x}=\lim \limits_{\substack{n \rightarrow+\infty}}\left(1+\frac{x}{n}\right)^{n}.
Pour un entier naturel non nul n, il développe \left(1+\frac{x}{n}\right)^{n} et écrit :
Pour un entier naturel non nul n, il développe \left(1+\frac{x}{n}\right)^{n} et écrit :
\left(1+\frac{x}{n}\right)^{n}=1+x+\frac{n(n-1)}{2 n \times n} x^{2}+\frac{n(n-1)(n-2)}{3 n \times 2 n \times n} x^{3}+\frac{n(n-1)(n-2)(n-3)}{4 n \times 3 n \times 2 n \times n} x^{4}+\dots
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Lorsque n prend des valeurs infiniment grandes, Euler dit que 1, 2, etc. sont négligeables à côté de n.Que peut‑on alors dire des fractions \frac{n-1}{n} et \frac{(n-1)(n-2)}{2 n \times n}, lorsque n devient infiniment grand ?
2
En notant n !=n(n-1)(n-2) \times \cdots \times 2 \times 1, montrer alors que \left(1+\frac{x}{n}\right)^{n}=1+x+\frac{1}{2} x^{2}+\frac{1}{6} x^{3}+\dots+\frac{1}{j !} x^{j}+\cdots lorsque n devient infiniment grand.3
En raisonnant de façon similaire, Euler montre que \cos (x)=1-\frac{1}{2 !} x^{2}+\frac{1}{4 !} x^{4}-\frac{1}{6 !} x^{6}+\cdots et que \sin (x)=x-\frac{1}{3 !} x^{3}+\frac{1}{5 !} x^{5}-\frac{1}{7 !} x^{7}+\cdotsEn admettant que la formule \mathrm{e}^{x}=\lim \limits_{\substack{n \rightarrow+\infty}}\left(1+\frac{x}{n}\right)^{n} reste vraie lorsque x est un nombre complexe, vérifier que \cos (x)+\mathrm{i}\operatorname{sin}(x)=\mathrm{e}^{\mathrm{i} x}.




4
En prenant x = \pi, en déduire que \mathrm{e}^{\mathrm{i} \pi}+1=0.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CLes nombres complexes et la géométrie
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On munit le plan complexe d'un repère orthonormé direct (\mathrm{O}\,;\overrightarrow{u}\,,\overrightarrow{v})
Dans son programme d'Erlangen en 1872, Felix Klein caractérise les transformations du plan en utilisant les nombres complexes.
Soient \text{A} et \text{B} les points d'affixe respective a et b.
Si \text{A} est l'image de \text{B} par la rotation de centre \Omega d'affixe \omega et d'angle \theta, alors a-\omega=\mathrm{e}^{\mathrm{i} \theta}(b-\omega).
Soient \text{ABCD} un quadrilatère quelconque et \text{P}, \text{Q}, \text{R} et \text{S} les centres respectifs des carrés construits sur les côtés de \text{ABCD}, à l'extérieur de \text{ABCD}.
\text{A} est donc l'image de \text{B} par la rotation de centre \text{P} et d'angle \frac{\pi}{2}.
On appelle a, b, c, d, p, q, r et s les affixes respectives de \text{A}, \text{B}, \text{C}, \text{D}, \text{P}, \text{Q}, \text{R} et \text{S}.
Dans son programme d'Erlangen en 1872, Felix Klein caractérise les transformations du plan en utilisant les nombres complexes.
Soient \text{A} et \text{B} les points d'affixe respective a et b.
Si \text{A} est l'image de \text{B} par la rotation de centre \Omega d'affixe \omega et d'angle \theta, alors a-\omega=\mathrm{e}^{\mathrm{i} \theta}(b-\omega).
Soient \text{ABCD} un quadrilatère quelconque et \text{P}, \text{Q}, \text{R} et \text{S} les centres respectifs des carrés construits sur les côtés de \text{ABCD}, à l'extérieur de \text{ABCD}.
\text{A} est donc l'image de \text{B} par la rotation de centre \text{P} et d'angle \frac{\pi}{2}.
On appelle a, b, c, d, p, q, r et s les affixes respectives de \text{A}, \text{B}, \text{C}, \text{D}, \text{P}, \text{Q}, \text{R} et \text{S}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Montrer que p=\frac{a-\mathrm{i} b}{1-\mathrm{i}}. En procédant de même, déterminer r, s et q en fonction de a, b, c et d.2
Montrer que \frac{s-q}{r-p}=\mathrm{i}. En déduire que \mathrm{QS}=\mathrm{PR} et que (\mathrm{PS}) \perp(\mathrm{QR}).Nous venons de démontrer le théorème de Van Aubel.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

