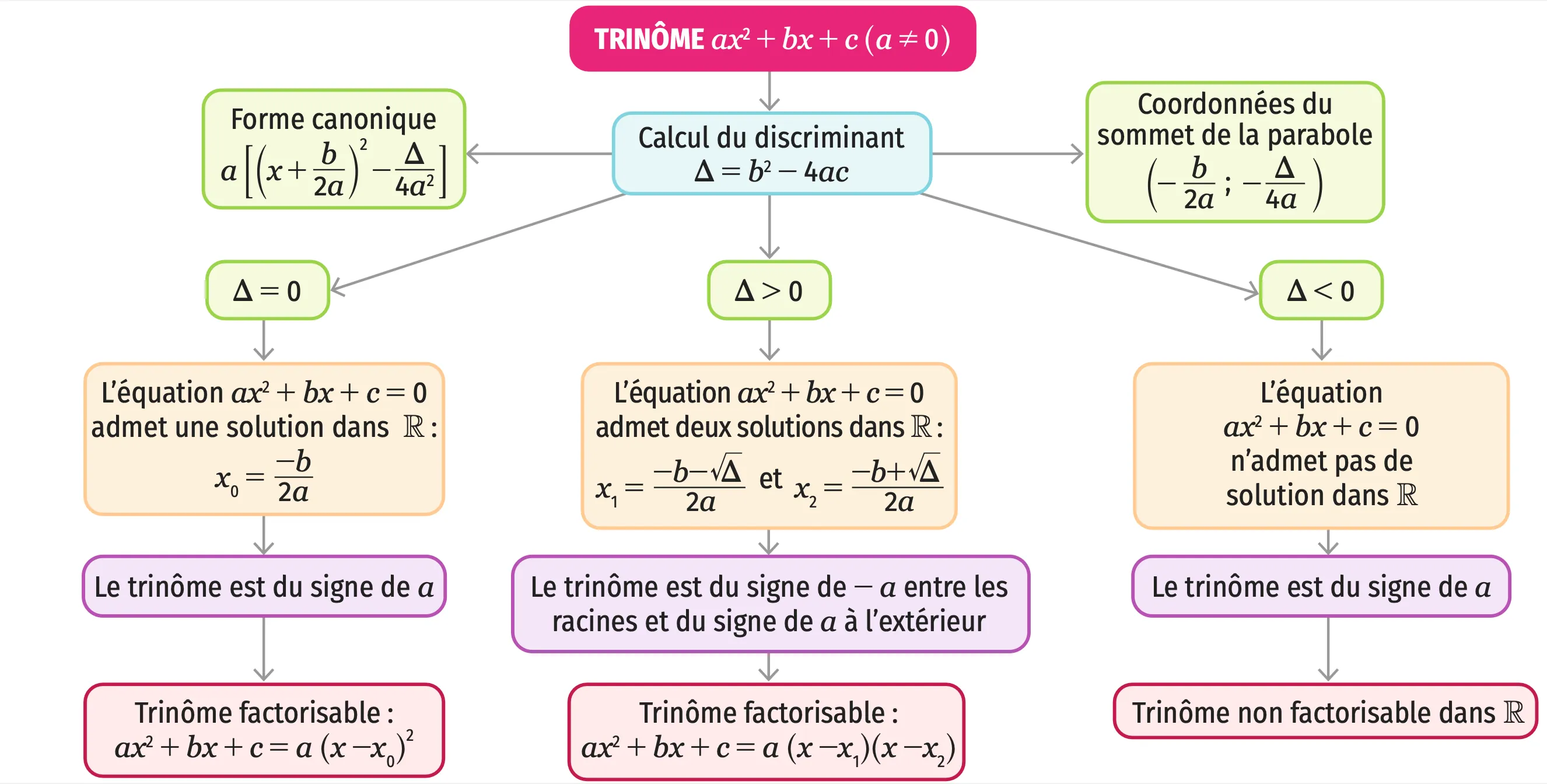
1

a, b et c sont trois réels tels que a \neq 0. a x^{2}+b x+c est un trinôme. Son discriminant est \Delta=b^{2}-4 a c.
Pour tout réel x, la forme canonique de a x^{2}+b x+c est a\left[\left(x+\dfrac{b}{2 a}\right)^{2}-\dfrac{\Delta}{4 a^{2}}\right]. Cela permet de :

✔ démontrer les autres propriétés.

2

• Si \Delta\lt0, alors l'équation a x^{2}+b x+c=0 n'a pas de solution réelle. a x^{2}+b x+c \neq 0 pour tout réel x. Il n'y a pas de factorisation possible.
• Si \Delta=0, alors l'équation a une solution réelle : x_{0}=\dfrac{-b}{2 a}. Le trinôme s'écrit \boldsymbol{a}\left(\boldsymbol{x}-\boldsymbol{x}_{\mathbf{0}}\right)^{2}.
• Si \Delta>0, l'équation a deux solutions réelles distinctes : x_{1}=\dfrac{-b-\sqrt{\Delta}}{2 a} et x_{2}=\dfrac{-b+\sqrt{\Delta}}{2 a}. Le trinôme s'écrit \boldsymbol{a}\left(\boldsymbol{x}-\boldsymbol{x}_{\mathbf{1}}\right)\left(\boldsymbol{x}-\boldsymbol{x}_{\mathbf{2}}\right).
Cela permet de :

✔ résoudre des équations polynomiales du second degré ;
✔ étudier les variations d'une fonction ou la position relative de deux courbes par exemple ;
✔ simplifier des fractions rationnelles.

3

Le trinôme a x^{2}+b x+c est du signe de a, sauf entre les racines s'il y en a. Cela permet de :

✔ donner le signe d'un trinôme ;
✔ résoudre des problèmes se ramenant à des inéquations du second degré.

4

Deux réels ont pour somme \text{S} et pour produit \text{P} si et seulement si ils sont solutions de l'équation x^{2}-\mathrm{S }x+\mathrm{P}=0. On a alors \mathrm{S}=\dfrac{\boldsymbol{-b}}{\boldsymbol{a}} et \mathrm{P} =\dfrac{\mathbf{c}}{\boldsymbol{a}}. Cela permet de :

✔ trouver la deuxième racine lorsque la première est connue (racine évidente par exemple) ;
✔ trouver deux réels dont on connaît la somme et le produit.

5

Le sommet de la parabole représentant une fonction trinôme f définie sur \R par f(x)=a x^{2}+b x+c a pour coordonnées \left(\dfrac{-b}{2 a}\text{ };\dfrac{-\Delta}{4 a}\right). Cela permet de :

✔ déterminer les coordonnées du sommet d'une parabole ;
✔ déterminer un maximum ou un minimum.