Chapitre 3
Entraînement 3
Propriétés supplémentaires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
80
[Calculer.] Pour chaque équation, déterminer une solution évidente et en déduire l'autre sans calculer le discriminant. 1. 2 x^{2}+x-3=0
2. 3 x^{2}+10 x+7=0
3. x^{2}+(\sqrt{3}-1) x-\sqrt{3}=0
4. x^{2}+4 \sqrt{5} x-25=0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
81
[Chercher.]
Trouver deux nombres dont la somme est 10 et le produit est 13.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
82
[Chercher.]
Trouver deux nombres dont la somme est 24 et le produit est 58.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
83
[Chercher.] Existe-t-il deux nombres réels dont la somme est 12 et le produit est 42 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
84
[Chercher.]
Un rectangle a pour périmètre 36 cm et pour aire 32 cm2. Déterminer les dimensions de ce rectangle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
85
[Calculer.]
Pour chacune des fonctions trinômes suivantes, calculer le discriminant ainsi que les coordonnées du sommet de sa parabole, et dresser son tableau de variations sur \R.
1. f(x)=-x^{2}+4 x-1
2. g(x)=4 x^{2}+16 x+12
Cliquez pour accéder à une zone de dessin
2. g(x)=4 x^{2}+16 x+12
Cliquez pour accéder à une zone de dessin
3. h(x)=-2 x^{2}+20 x-50
4. k(x)=10 x^{2}-30 x+\dfrac{57}{2}
Cliquez pour accéder à une zone de dessin
4. k(x)=10 x^{2}-30 x+\dfrac{57}{2}
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
86
[Chercher.]
Soit b un nombre réel et soit f la fonction trinôme définie par f(x)=-x^{2}+b x-5. On sait que f admet un extremum en 4. 1. Préciser s'il s'agit d'un minimum ou d'un maximum.
2. Déterminer la valeur de cet extremum.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
87
[Modéliser.]
Grégoire, 10 ans, veut délimiter dans son jardin un enclos rectangulaire pour son lapin nain. Son père lui donne 18 m de grillage. 1. Déterminer les dimensions de cet enclos rectangulaire qui donnent une aire maximale.
2. Quelle est alors la valeur de cette aire ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
88
[Représenter.] f et g sont deux fonctions trinômes du second degré.
L'écran de la calculatrice est abîmé et on ne peut pas lire l'expression de g(x) en fonction de x.

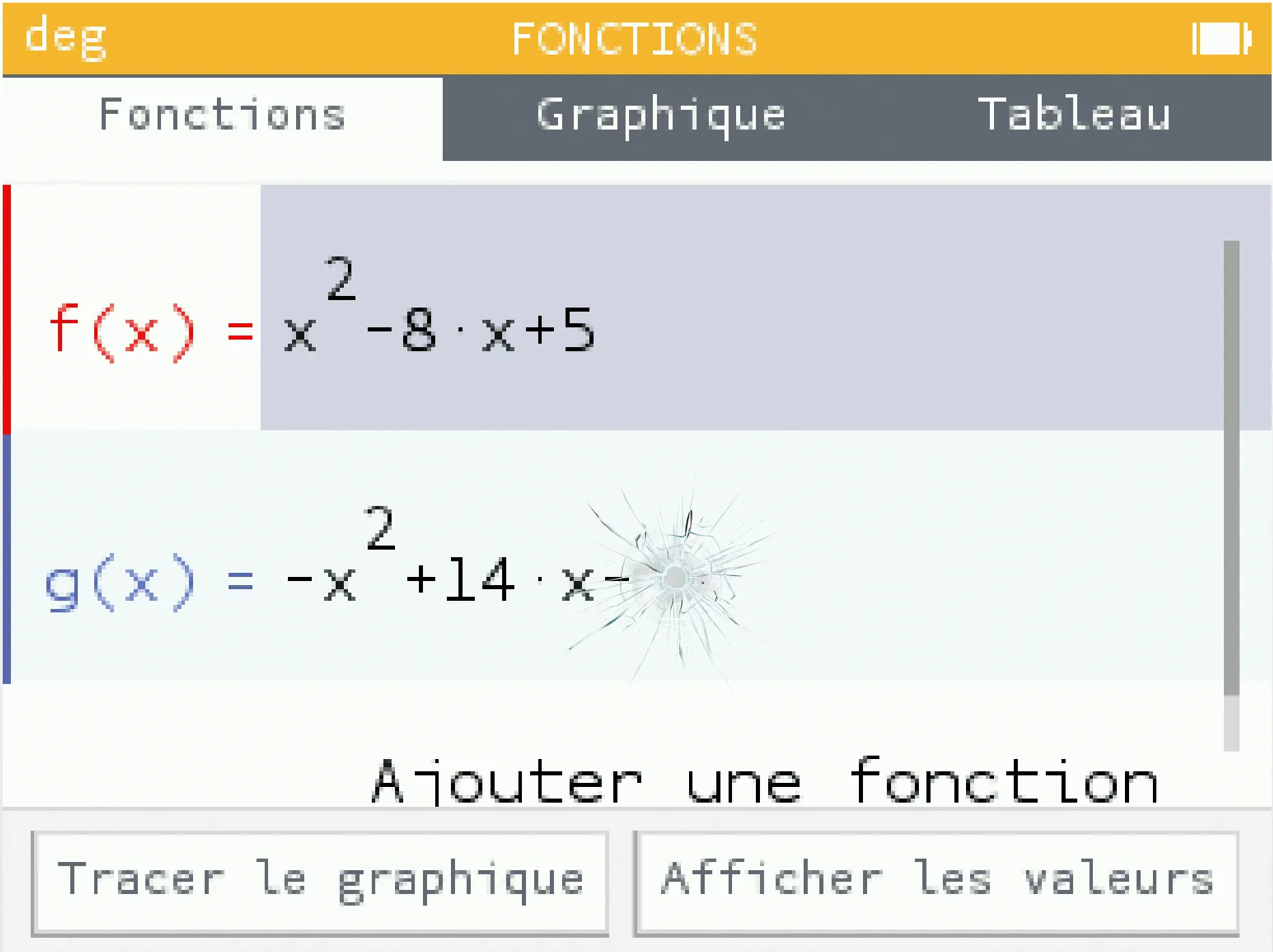

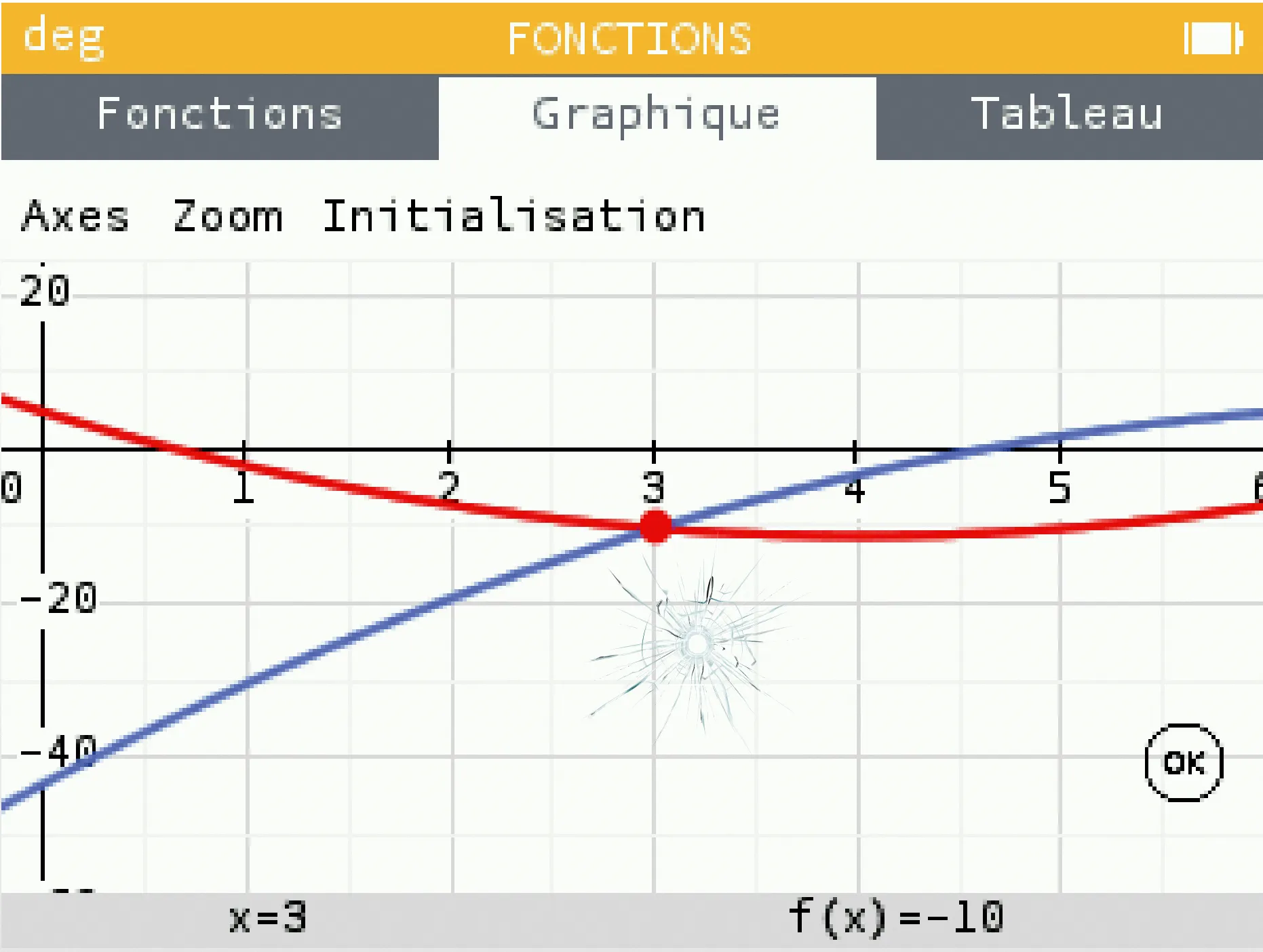
2.En déduire le coefficient manquant dans l'expression de g(x).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
89
[Chercher.]
Soit f une fonction trinôme. f admet \dfrac{-1}{2} et -3 comme racines. De plus, f admet \dfrac{-25}{8} comme extremum. Déterminer l'expression de f(x) en fonction de x.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
90
[Chercher.]
La figure ci-dessous représente le logo d'une entreprise. \text{ABCD} est un carré de côté 4 cm. \text{AFKE} et \text{KHCG} sont des carrés. Le créateur de ce logo souhaite que l'aire de la surface en bleu soit la plus petite possible.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
91
[Chercher.] Un club de vacances organise un week-end avec des activités de plein air. Le nombre maximum de participants est fixé à 60. Le prix par personne est de 50 € pour les 30 premiers. Pour tout participant supplémentaire, chaque personne bénéficie d'une remise de 1 €. Par exemple, si 35 personnes s'inscrivent à ce week-end, le prix par personne sera de 45 €. Pour quel nombre de participants, le club de vacances gagnera-t-il le plus d'argent ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
92
[Chercher.]
Le sponsor d'une célèbre équipe de football vend des maillots aux couleurs de l'équipe. Il achète ces maillots à son fournisseur au prix de 10 € l'unité. Il en vend 200 unités par jour à 50 € chacune. Au vu des bons résultats de l'équipe au cours de la saison, il souhaite augmenter le prix de ces maillots. Il réalise une étude de marché qui montre que toute augmentation de 1 € fera baisser la vente de deux maillots par jour. On admet que le nombre de maillots achetés au fournisseur est le même que le nombre de maillots vendus, quel que soit le prix.
Déterminer le nouveau prix que devra fixer le sponsor pour réaliser un bénéfice maximum.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
93
[Chercher.]
Marie-Lou et Charlotte veulent fabriquer une boîte à bijoux cylindrique pour la fête des mères. Elles disposent d'un ruban d'une longueur de 1,10 m avec lequel elles veulent entourer la boîte pour l'offrir. Elles auront besoin de 50 cm pour faire le noeud. Elles aimeraient en outre que la boîte ait la plus grande aire latérale possible pour la décorer d'un dessin.
On considère uniquement l'aire latérale \mathrm{A} du cylindre sans fond ni couvercle et, dans ce cas, \mathrm{A}=2 \pi r \times h. Déterminer le rayon et la hauteur de la boîte vérifiant ces conditions.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
94
[Chercher.]
La différence entre deux nombres est 12. Déterminer ces deux nombres sachant que la somme de leur carré est minimale.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
95
[Chercher.]
On considère la fonction trinôme du second degré f telle que :
• f(0)=3 et f(1)=-1 \: ;
• le produit de ses racines est égal à \dfrac{3}{2}. Déterminer l'expression de f(x).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
96
[Chercher.]
On considère une fonction trinôme du second degré f telle que :
• f(0)=2 et f(1)=1 \: ;
• la somme de ses racines est égale à -3 . Déterminer l'expression de f(x)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
98
[Raisonner.]
\text{ABCD} est un carré de côté 4. Soit x \in[0 \: ; 4]. \text{E} est le point de [\mathrm{AB}] tel que \mathrm{AE}=x et \text{F} est le point de [\mathrm{AD}] tel que \mathrm{DF}=x.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
97
[Raisonner.]
On donne ci-dessous les courbes représentatives de trois fonctions trinômes du second degré f en vert, g en rouge et h en bleu.

2. Déterminer, de même, les expressions de g(x) et h(x).
3. Les courbes représentatives des fonctions f, g et h ont-elles un point commun ? Si oui, déterminer ses coordonnées.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

