Nombre d'or et rectangles d'or

Le nombre d'or, noté \varphi, est un nombre étonnant qui fait parler de lui depuis l'Antiquité dans de très nombreux domaines tels que la géométrie, l'architecture, la peinture, etc. Un rectangle d'or est un rectangle dont le rapport de la longueur sur la largeur est égal au nombre d'or. Il ressemble à un rectangle tout à fait quelconque que nous pourrions tracer dans n'importe quel cours de géométrie. Si nous prenons deux livres au format poche, que nous disposons le premier à l'horizontale et le second à la verticale et que nous les alignons selon leur base, nous aurons le résultat suivant : si nous traçons la diagonale du premier livre et la prolongeons sur le deuxième, elle aboutit exactement au sommet opposé de ce dernier. Ceci est une caractéristique des rectangles d'or.
On considère deux rectangles disposés comme les deux livres de l'image. On note \text{L} la longueur des rectangles et \ell leur largeur.

GeoGebra va nous permettre de représenter les deux rectangles disposés comme les deux livres de l'image. La longueur \text{L} des rectangles est fixée à 5. On va construire une droite qui passe par la diagonale du premier rectangle comme sur l'image et on va faire varier la largeur \ell, de sorte que cette droite passe par le sommet opposé du deuxième rectangle. Le rapport \dfrac{\text{L}}{\ell}, nous donnera une valeur approchée de \varphi.

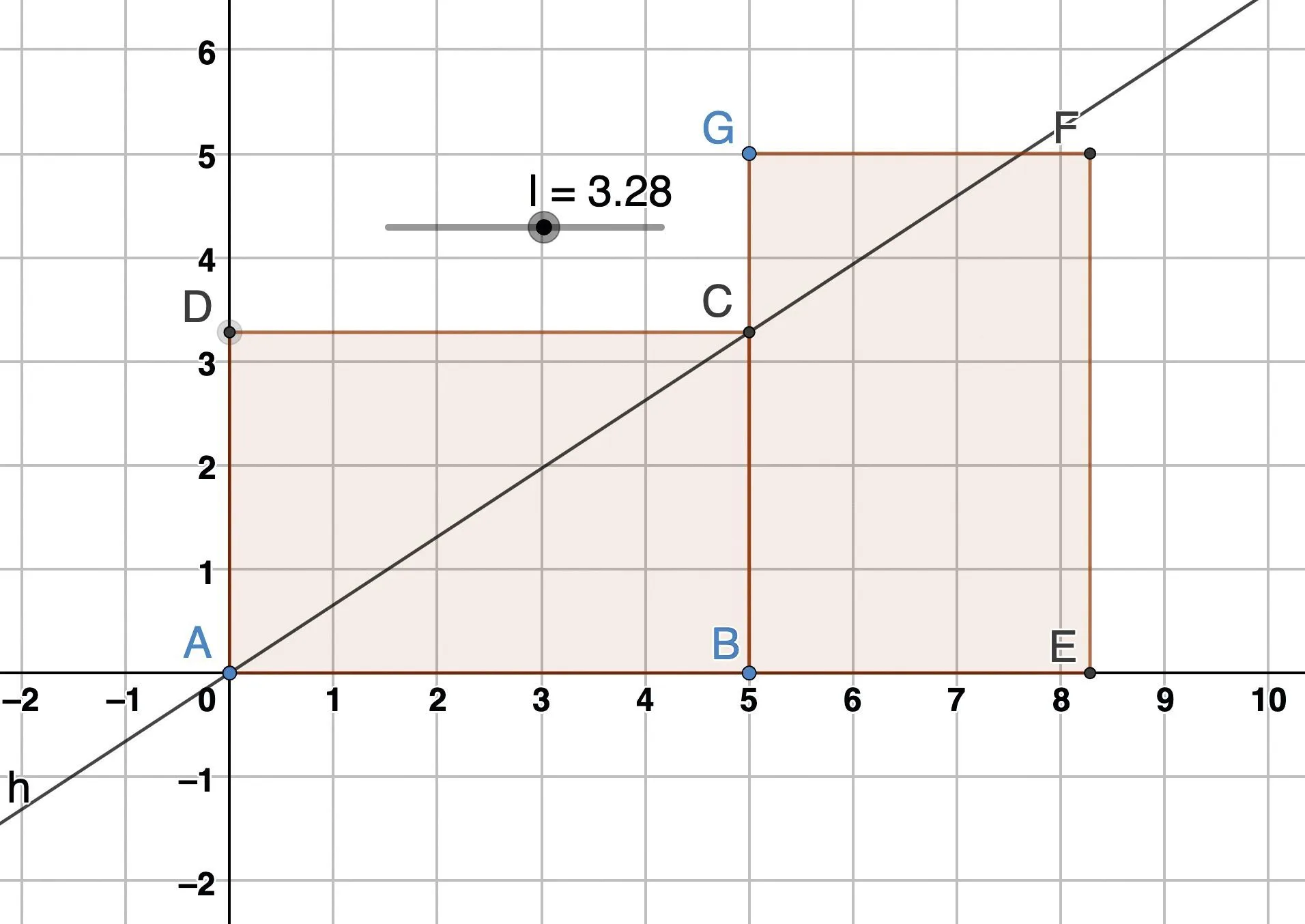1. Créer un curseur nommé \ell, variant de 1 à 5 avec une incrémentation de 0\text{,}001.
2. Créer les points \mathrm{A}(0\text{ }; 0), \mathrm{B}(5\text{ }; 0), \mathrm{C}(5\text{ }; \ell) et \mathrm{D}(0\text{ }; \ell) de sorte que \text{ABCD} forme le premier rectangle.
3. Créer les points \mathrm{E}(5+\ell\text{ }; 0), \mathrm{F}(5+\ell\text{ }; 5) et \mathrm{G}(5\text{ }; 5) pour former le deuxième rectangle \text{BEFG}.
4. Construire la droite (\text{AC}).

5. Faire varier \ell, jusqu'à ce que (\text{AC}) passe par \text{F}.
En déduire une valeur approchée de \varphi en effectuant le quotient \dfrac{\text{L}}{\ell}.

1. Déterminer en fonction de \text{L} et \ell, les coordonnées des points \text{D}, \text{E}, \text{F} et \text{G}.

2. En déduire, en fonction de \text{L} et \ell, les coordonnées des vecteurs \overrightarrow{\text{AC}} et \overrightarrow{\text{AF}}.

3. En utilisant la condition de colinéarité de deux vecteurs, montrer que les deux rectangles sont des rectangles d'or si et seulement si \text{L}^{2}-\ell \text{L}-\ell^{2}=0.

4. En fixant \mathrm{L}=2, déterminer à l'aide d'une représentation, réalisée sur la calculatrice, une valeur approchée du rapport \dfrac{\mathrm{L}}{\ell}.

5. On cherche la valeur exacte de \varphi.
a. Montrer que l'équation obtenue à la question 3. équivaut à \left(\dfrac{\text{L}}{\ell}\right)^{2}-\dfrac{\mathrm{L}}{\ell}-1=0.

b. Résoudre dans \R^+ l'équation x^{2}-x-1=0 et en déduire la valeur exacte de \varphi.