Algèbre

1. a. Calculer $u_1,u_2,u_3$ et $u_4.$ On pourra en donner une valeur approchée à 10^-2 près.

Aide

Dans cette question, il faut réaliser un calcul. La suite $\left(u_n\right)$ est définie par récurrence. Pour calculer, $u_1,$ il faut donc utiliser $u_0$ et la relation de récurrence : $u_1=\frac{u_0+2}{2u_0+1}.$
On raisonne de la même façon pour $u_2,u_3$ et $u_4.$

b. Vérifier que si $n$ est l'un des entiers $0;1;2;3$ ou $4,$ alors $u_n-1$ a le même signe que $(-1{)}^n.$
On admet que, pour tout entier naturel $n,$ $u_n-1$ a le même signe que $(-1{)}^n.$

Aide

Dans cette question, il faut réaliser une vérification.
À ne pas confondre avec une démonstration. On commence par $n=0.$ On calcule donc $u_0-1$ puis $(-1{)}^0.$
On compare les signes des deux nombres. On raisonne de la même façon pour les autres valeurs de $n$ demandées.

c. Établir que pour tout entier naturel $n,$ $u_{n+1}-1=\frac{-u_n+1}{2u_n+1}.$

Aide

Le verbe « Établir » sous-entend de réaliser une démonstration. Dans ce cas, il s'agit de démontrer une égalité : il faut donc effectuer un calcul. On utilise la relation de récurrence pour remplacer $u_{n+1}$ puis, après une réduction au même dénominateur et une simplification du membre de gauche, on doit arriver à l'expression du membre de droite.

2. a. Pour tout entier naturel $n,$ on pose $v_n=\frac{u_n-1}{u_n+1}.$ Établir que, pour tout entier naturel $n,$ $v_{n+1}=\frac{-u_n+1}{3u_n+3}.$

Aide

Une fois encore le verbe « Établir » sous-entend de réaliser une démonstration. On utilise l'expression de $v_n$ en fonction de $u_n$ pour déterminer l'expression de $v_{n+1}$ en fonction de $u_{n+1}.$ Puis, on remplace $u_{n+1}$ par sa relation de récurrence pour obtenir une expression en fonction de $u_n.$ En simplifiant, on doit retrouver l'expression du membre de droite. Il est préférable de faire séparément les calculs du numérateur et du dénominateur.

b. Démontrer que la suite $\left(v_n\right)$ est une suite géométrique de raison $\left(-\frac{1}{3}\right).$ En déduire l'expression de $v_n$ en fonction de $n.$

Aide

Il est clairement indiqué ici que l'on attend une démonstration. À ne pas confondre avec une vérification. On doit utiliser la définition du cours d'une suite géométrique : il faut trouver un réel $q$ tel que, pour tout $n\in \mathbb{N},v_{n+1}=q\times v_n.$ La deuxième partie de la question utilise également une définition du cours.

c. Démontrer que, pour tout entier naturel $n,$$u_n=\frac{1+v_n}{1-v_n},$ puis exprimer $u_n$ en fonction de $n.$

Aide

Une nouvelle démonstration par le calcul est nécessaire. Il faut utiliser l'expression de $v_n$ en fonction de $u_n$ donné au début de la question. Il faut organiser le calcul en plusieurs étapes et l'idée principale est de réussir à isoler $u_n.$ Pour cela, le terme $u_n$ ne doit apparaître qu'une seule fois. On pourra commencer par multiplier les deux membres de l'égalité par $u_n+1.$

1. Justifier que $u_1=2926.$

2. Justifier que, pour tout entier naturel $n,u_{n+1}=0\text{,}95u_n+76.$

3. À l'aide d'un tableur, on a calculé les huit premiers termes de la suite $\left(u_n\right)$. Le directeur a configuré le format des cellules pour que ne soient affichés que des nombres arrondis à l'unité.

Quelle formule peut-on entrer dans la cellule C2 afin d'obtenir, par recopie vers la droite, les termes de la suite $\left(u_n\right)?$

4. On admet que, pour tout entier naturel $n,u_n⩾1520.$ Démontrer que la suite $\left(u_n\right)$ est décroissante.

5. On désigne par $\left(v_n\right)$ la suite définie, pour tout entier naturel $n,$ par $v_n=u_n-1520.$
a. Démontrer que la suite $\left(v_n\right)$ est une suite géométrique de raison $0\text{,}95$ dont on précisera le premier terme.

b. En déduire que, pour tout entier naturel $n,$ $u_n=1480\times 0\text{,}95^n+1520.$

c. Conjecturer la valeur de $\left(u_n\right)$ lorsque $n$ devient très grand.

6. Recopier et compléter l'algorithme suivant pour déterminer l'année à partir de laquelle le nombre de cétacés présents dans la réserve marine sera inférieur à $2000.$

$\boxed{\begin{array}{l}\text{ n }\leftarrow \text{ 0 }\\ \text{ u }\leftarrow \text{ 3 000 }\\ \text{ Tant que ... }\\ \text{ n }\leftarrow \text{ ... }\\ \text{ u }\leftarrow \text{ ... }\\ \text{ Fin Tant que }\end{array}}$

7. La réserve marine fermera-t-elle un jour ? Si oui, déterminer l'année de la fermeture.

Partie A :

Pour un nombre entier naturel $n,$ on note ${\mathrm{T}}_n$ la température en degré Celsius du four au bout de $n$ heures écoulées à partir de l'instant où il a été éteint.
On a donc ${\mathrm{T}}_0=1000.$
La température ${\mathrm{T}}_n$ est calculée par l'algorithme suivant :

$\boxed{\begin{array}{l}\text{ T }\leftarrow \text{ 1 000 }\\ \text{ Pour i allant de 1 aˋ n :}\\ \text{ T }\leftarrow 0\text{,}82\times \text{T}+3\text{,}6\\ \text{ Fin Pour }\end{array}}$

1. Déterminer la température du four, arrondie à l'unité, au bout de 4 heures de refroidissement.

2. D'après l'algorithme précédent, exprimer ${\mathrm{T}}_{n+1}$ en fonction de ${\mathrm{T}}_n.$ Dans la suite, on admet que, pour tout nombre entier naturel $n,$ on a :
${\mathrm{T}}_n=980\times 0\text{,}82^n+20.$

3. À l'aide d'une

calculatrice

, déterminer au bout de combien d'heures le four peut-il être ouvert sans risque pour les céramiques.

Partie B :

Dans cette partie, on note $t$ le temps (en heure) écoulé depuis l'instant où le four a été éteint. La température du four (en degré Celsius) à l'instant $t$ est donnée par la fonction $f$ définie, pour tout nombre réel $t$ positif, par $f(t)=a{e}^{-t/5}+b,$ où $a$ et $b$ sont deux nombres réels. On admet que $f$ vérifie la relation suivante : $f^{\prime }(t)+\frac{1}{5}f(t)=4$

1. Déterminer les valeurs de $a$ et $b$ sachant qu'initialement, la température du four est de 1 000 °C, c'est-à-dire que $f(0)=1000.$

2. Pour la suite, on admet que, pour tout nombre réel positif $t,f(t)=980e^{-t/5}+20.$
a. Étudier les variations de $f$ sur $[0;+\infty [.$

b. Avec ce modèle et à l'aide d'une calculatrice, après combien de minutes le four peut-il être ouvert sans risque pour les céramiques ?

3. Dans cette question, on s'intéresse à l'abaissement de température (en degré Celsius) du four au cours d'une heure, soit entre deux instants $t$ et $(t+1).$ Cet abaissement est donné par la fonction $d$ définie, pour tout nombre réel $t$ positif, par : $d(t)=f(t)-f(t+1)$
a. Vérifier que, pour tout nombre réel $t$ positif :
$d(t)=980\left(1-e^{-1/5}\right)e^{-t/5}.$

b. À l'aide d'une calculatrice, que peut-on dire des valeurs de $d(t)$ lorsque $t$ devient de plus en plus grand.
Quelle interprétation peut-on en donner ?

Soit $u$ la suite définie par $u_0=2$ et, pour tout entier naturel $n,u_{n+1}=2u_n+2n^2-n.$
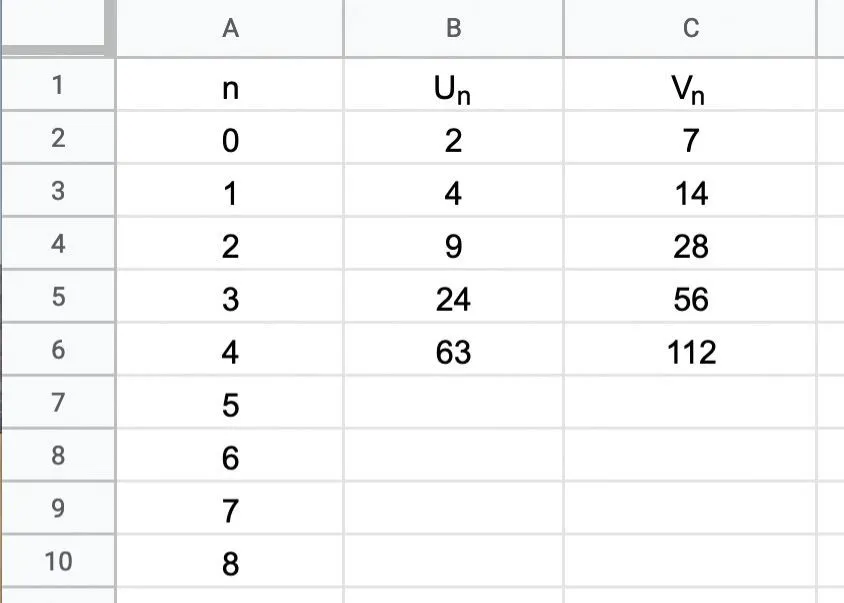
On considère également la suite $v$ définie, pour tout entier naturel $n$, par $v_n=u_n+2n^2+3n+5.$ 1. Voici, ci-dessous, un extrait de feuille de calcul. Quelles formules a-t-on écrites dans les cellules B3 et C2 et copiées vers le bas pour afficher les termes des suites $u$ et $v?$

2. À l'aide du tableur, conjecturer l'expression de $v_n$ en fonction de $n.$

GeoGebra

Accéder au module

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

3. En utilisant cette conjecture, déterminer une expression de $u_n$ en fonction de $n.$

Partie A :

On souhaite calculer les valeurs des premiers termes de la suite $\left(u_n\right)$ à l'aide d'un tableur.
On a reproduit ci-dessous une partie d'une feuille de calcul où figurent les valeurs de $u_0$ et de $u_1.$


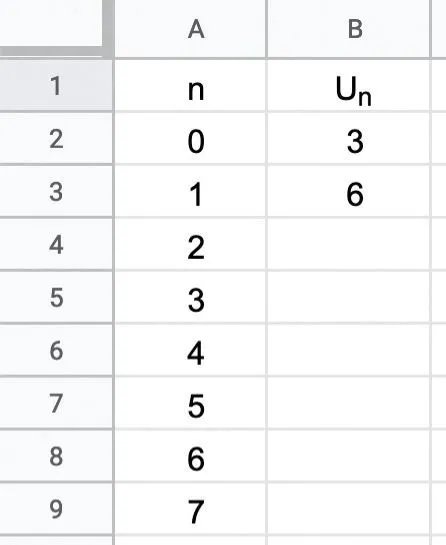
1. Donner une formule qui, saisie dans la cellule B4 puis recopiée vers le bas, permet d'obtenir des valeurs de la suite $\left(u_n\right)$ dans la colonne B.

2. Recopier et compléter le tableau ci-dessus. On donnera des valeurs approchées à 10^-3 près de $u_n$ pour $n$ allant de 2 à 5.


3. Que peut-on conjecturer à propos de la limite de la suite $\left(u_n\right)?$

Partie B : Étude de la suite
On considère les suites $\left(v_n\right)$ et $\left(w_n\right)$ définies pour tout entier naturel $n$ par : $v_n=u_{n+1}-\frac{1}{4}{u}_n$ et $w_n=u_n-7.$

1. a. Démontrer que $\left(v_n\right)$ est une suite constante.

b. En déduire que, pour tout entier naturel $n,$ $u_{n+1}=\frac{1}{4}{u}_n+\frac{21}{4}.$

2. a. Démontrer que $\left(w_n\right)$ est une suite géométrique dont on précisera le premier terme et la raison.

b. En déduire que, pour tout entier naturel $n,$ $u_n=7-{\left(\frac{1}{4}\right)}^{n-1}.$

c. Quel lien peut-on faire avec la question 3. de la partie A ?

1. a. Complétez l'arbre de probabilité relatif aux trois premières semaines ci-dessous (vous pouvez utiliser l'outil de dessin en mode zoom).

b. Démontrer que $\text{P}\left(A_3\right)=0,85.$

c. Sachant que le client achète un melon au cours de la semaine 3, quelle est la probabilité qu'il en ait acheté un au cours de la semaine 2 ? Arrondir au centième.

Dans la suite, on pose pour tout entier $n⩾1:$ $p_n=\mathrm{P}\left({\mathrm{A}}_n\right).$ On a ainsi $p_1=1$

2. Démontrer que, pour tout entier $n⩾1:$ $p_{n+1}=0\text{,}5p_n+0\text{,}4.$

3. a. On admet que, pour tout entier $n⩾1,p_n>0\text{,}8.$
Démontrer que la suite $\left(p_n\right)$ est décroissante.

b. À l'aide de la

calculatrice

, conjecturer la limite de la suite $\left(p_n\right)$.

4. On pose, pour tout entier $n⩾1:v_n=p_n-0\text{,}8.$
a. Démontrer que $\left(v_n\right)$ est une suite géométrique dont on donnera le premier terme $v_1$ et la raison.

b. Exprimer $v_n$ en fonction de $n.$

c. En déduire que, pour tout entier $n⩾1:$ $p_n=0\text{,}8+0\text{,}2\times 0\text{,}{5}^{n-1}.$

d. À l'aide de la

calculatrice

, conjecturer le comportement de $\left(p_n\right)$ lorsque $n$ devient très grand.
Interpréter le résultat.

On considère la suite $\left(u_n\right)$ définie par $u_0=1$ et pour tout $n\in \mathbb{N},u_{n+1}=\frac{1}{3}{u}_n+n-2.$ 1. Calculer $u_1,u_2$ et $u_3.$

2. À l'aide de la calculatrice, conjecturer la limite de la suite $\left(u_n\right)$ lorsque $n$ devient très grand.

3. On définit la suite $\left(v_n\right)$ par : pour tout $n\in \mathbb{N},$
$v_n=-2u_n+3n-\frac{21}{2}.$
a. Démontrer que la suite $\left(v_n\right)$ est une suite géométrique dont on donnera la raison et le premier terme.

b. En déduire que, pour tout $n\in \mathbb{N},$ $u_n=\frac{25}{4}{\left(\frac{1}{3}\right)}^n+\frac{3}{2}n-\frac{21}{4}.$

c. Soit ${\text{S}}_n$ la somme définie pour tout entier naturel $n$ par : ${\mathrm{S}}_n=\sum _{k=0}^n{u}_k=u_0+u_1+\dots +u_n.$
Déterminer l'expression de ${\text{S}}_n$ en fonction de $n.$

1. Démontrer que $f$ est croissante sur l'intervalle $[0;+\infty [.$

2. Résoudre l'équation $f(x)=x$ sur l'intervalle $[0;+\infty [.$
On note $\alpha$ la solution.
On donnera la valeur exacte de $\alpha$ puis une valeur approchée à $10^{-2}$ près.

3. On considère la suite $\left(u_n\right)$ définie par $u_0=1$ et, pour tout entier naturel $n,$ $u_{n+1}=f\left(u_n\right).$
a. Tracer, dans un repère orthonormé d'unité 2 cm, la courbe $\mathcal{C}$ représentative de $f$ ainsi que la droite $\mathcal{D}$ d'équation $y=x.$

b. En utilisant la courbe $\mathcal{C}$ et la droite $\mathcal{D},$ placer les points ${\mathrm{M}}_0,{\mathrm{M}}_1$ et ${\mathrm{M}}_2$ d'ordonnée nulle et d'abscisses respectives $u_0,u_1$ et $u_2.$
Quelles conjectures peut-on faire sur le sens de variation et la limite de la suite $\left(u_n\right)?$

4. Pour tout entier naturel $n,$ on définit la suite $\left({\mathrm{S}}_n\right)$ par ${\mathrm{S}}_n=\sum _{k=0}^n{u}_k=u_0+u_1+\dots +u_n.$
a. Calculer ${\mathrm{S}}_0,{\mathrm{S}}_1$ et ${\mathrm{S}}_1.$ Donnerune valeur approchée des résultats à $10^{-2}$ près.

b. Compléter l'algorithme ci-dessous pour qu'il calcule la somme ${\mathrm{S}}_n$ pour une valeur de $n$ donnée.

$\boxed{\begin{array}{l}\text{ u }\leftarrow \text{ 1 }\\ \text{ s }\leftarrow \text{ u }\\ \text{ i }\leftarrow \text{ 0 }\\ \text{ Tant que ... }\\ \text{ i }\leftarrow \text{ i+1 }\\ \text{ u }\leftarrow \text{ ... }\\ \text{ s }\leftarrow \text{ ... }\\ \text{ Fin Tant que}\end{array}}$

Partie A :

1. On souhaite écrire un algorithme calculant, pour un entier naturel $n$ donné, tous les termes de la suite, du rang $0$ au rang $n.$ Parmi les deux algorithmes suivants, un seul convient.
Préciser lequel en justifiant la réponse.

$\boxed{\begin{array}{l}\text{ Algorithme 1 }\\ \\ \text{ v }\leftarrow \text{ 1 }\\ \text{ Pour i variant de 1 aˋ n }:\\ \text{v}\leftarrow \frac{9}{6-\text{v}}\\ \text{Fin Pour}\end{array}}$ $\boxed{\begin{array}{l}\text{ Algorithme 2 }\\ \\ \text{ Pour i variant de 1 aˋ n }:\\ \text{ v }\leftarrow \text{ 1 }\\ \text{ v }\leftarrow \frac{9}{6-\text{v}}\\ \text{Fin Pour}\end{array}}$

2. Pour $n=10$ on obtient les valeurs suivantes :

1

1,8

2,143

2,333

2,455

2,538

2,6

2,647

2,684

2,714

Pour $n=100,$ les derniers termes calculés sont :

2,967

2,968

2,968

2,969

2,969

2,969

2,970

2,970

2,970

2,970

Quelles conjectures peut-on émettre concernant la suite $\left(v_n\right)?$

3. On admet que, pour tout entier naturel $n,0<v_n<3.$
Démontrer que, pour tout entier naturel $n,$ $v_{n+1}-v_n=\frac{{\left(3-v_n\right)}^2}{6-v_n}.$ La suite $\left(v_n\right)$ est-elle monotone ?

Partie B : Recherche de l'expression de la suite

On considère la suite $\left(w_n\right)$ définie pour tout $n$ entier naturel par $w_n=\frac{1}{v_n-3}.$
1. Démontrer que $\left(w_n\right)$ est une suite arithmétique de raison $\left(-\frac{1}{3}\right).$

2. En déduire l'expression de $\left(w_n\right),$ puis celle de $\left(v_n\right)$ en fonction de $n.$

Partie B : Étude mathématique

On définit une suite auxiliaire $\left(v_n\right)$ par : pour tout entier $n⩾1,v_n=n{u}_n-1.$
1. Montrer que la suite $\left(v_n\right)$ est géométrique ; préciser la raison et son premier terme.

2. En déduire que, pour tout entier naturel $n⩾1,$ on a :
$u_n=\frac{1+(0\text{,}5{)}^n}{n}.$

3. Démontrer que, pour tout entier naturel $n⩾1,$ on a :
$u_{n+1}-u_n=-\frac{1+(1+0\text{,}5n)(0\text{,}5{)}^n}{n(n+1)}$.
En déduire le sens de variation de la suite $(u_n)$.

Partie C : Retour à l'algorithmique

En s'inspirant de la partie A, écrire un algorithme permettant de déterminer le plus petit entier $n$ tel que $u_n<0\text{,}001.$