L'eau minérale « Les Deux Montagnes » souhaite actualiser le logo apposé sur ses étiquettes. Elle décide d'opter pour un visuel composé de deux triangles équilatéraux. Les graphistes de la société imposent la contrainte que l'aire totale des deux triangles soit égale à 5 \sqrt{3}. On note \text{M} de coordonnées (x\:; y) un point mobile sur [\mathrm{AB}]. On note \mathrm{A}_{1} et \mathrm{A}_{2} les aires respectives de \text{AMC} et \text{MBD} .

Question préliminaire :
Démontrer que l'aire d'un triangle équilatéral de côté c est donnée par la formule \text{A}=c^{2} \dfrac{\sqrt{3}}{4}.

1. Miranda a décidé de chercher une solution au problème en utilisant un tableur. Elle propose de travailler avec la feuille de calcul ci-dessous.


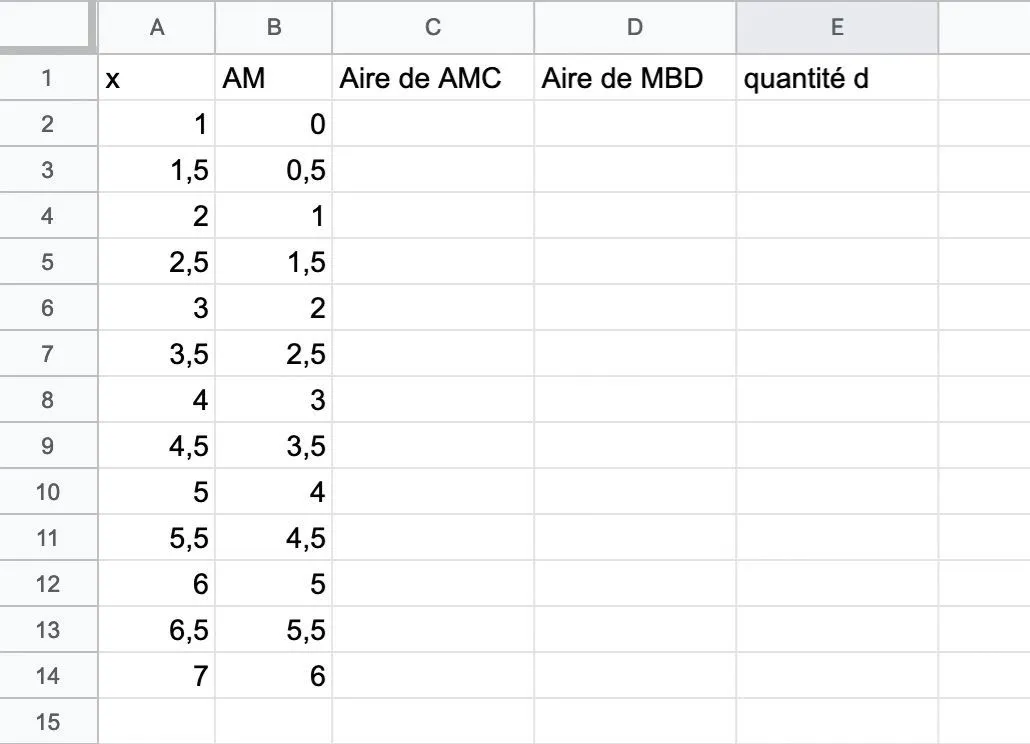
Ouvrir une feuille de calcul et reproduire les deux premières colonnes du tableau proposé par Miranda.

2. Dans quel intervalle \text{I} la variable x varie-t-elle ?

3. Expliciter l'aire \mathrm{A}_{1} du triangle \text{ACM} en fonction de x .

4. Montrer que, pour tout x \in \text{I}, l'aire \mathrm{A}_{2} du triangle \text{MDB} est égale à \dfrac{(7-x)^{2} \sqrt{3}}{4}.

5. En déduire les formules à saisir dans les cellules C2 et D2.

6. Pour répondre aux contraintes, on introduit la quantité d=\text{A}_{1}+\text{A}_{2}-5 \sqrt{3}. Compléter les cellules A2, B2, C2, D2 et E2 avec les bonnes formules puis conclure.

1. a. Ouvrir le logiciel GeoGebra et placer dans un repère orthonormé du plan les points \mathrm{A}(1\:; 3) et \mathrm{B}(7\:; 3).
b. Tracer le segment [\mathrm{AB}].

2. On rappelle que x représente l'abscisse du point \text{M}. Placer un point \text{M} mobile sur le segment [\mathrm{AB}] et construire les deux triangles \text{AMC} et \text{ABD} en utilisant l'outil
3. Ouvrir en parallèle une deuxième fenêtre graphique et créer un point \text{T} de coordonnées \left(x_{\mathrm{T}}\:; y_{\mathrm{T}}\right) tel que x_{\mathrm{T}}=x et y_{\mathrm{T}}=\mathrm{A}_{1}+\mathrm{A}_{2}.

4. Activer la trace du point \text{T} et déplacer le point \text{M} pour visualiser la variation de l'aire des deux triangles en fonction de l'abscisse de \text{T.}

5. En déduire les éventuelles valeurs de x qui satisfont aux contraintes des graphistes.