Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 4
TP / TICE 1
Méthode de Newton
8 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Soit f , la fonction définie sur \R par f(x)=x^{3}-2 x-5.
On appelle \mathcal{C}_f la courbe représentative de la fonction f dans un repère (\text{O}; \vec{i}, \vec{j}).
On admet que l'équation f(x)=0 admet une unique solution \alpha .
On admet que l'équation f(x)=0 admet une unique solution \alpha .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1GeoGebra
1. Conjecturer à quel intervalle d'amplitude 0{,}5 appartient \alpha .
2. À l'aide de GeoGebra, construire \mathcal{C}_f , le point \mathrm{A}_{0} d'abscisse \dfrac{3}{2} de \mathcal{C}_f et tracer la tangente \mathrm{T}_{0} à \mathcal{C}_f en \mathrm{A}_{0}. Elle coupe l'axe des abscisses en un point \mathrm{M}_{0}.
3. \text{A}_{1} est le point de \mathcal{C}_f de même abscisse que \mathrm{M}_{0} et on construit \mathrm{M}_{1} suivant le même procédé.
4. Déterminer une valeur arrondie à 10-1 des abscisses respectives x_0 , x_1 et x_2 de \mathrm{M}_{0}, \mathrm{M}_{1} et \mathrm{M}_{2}.
5. Donner une valeur approchée de \alpha à 10^{-1} près.
2. À l'aide de GeoGebra, construire \mathcal{C}_f , le point \mathrm{A}_{0} d'abscisse \dfrac{3}{2} de \mathcal{C}_f et tracer la tangente \mathrm{T}_{0} à \mathcal{C}_f en \mathrm{A}_{0}. Elle coupe l'axe des abscisses en un point \mathrm{M}_{0}.
3. \text{A}_{1} est le point de \mathcal{C}_f de même abscisse que \mathrm{M}_{0} et on construit \mathrm{M}_{1} suivant le même procédé.
4. Déterminer une valeur arrondie à 10-1 des abscisses respectives x_0 , x_1 et x_2 de \mathrm{M}_{0}, \mathrm{M}_{1} et \mathrm{M}_{2}.
5. Donner une valeur approchée de \alpha à 10^{-1} près.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
1. Vérifier que le point d'intersection \text{M} de \text{T} avec l'axe des abscisses a pour abscisse a-\dfrac{f(a)}{f^{\prime}(a)}.
2. À l'aide d'un tableur, construire un tableau donnant les indices i , les abscisses x_i des points \text{A}_i, les ordonnées y_i des points \text{A}_i et les nombres dérivés f^{\prime}(x_{i}) : on entre 1{,}5 en B2. Quelles formules faut-il entrer en C2, D2 et B3 ?
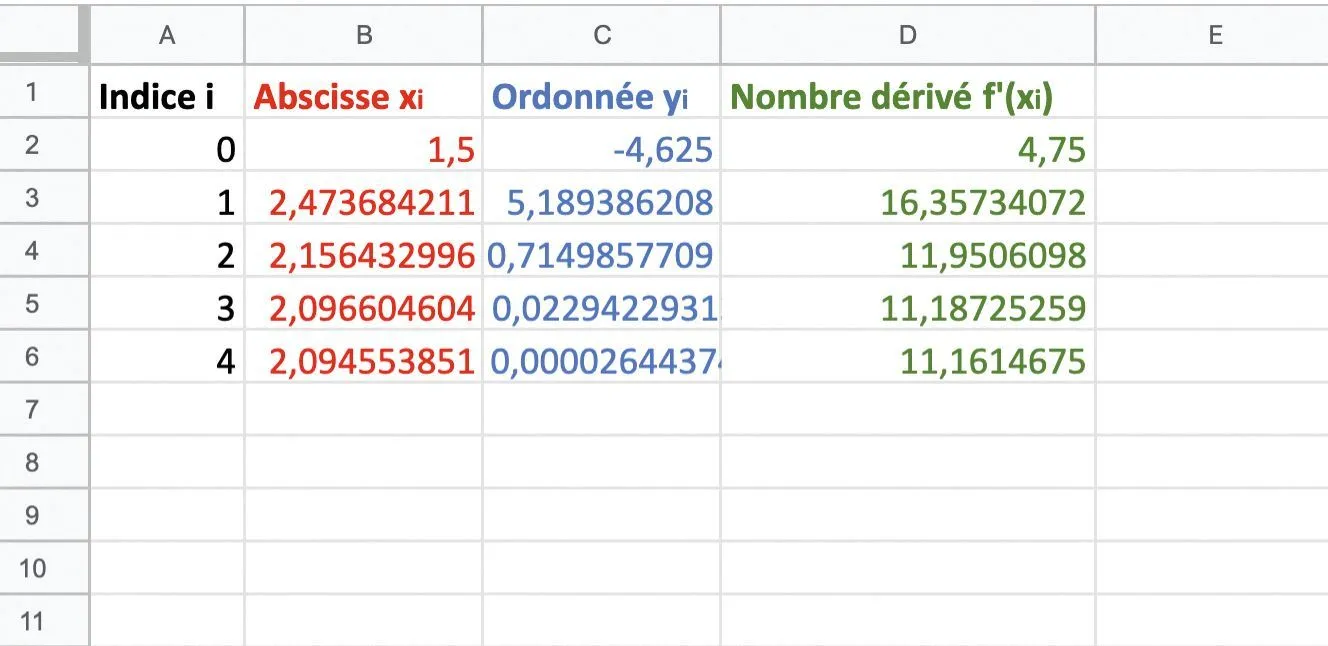
2. À l'aide d'un tableur, construire un tableau donnant les indices i , les abscisses x_i des points \text{A}_i, les ordonnées y_i des points \text{A}_i et les nombres dérivés f^{\prime}(x_{i}) : on entre 1{,}5 en B2. Quelles formules faut-il entrer en C2, D2 et B3 ?
Le zoom est accessible dans la version Premium.
3. Recopier les formules vers le bas et donner une valeur arrondie à 10-7 de \alpha. À son époque, Newton avait trouvé 2,094 551 48.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 3Python
On veut écrire un programme sous Python qui retourne sous forme de liste les différentes valeurs x_{0}, x_{1}, \ldots, x_{n} pour une valeur de x_0 et une valeur
de n données.
1. Écrire sous Python deux fonctions, l'une qui retourne f(x) et l'autre qui retourne f^{\prime}(x).
2. Compléter la fonction \bf{newton} qui calcule x_0 ,
x_1 , ... , x_n pour une valeur de x_0 et une valeur de n données.
3.
Comment utiliser la fonction \bf{affichage} avec la fonction newton pour qu'elle affiche les cinq premières valeurs approchées de la solution de l'équation f(x)=0\:?
1. Écrire sous Python deux fonctions, l'une qui retourne f(x) et l'autre qui retourne f^{\prime}(x).
def f(x):
return(...)
def f_prime(x):
return(...)
def newton(x_0, nb_etapes):
valeurs = [0]*(nb_etapes + 1) #de 0 à nb_etapes
valeur[0] = ...
for idValeur in range(... , ...):
x = ...
valeurs[idValeur] = x - ...
return(valeurs)
def affichage(liste):
n = len(liste) #nombre d'éléments dans la liste
for idValeur in range(n):
print("x_{} = {}".format(idValer, liste[idValeur]))
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
L'équation de ce TP a été étudiée par Isaac Newton dans son livre La méthode des fluxions, et les suites infinies (1736).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Obtenir des valeurs approchées de \alpha en utilisant une des trois méthodes.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah