Pour s'échauffer - Pour commencer

On s'intéresse à l'astéroïde Rhea Sylvia décrivant une orbite elliptique autour du Soleil selon le schéma ci‑contre.

1. Justifier la position du Soleil indiquée sur le schéma ci‑dessus en citant la loi de Kepler utilisée.

2. On suppose que les durées de parcours entre les points ${\text{M}}_1$ et ${\text{M}}_1{}^{\prime }$, puis ${\text{M}}_2$ et ${\text{M}}_1{}^{\prime }$ sont égales. En utilisant une des lois de Kepler, donner la relation existant entre les aires $A_1$ et $A_2$.

✔ APP : Faire un schéma

La comète de Encke est la seconde comète périodique découverte en 1786 après celle de Halley. Elle possède une période de révolution $T_{\mathrm{H}}=3,3$ a. Tout comme les autres objets célestes du système solaire, elle gravite autour du Soleil selon une orbite elliptique.

Lors de sa mission d'exploration, la sonde européenne Cassini‑Huygens a livré les premiers clichés de Saturne, noté $\text{S}$, de ses anneaux et de ses nombreux satellites, dont Titan, noté $\text{T}$, le plus grand, de masse $M.$ On considérera que son centre décrit une trajectoire circulaire autour de Saturne.

1. Représenter qualitativement sur un schéma Saturne, Titan et la force de gravitation appliquée sur Titan.

Insérer une formule mathématique

2. Donner l'expression vectorielle de cette force.

Insérer une formule mathématique

3. Exprimer l'accélération vectorielle de Titan en précisant la loi utilisée. Préciser ses caractéristiques.

Insérer une formule mathématique

4. Montrer que le mouvement de Titan est uniforme.

Insérer une formule mathématique

5. Montrer que l'expression de la vitesse orbitale de Titan autour de Saturne est $v_{\mathrm{T}}=\sqrt{\frac{G\cdot M_{\mathrm{S}}}{r_{\mathrm{T}}}}$. Calculer sa valeur.

Insérer une formule mathématique

Constante de gravitation universelle : $G=6,67\times 10^{-11}$ m³·kg-1·s^-2

Rayon de l'orbite de Titan : $r_{\text{T}}=1,22\times 10^6$ km

Rayon de Saturne : $R_{\text{S}}=5,8\times 10^4$ km

Masse de Saturne : $M_{\text{S}}=5,69\times 10^{26}$ kg

La Station spatiale internationale est occupée en permanence depuis sa mise en place en 1998. Elle est consacrée à la recherche scientifique dans l'environnement spatial. Elle se déplace à une altitude moyenne de 400 km au‑dessus de la surface de la Terre.

1. Calculer la distance parcourue par la station au cours d'une seule révolution autour de la Terre.

Insérer une formule mathématique

2. En déduire la période de révolution de la station si sa vitesse moyenne est environ $V_{\mathrm{ISS}}=27600$ km·h^-1.

Insérer une formule mathématique

Rayon de la Terre : $R_{\text{T}}=6370$ km

✔ REA : Utiliser un modèle

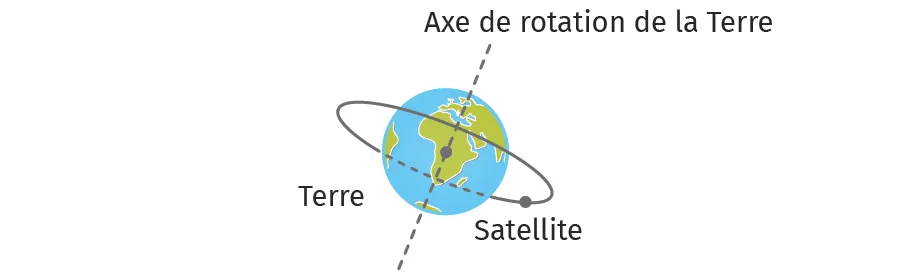
Le satellite Alphasat a été mis en orbite géostationnaire par la société Arianespace depuis Kourou en 2013. Il a pour but d'assurer des missions de télécommunications. Il se déplace suivant une trajectoire supposée circulaire de rayon $r$ et possède une masse $m$.

1. Expliquer ce qu'est un satellite géostationnaire.

Insérer une formule mathématique

2. Préciser le référentiel le plus adapté pour étudier le mouvement du satellite, assimilé à un point ponctuel $\text{S}$.

Insérer une formule mathématique

3. Dans le repère de Frenet, retrouver l'expression du vecteur accélération ${\overrightarrow{a}}_{\mathrm{s}}$ de $\text{S}$ tel que sa valeur est égale à $a_{\text{s}}=G\cdot \frac{M_{\text{T}}}{r^2}$.

Insérer une formule mathématique

Les surveillances de la prévision à court terme et de l'évolution du climat sont notamment assurées par les satellites météorologiques NOAA et Meteosat. On suppose qu'ils gravitent autour de la Terre en orbite circulaire avec une période de révolution d'environ $1440$ min pour Meteosat et $100$ min pour NOAA.

1. Rappeler la propriété principale d'un satellite géostationnaire.

Insérer une formule mathématique

2. Rappeler la période moyenne de rotation de la Terre.

Insérer une formule mathématique

3. En déduire lequel des deux satellites peut être considéré comme géostationnaire.

Insérer une formule mathématique

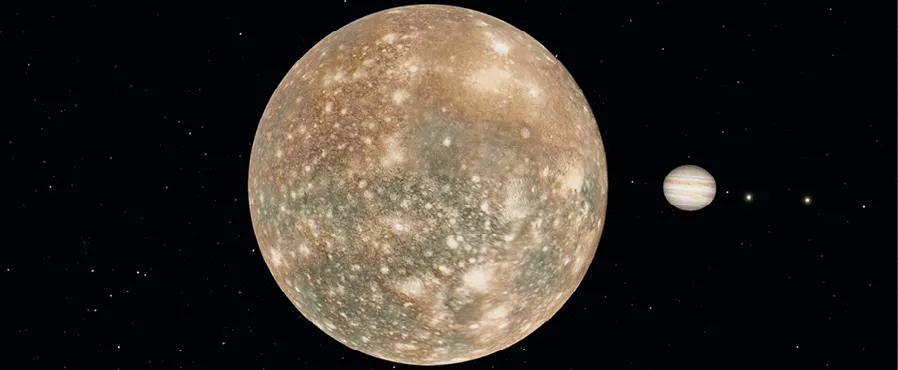
Avec Io, Callisto fait partie des satellites naturels de Jupiter que Galilée a observés en 1610. Io gravite autour de Jupiter à une distance $r_{\mathrm{Io}}=4,0\times 10^5$ km avec une période de révolution $T_{10}=1,5$ j.

Déterminer la période de révolution de Callisto sachant qu'elle est 4,5 fois plus éloignée de Jupiter que Io.

Hermione est un astéroïde qui gravite autour de son astre attracteur à une distance $r_H=3,45$ u.a. avec une période de révolution de $6,398$ a.

1. Montrer que $\frac{T^2}{r^3}=3,0\times 10^{-19}$ s² ·m^-3 à l'aide du doc.

2. Déterminer le rapport $\frac{T^2}{r^3}$de l'astéroïde Hermione.

3. En déduire si Hermione gravite autour du Soleil.

L'astéroïde Toutatis est considéré comme un géocroiseur, car son orbite est régulièrement proche de celle de la Terre. Sa distance moyenne au Soleil est égale à $2,52$ u.a. pour une période de révolution de $4,01$ a.

1. Comparer le rapport $\frac{T^2}{r^3}$ du géocroiseur Toutatis avec le coefficient directeur de la droite $T^2=f\left(r^3\right)$ du doc.

2. En déduire si Toutatis fait partie du système solaire.