Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 10
Activités
Configurations géométriques
13 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AUne nouvelle équation : celle du cercle
Objectif : Déterminer une équation d'un cercle dans un repère orthonormé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
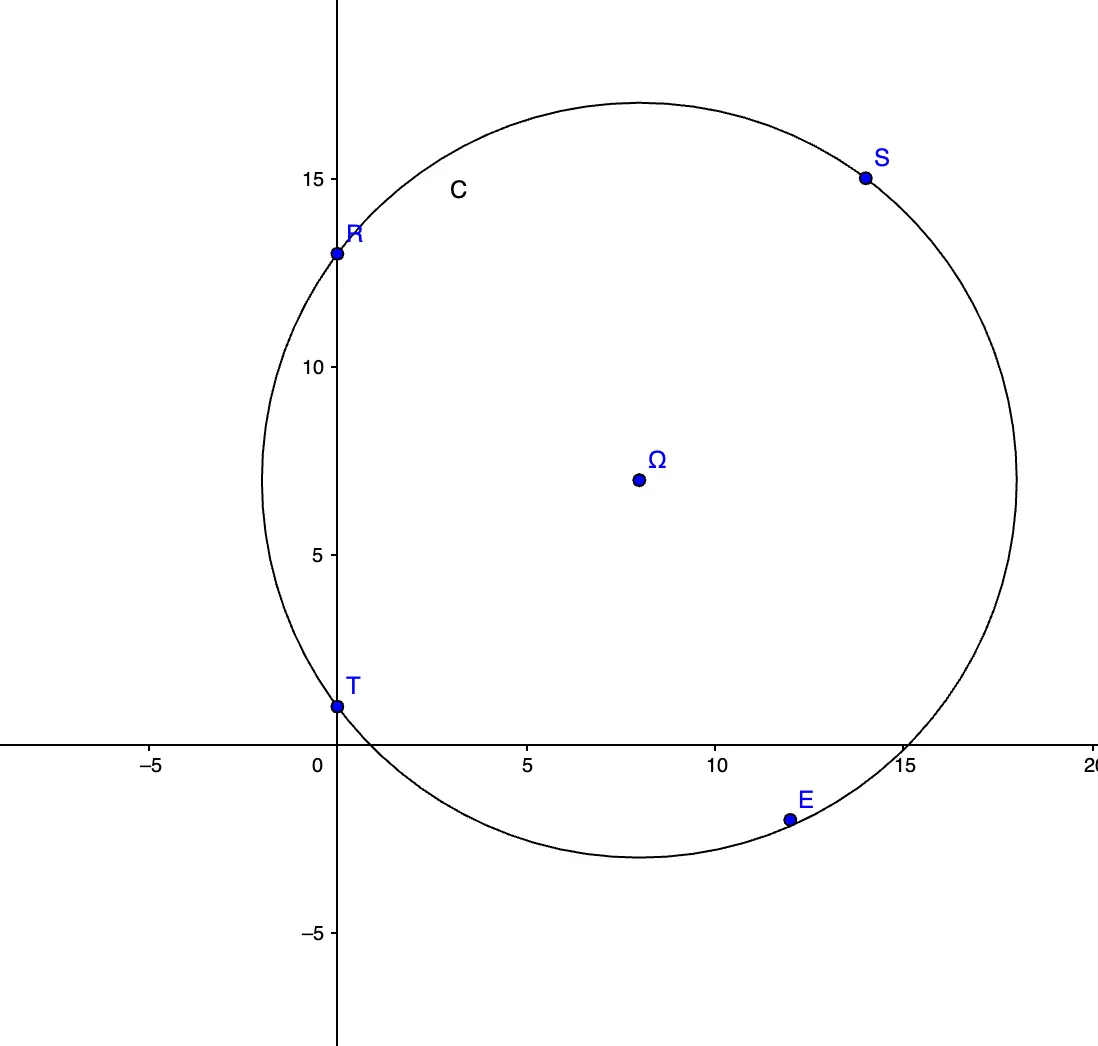
Dans ce repère orthonormé, on considère le cercle \mathcal{C} de centre \Omega et qui passe par \text{R.}
On se propose de déterminer si un point appartient à ce cercle ou non.
On se propose de déterminer si un point appartient à ce cercle ou non.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
À l'aide d'un logiciel de géométrie ou à la main, reproduire la représentation ci-contre et placer les points au fur et à mesure de l'activité. Les points notés ont des coordonnées entières.
GeoGebra
Cliquez pour accéder à une correction
Le zoom est accessible dans la version Premium.
2
Déterminer la valeur exacte du rayon du cercle \mathcal{C}.
3
a) Quelles sont les coordonnées des points \text{S} et \text{T} ?
b) Ces points appartiennent-ils à \mathcal{C} ?
c) Le point \text{E}(12\: ; - 2) appartient-il à \mathcal{C} ?
4
On note \text{M} le point de coordonnées (x \:; y) dans ce même repère orthonormé.
a) Donner une condition pour que le point \text{M} appartienne au cercle \mathcal{C}.
b) Calculer la longueur \Omega\text{M} en fonction des coordonnées de \text{M.}
c) En déduire une expression en fonction de x et y qui détermine l'ensemble des points du cercle.
Logique
Si deux longueurs sont égales alors leur carré l'est aussi.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BilanDonner une équation d'un cercle de centre \Omega(a \: ; b) et de rayon r dans un repère orthonormé.
Bilan
Donner une équation d'un cercle de centre \Omega(a \: ; b) et de rayon r dans un repère orthonormé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BÀ la découverte d'une nouvelle formule
Objectif : Démontrer une formule en lien avec les médianes dans un triangle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On se place dans un triangle \text{ABC} quelconque et on note \text{M} le pied de la médiane issue de \text{A} et \text{H} celui de la hauteur issue de \text{A.} On pose \text{HM} = x .
On souhaite démontrer la formule suivante, appelée formule de la médiane : \mathrm{AB}^{2}+\mathrm{AC}^{2}=2 \mathrm{AM}^{2}+\dfrac{1}{2} \mathrm{BC}^{2}.
On souhaite démontrer la formule suivante, appelée formule de la médiane : \mathrm{AB}^{2}+\mathrm{AC}^{2}=2 \mathrm{AM}^{2}+\dfrac{1}{2} \mathrm{BC}^{2}.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
a) À l'aide d'un logiciel de géométrie dynamique ou à la main, représenter la figure ci-contre.
GeoGebra
Cliquez pour accéder à une correction
Le zoom est accessible dans la version Premium.
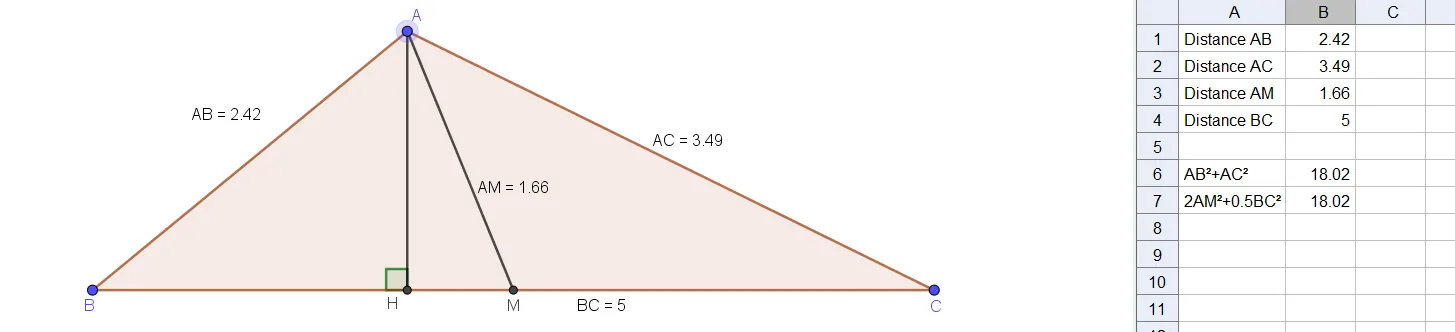
b) Lire graphiquement, ou en mesurant, les longueurs \text{AB,} \text{AC,} \text{BC} et \text{AM} et constater que la relation ci-dessus est vérifiée.
2
Dans cette question, on pose \text{AH} = 2 et \text{BM} = \text{MC} = 3 .
a) Exprimer \text{AB}^2, \text{AC}^2 et \text{AM}^2 en fonction de x .
b) Calculer \text{BC}^2.
c) Vérifier que \mathrm{AB}^{2}+\mathrm{AC}^{2}=2 \mathrm{AM}^{2}+\dfrac{1}{2} \mathrm{BC}^{2}.
3
Dans cette question, on pose \text{AH} = h et \text{BM} = \text{MC} = a où h et a sont deux réels strictement positifs.
a) Montrer que \mathrm{AB}^{2}=(a-x)^{2}+h^{2} et que \mathrm{AC}^{2}=(a+x)^{2}+h^{2}.
b) Exprimer \text{AM}^2 en fonction de x et de h.
c) Calculer \text{BC}^2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BilanDans le cas général, vérifier alors que \mathrm{AB}^{2}+\mathrm{AC}^{2}=2 \mathrm{AM}^{2}+\dfrac{1}{2} \mathrm{BC}^{2}.
Bilan
Dans le cas général, vérifier alors que \mathrm{AB}^{2}+\mathrm{AC}^{2}=2 \mathrm{AM}^{2}+\dfrac{1}{2} \mathrm{BC}^{2}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CLieu de points
Objectif : Trouver le lieu géométrique de points vérifiant une propriété géométrique donnée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On appelle lieu géométrique un ensemble de points vérifiant tous la même propriété géométrique. Par exemple, la médiatrice d'un segment est l'ensemble des points situés à égale distance des extrémités de ce segment : il s'agit bien d'un lieu géométrique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Un métallurgiste possède une plaque de cuivre de forme triangulaire. Il veut la découper de façon à avoir six plaques triangulaires de même surface.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Dans un triangle, on rappelle que la médiane issue d'un sommet est la droite qui passe par ce sommet et par le milieu du côté opposé.
a) Tracer un triangle \text{ABC} non plat et non isocèle en \text{A} ainsi que la hauteur et la médiane issues de \text{A.} On note \text{H} le pied de la hauteur et \text{A'} le milieu de \text{[BC].}
Cette fonctionnalité est accessible dans la version Premium.
b) Donner une formule de l'aire du triangle \text{ABC} ainsi que celle des triangles \text{ABA}' et \text{AA}'\text{C.}
c) Quelle relation existe-t-il entre ces aires ? Justifier.
2
a) Placer maintenant un point \text{M} à l'intérieur du triangle \text{ABC} et tracer les droites \text{(AM),} \text{(BM)} et \text{(CM).}
Cette fonctionnalité est accessible dans la version Premium.
b) En combien de triangles de sommet \text{M} la figure a-t-elle été divisée ?
c) Justifier que les triangles \text{AA}'\text{B} et \text{AA}'\text{C} ont la même aire.
d) Si \text{M} se situe sur la médiane issue de \text{A,} que dire des triangles \text{MA}'\text{B} et \text{MA}'\text{C} ? Et des triangles \text{MAB} et \text{MAC} ?
3
a) À l'aide de GeoGebra, faire la figure ci‑après et afficher les aires des six triangles constitués de sommet \text{M.}
Le zoom est accessible dans la version Premium.
GeoGebra
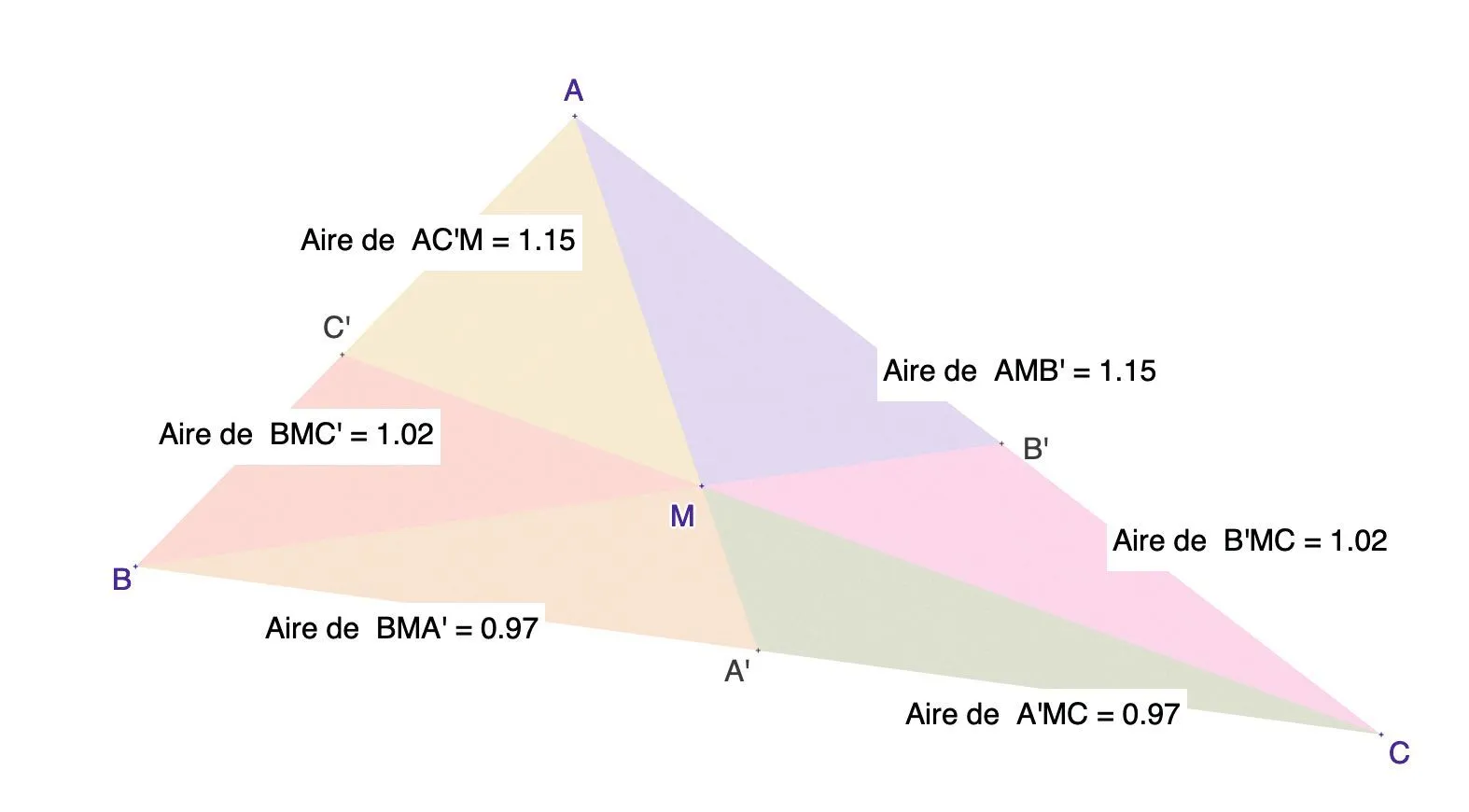
Cliquez pour accéder à une correction
Le zoom est accessible dans la version Premium.
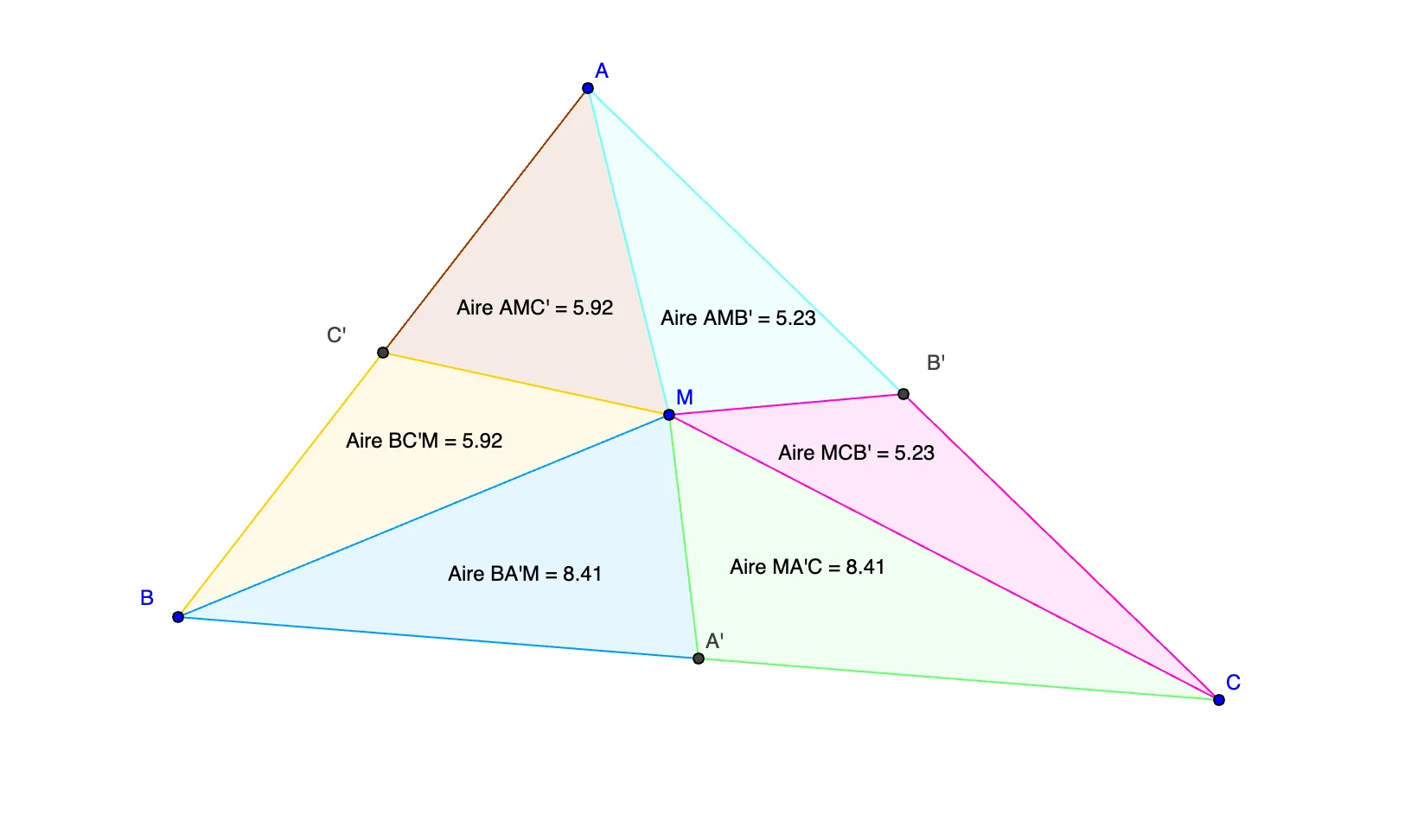
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BilanOù placer le point \text{M} pour que les six triangles aient la même aire ?
Bilan
Où placer le point \text{M} pour que les six triangles aient la même aire ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah