Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 1
Activités
Suites numériques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ASoyons explicites
Objectif : Utiliser un tableur pour introduire et définir une suite de manière explicite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On souhaite introduire la notion de suite à l'aide d'un tableur afin de pouvoir trouver une expression du terme général en fonction de n. On considère la feuille de calcul suivante.
Le zoom est accessible dans la version Premium.
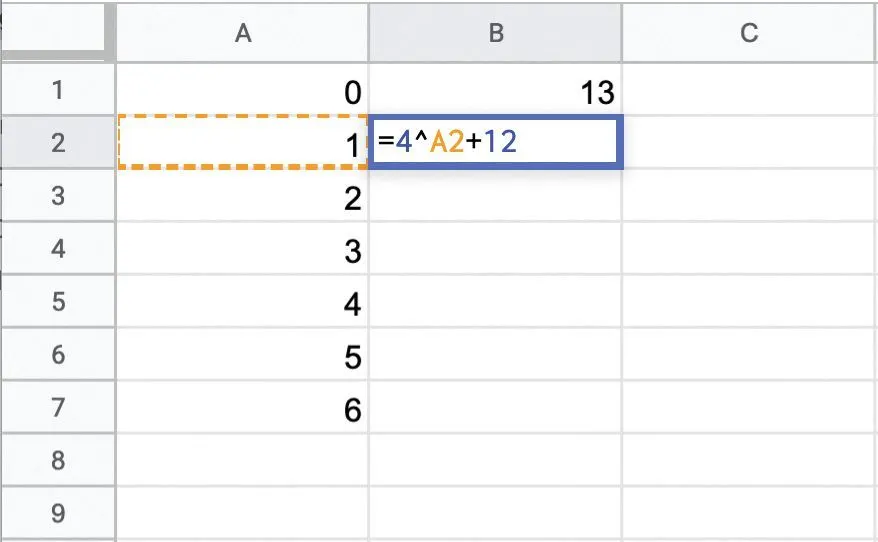
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Quel résultat sera affiché dans la cellule B2 ?2
On étend la formule de la cellule B2 jusqu'à la cellule B100. On complète également la colonne A. Quelle est la valeur affichée en cellule B5 ?3
Pour tout entier n, on note u_n la valeur affichée en cellule B(\mathbf{n+ 1} ) .a) Dans quelle cellule est affichée u_0 ? Quelle est sa valeur ?
b) Mêmes questions avec u_1, u_{49} puis u_{99}.
4
Exprimer u_n en fonction de n pour tout entier n.Remarque
On dit alors que la suite (u_n) est définie de manière explicite ; autrement dit, directement en fonction de n.5
On souhaite utiliser la colonne C pour calculer le nombre (n + 1)^4 pour chaque entier n de 0 à 99.a) Quel sera le résultat pour n = 0 ? n = 4 ? n = 10 ?
b) Quelle formule doit-on écrire en cellule C1 puis recopier jusqu'en cellule C100 pour obtenir les 100 premiers termes de cette suite ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan
Comment définir une suite de manière explicite ? Quel est le lien avec la notion de fonction apprise en seconde ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BUn travail récurrent
Objectif : Utiliser un algorithme pour introduire et définir une suite par récurrence.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On souhaite introduire la notion de suite définie par récurrence à l'aide du programme de calcul ci‑après.
\boxed{
\begin{array} { l } { \text {Étape 1 : Prendre un nombre.}} \\
\text {Étape 2 : Le multiplier par 2.} \\
\text {Étape 3 : Ajouter 10.} \\
\end{array}
}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Appliquer le programme de calcul pour le nombre 3.2
Appliquer de nouveau le programme au résultat obtenu précédemment.On continue d'appliquer ce programme à chaque nouveau résultat pour obtenir une suite de nombres. Pour tout entier n supérieur ou égal à 1, on note v_n le nombre obtenu lors de l'application du programme au n-ième résultat. On pose v_0 =3 et on obtient alors v_1 =16.
3
Quelle est la valeur de v_2 et celle de v_3 ?4
a) Quelle formule permet de passer de v_1 à v_2 ? Et de v_2 à v_3 ?b) Pour tout entier n, exprimer v_{n+1} en fonction de v_n.
5
Combien de termes faut-il calculer pour déterminer la valeur de v_{100} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan Que signifie « définir une suite par récurrence » ? Quelle différence principale y a-t-il avec les suites définies explicitement ?
Bilan
Que signifie « définir une suite par récurrence » ? Quelle différence principale y a-t-il avec les suites définies explicitement ?Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CSuites arithmétiques et géométriques
Objectif : Introduire et utiliser les suites arithmétiques et géométriques.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans le film de science fiction Time Out se déroulant en 2169, le temps est la nouvelle unité monétaire. Dans ce contexte, un étudiant souhaite trouver un travail pour le mois d'août, deux contrats lui sont proposés :
A : 10 000 secondes le premier jour puis une augmentation de 10 000 secondes supplémentaires par jour.
B : 2 secondes le premier jour et le salaire multiplié par 2 chaque jour.
A : 10 000 secondes le premier jour puis une augmentation de 10 000 secondes supplémentaires par jour.
B : 2 secondes le premier jour et le salaire multiplié par 2 chaque jour.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Estimer, sans calcul, le meilleur contrat pour cet étudiant.2
On s'intéresse au premier contrat.a) Combien gagnerait-il le 1er août ? Le 2 août ? Le 3 août ?
b) Quelle somme totale aura-t-il gagnée après trois jours de travail ?
c) On note u_n le montant gagné au jour n du mois d'août.
Exprimer les résultats de la question
2
a) en utilisant la notation u_n.d) Justifier que, pour tout entier n \ne 0, u_n = 10\, 000n.
Remarque
On dit alors que la suite (u_n) est une suite arithmétique de raison 10\,000 et de premier terme u_1 =10\,000.3
On s'intéresse maintenant au second contrat.a) Combien gagnerait-il le 1er août ? Le 2 août ? Le 3 août ?
b) Quelle somme totale aura-t-il gagnée après trois jours de travail ?
c) On note v_n le montant gagné au jour n du mois d'août.
Exprimer les résultats de la question
3
a) en utilisant la notation v_n.
d) Justifier que, pour tout entier n \ne 0, v_n = 2^n.
a) Que représente cette somme ?
b) Montrer que S = 10\, 000 (1 + 2 + ... + 31).
c) On note S' = 1 + 2 + ... + 31. En remarquant que S' = 31 + 30 + ... + 1, montrer que 2S' = 31 \times 32.
d) En déduire la valeur de S' puis celle de S.
a) Que représente cette somme ?
b) Montrer que 2T = v_2+v_3+....+v_{31}+2^{32}.
c) Calculer alors 2T - T pour en déduire la valeur de T.
Remarque
On dit que la suite (v_n) est une suite géométrique de raison 2 et de premier terme v_1 = 2.4
On pose S = u_1+u_2+....+u_{31}. a) Que représente cette somme ?
b) Montrer que S = 10\, 000 (1 + 2 + ... + 31).
c) On note S' = 1 + 2 + ... + 31. En remarquant que S' = 31 + 30 + ... + 1, montrer que 2S' = 31 \times 32.
d) En déduire la valeur de S' puis celle de S.
5
On pose T= v_1+v_2+....+v_{31}. a) Que représente cette somme ?
b) Montrer que 2T = v_2+v_3+....+v_{31}+2^{32}.
c) Calculer alors 2T - T pour en déduire la valeur de T.
6
Quel contrat l'étudiant doit-il choisir ?Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan Comment définir une suite arithmétique et une suite géométrique ? Pour chaque suite, quelle formule permet de calculer la somme des premiers termes ?
Bilan
Comment définir une suite arithmétique et une suite géométrique ? Pour chaque suite, quelle formule permet de calculer la somme des premiers termes ?Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah