Méthode de Monte-Carlo

On considère l'aire du domaine hachuré ci-contre, délimité par les droites d'équations y = 0, x = 0 , x = 1 et l'arc de parabole d'équation y = x^{2}. Archimède a montré dans La Quadrature de la parabole que l'aire de ce domaine est exactement \dfrac{1}{3} mais aucune formule en classe de première ne permet de la déterminer. On admet que la probabilité qu'un point choisi aléatoirement dans le carré appartienne au domaine hachuré est proportionnelle à l'aire de ce dernier.

Question préliminaire : Déterminer un encadrement de l'aire du domaine hachuré.

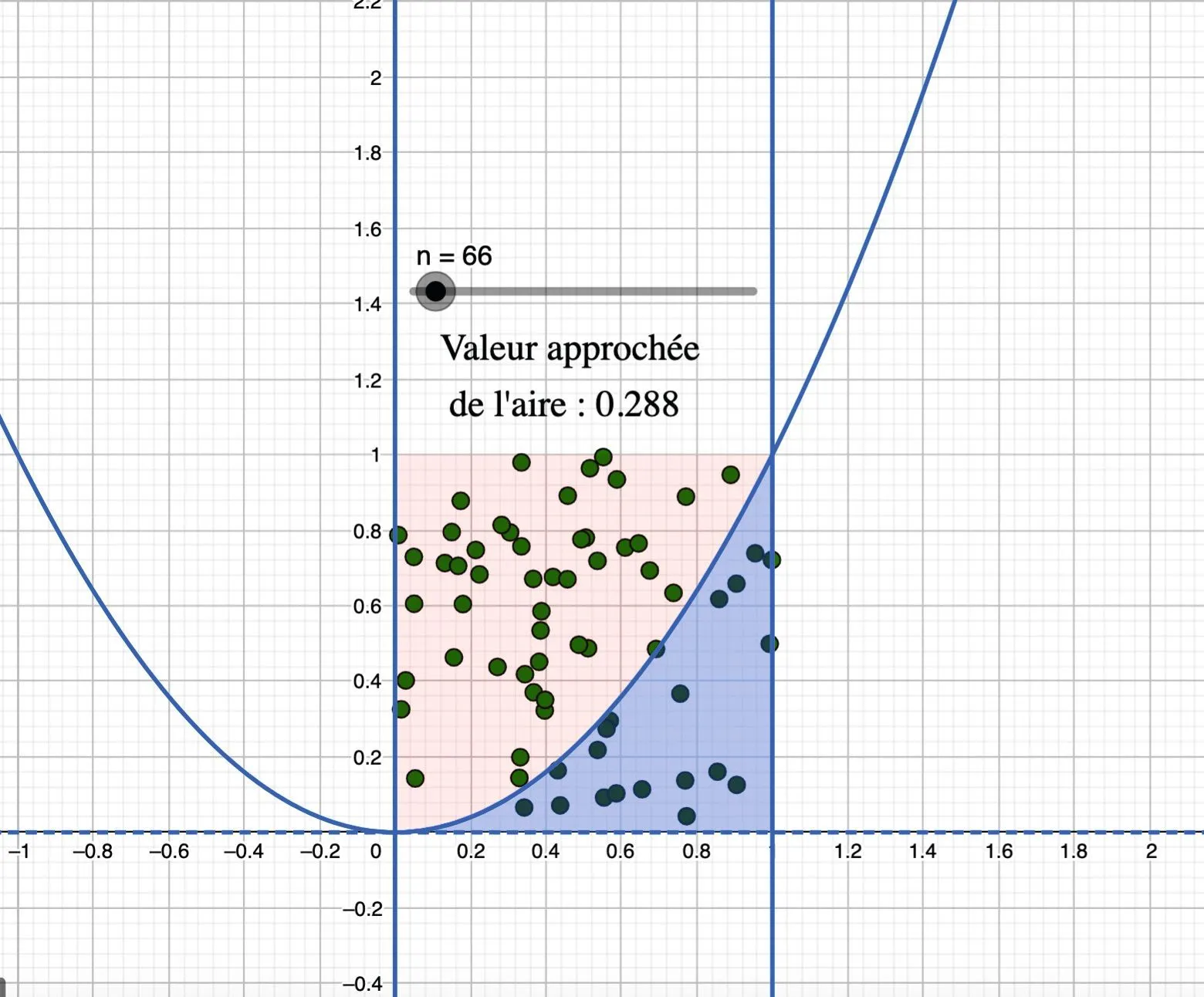
1. Créer le domaine dans une fenêtre graphique de GeoGebra.
2. Créer un curseur n qui prend des valeurs entières de 1 à 1\,000.
3. a. L'instruction random() permet d'avoir un nombre aléatoire entre 0 et 1. Où se situe un point \text{A} créé avec la saisie A = (random(), random()) ?

b. On souhaite créer une liste de n points placés aléatoirement dans le carré. Comment compléter la saisie suivante pour obtenir ce que l'on souhaite ?

4. La région du plan hachurée est délimitée par les valeurs de x comprises entre 0 et 1.
a. Donner un encadrement de y en fonction de x .

b. Le symbole && signifie « et » dans GeoGebra. Comment compléter la saisie suivante pour colorier la région qui nous intéresse ?

5. Que signifie la saisie suivante ?

6. En saisissant S = Somme[Liste2], on obtient le nombre de points situés dans la région hachurée. Que faut-il saisir pour avoir la proportion de points dans la région hachurée par rapport à l'ensemble des points ?

7. Faire varier la valeur de n et conclure.

En utilisant Python, on va placer aléatoirement 1 000 points dans le carré puis déterminer l'aire du domaine hachuré.

1. Importer le module random avec l'instruction from random import*.
2. De quelle manière est définie la variable a ci-dessous ?

3. Créer deux variables xA et yA de telle façon qu'elles définissent les coordonnées d'un point \text{A} placé aléatoirement dans le carré défini dans l'introduction.

4. Quelle instruction doit-on saisir pour vérifier que le point \text{A} est situé dans le domaine hachuré ?